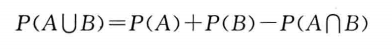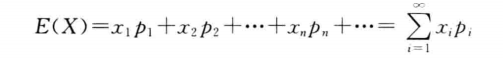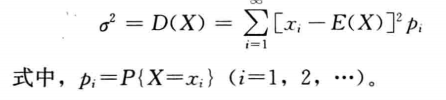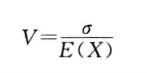随机事件与概率
事件
- 偶然事件: 同一次实验中,可能出现也可能不出现的的时间叫做偶然事件
- 必然事件:同一次实验中,一定出现的事件叫做必然事件
- 不可能事件: 同一次实验中,一定不出现的事件叫做必然事件
- 基本事件: 如果一个事件不能分解成多个事件,那么称其为基本事件
概率
事件A的概率是事件A在实验中出现的可能性的度量,其大小记做P(A),P(A)为时间A的概率
- 古典概率定义

- 统计学概率定义
概率性质与运算法则
概率基本性质
概率加法法则
- 两个互斥事件的概率为两个事件的概率和
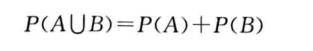
- 对于任意两个随机事件他们和的概率为两个事件的概率和减去两个事件的相交概率
条件概率
当某一个事件B已经发生的时候,事件A发生的概率,称为事件B发生的条件下,事件A发生的条件概率,记做,**P(A|B)**, 一般 **P(A|B)!= P(A)**
乘法公式

- 乘法公式
**P(AB) = P(A) * P(B|A)****P(BA) = P(AB)**
独立性
如果事件A和事件B独立,即事件A或B发生都不会影响另一方发生的概率**P(AB) = P(A) * P(B)**
互斥和独立
离散型随机变量和概率分布
随机变量概念
两种类型的随机变量
通常可以分为,
- 离散型随机变量

- 连续型随机变量
离散型随机变量概率分布
离散型随机变量的期望值和方差
期望值
方差和标准差
标准差
离散系数
二项分布和泊松分布
二项分布
实际问题中,有许多问题只包含两种结果,这种随机变量服从的概率分布成为二项分布,这些事件的共同性质如下,
- 包含了n个相同的实验
- 每次只有两种可能的结果
- 出现“成功”的概率,每次实验都是一致的
- 实验是相互独立的
- 实验“”成功”或者“失败”是可以计数的
泊松分布
泊松分布是用来描述在一定时间范围内,指定面积或体积内某时间内某时间发生次数的分布
如,
公式如下,
在n重复贝努力实验中,当成功的概率很小,试验次数很大时,二项分布可以近似等于泊松分布, 实际应用中,满足以下条件即可:
p <= 0.25 , n > 20, np <= 5, 可以用泊松分布近似表示二项分布连续型随机变量分布
由于连续型随机变量可以取某一区间的任意值,无法像离散型随机变量那样全部列出每个值对应的概率,因此通常用数学函数的形式和分布函数的形式描述,当用f(x)表示连续型随机变量的时候,将f(x)称为概率密度函数,其应该满足如下条件,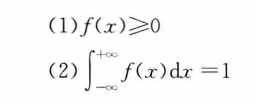
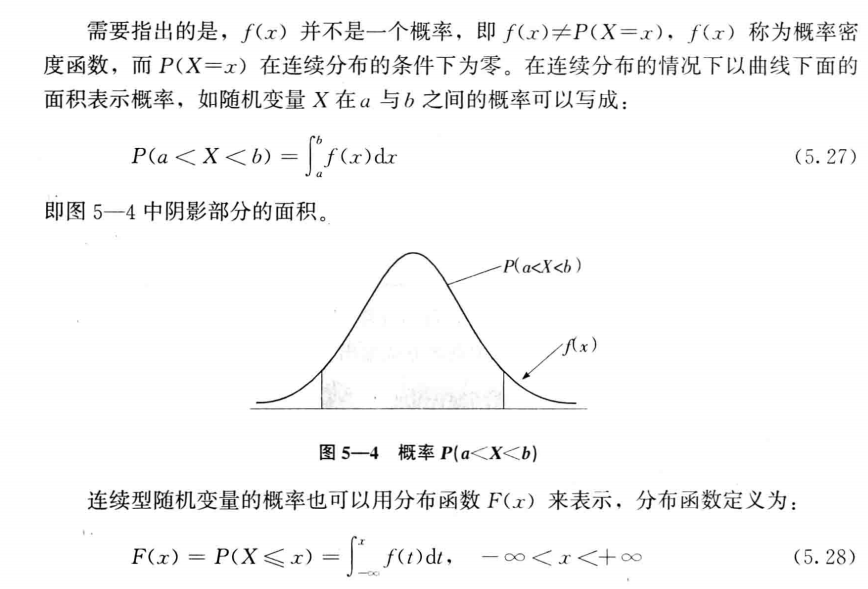


均匀分布
概率密度函数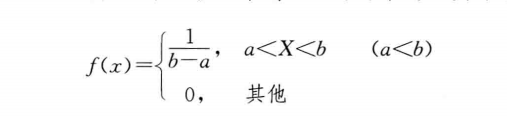
E(X) = 1/2 * (a + b)D(X) = (b - a)^2 / 12指数分布
概率密度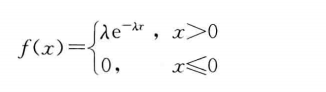
E(X) = 1/λ^2D(X) = 1/λ^2正态分布
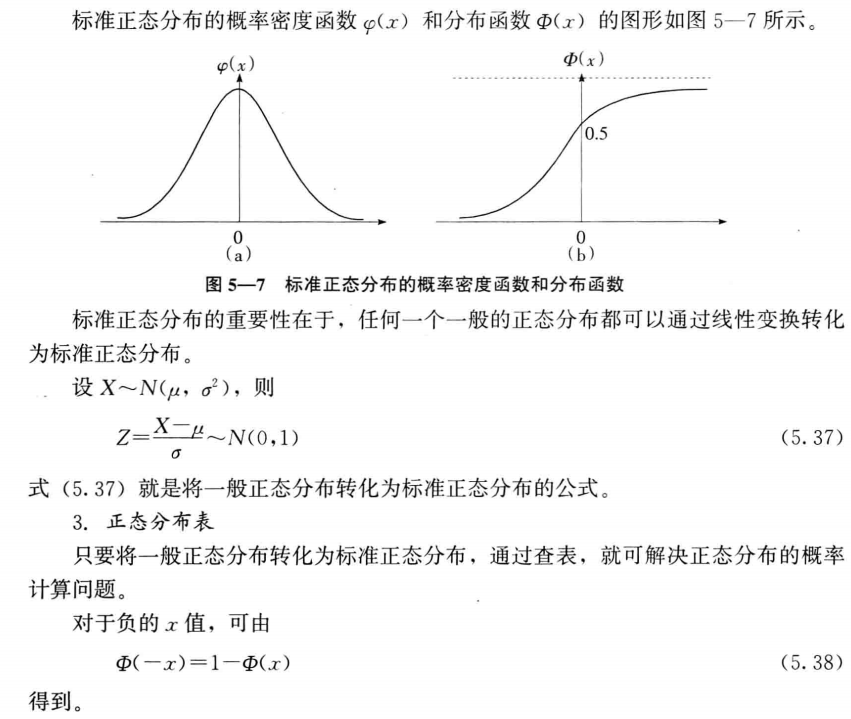
正态分布是一种具有钟型概率密度分布的随机变量,相应的概率分布称为正态分布, 如下图,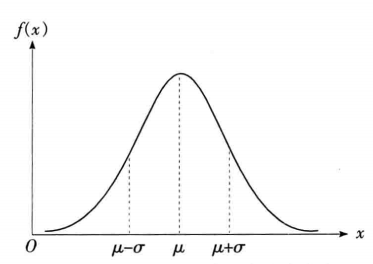
概率密度函数为: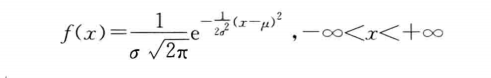

正态分布的性质
如下图,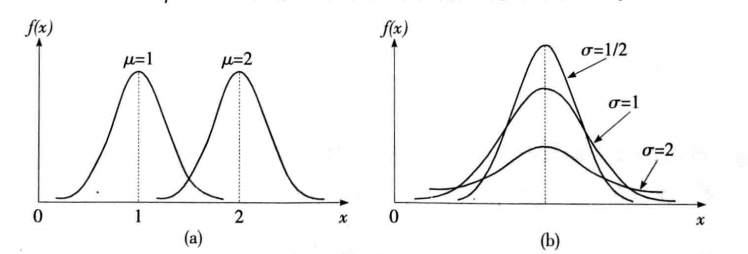
标准正态分布