二叉堆本质上是一种完全二叉树，它分为两个类型。

  1. 最大堆：最大堆的任何一个父节点的值，都大于或等于 它左、右孩子节点的值。

  2. 最小堆：最小堆的任何一个父节点的值，都小于或等于 它左、右孩子节点的值。

    二叉堆的自我调整

    对于二叉堆，有如下几种操作。

  3. 插入节点。

  4. 删除节点。
  5. 构建二叉堆。

这几种操作都基于堆的自我调整。所谓堆的自我调整，就是把一个不符合堆性质的完全二叉树，调整成一个堆。下面让我们以最小堆为例，看一看二叉堆是如何进行自我调整的。

1.插入节点

当二叉堆插入节点时，插入位置是完全二叉树的最后一个位置。例如插入一个新节点，值是 0。
image.png
这时，新节点的父节点 5 比 0 大，显然不符合最小堆的性质。于是让新节点“上浮”，和父节点交换位置。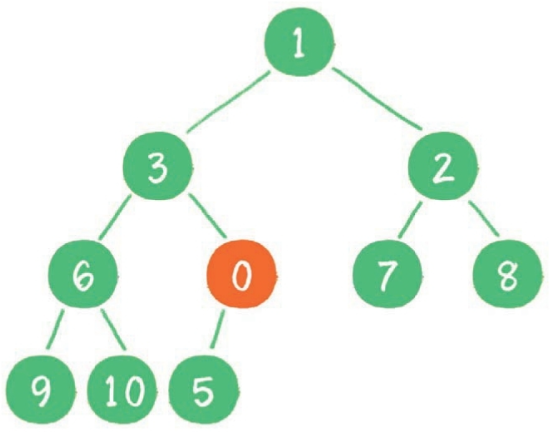
image.png
继续用节点 0 和父节点 3 做比较，因为 0 小于 3，则让新节点继续“上浮”。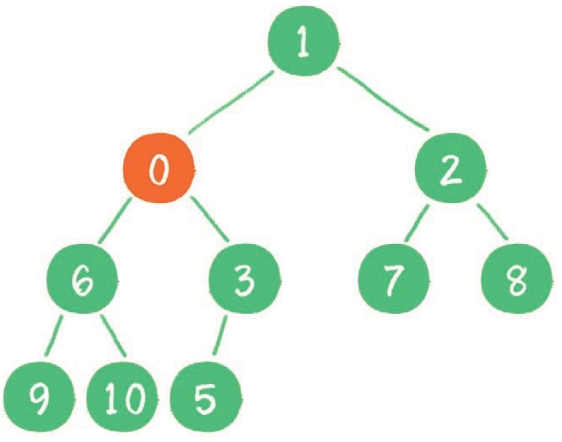
image.png
继续比较，最终新节点 0“上浮”到了堆顶位置。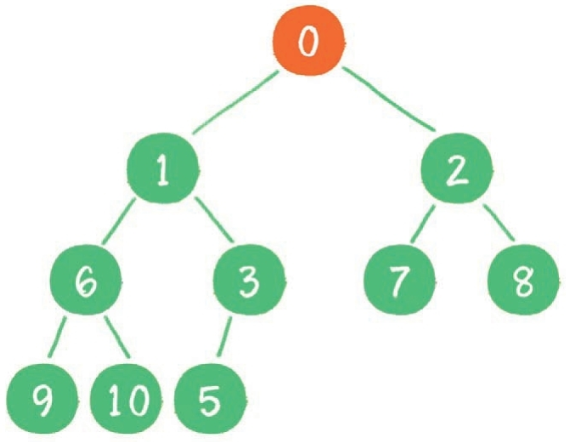
image.png

2.删除节点

二叉堆删除节点的过程和插入节点的过程正好相反，所删除的是处于堆顶的节点。例如删除最小堆的堆顶节点 1。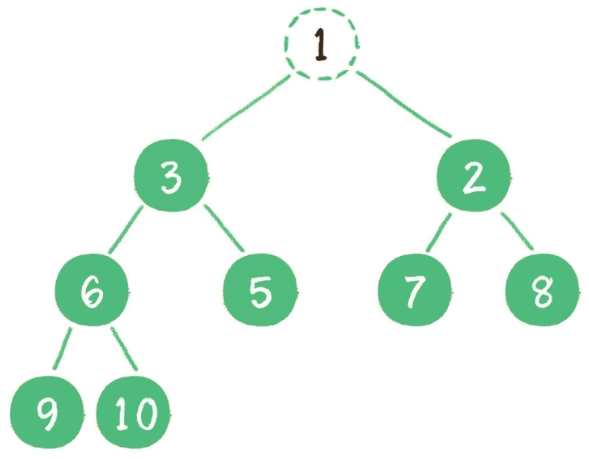
image.png
这时，为了继续维持完全二叉树的结构，我们把堆的最后一个节点 10 临时补到原本堆顶的位置。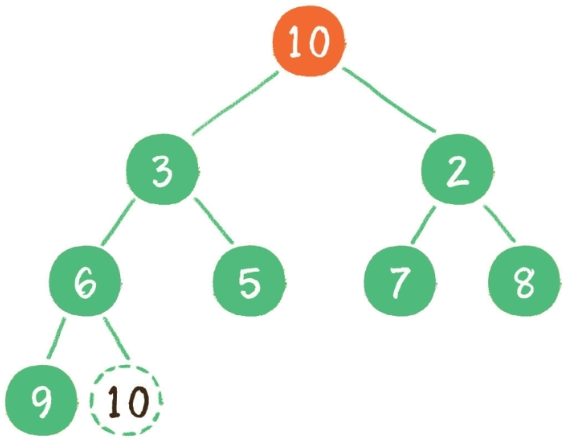
image.png
接下来，让暂处堆顶位置的节点 10 和它的左、右孩子进行比较，如果左、右孩子节点中最小的一个（显然是节点2）比节点 10 小，那么让节点 10“下沉”。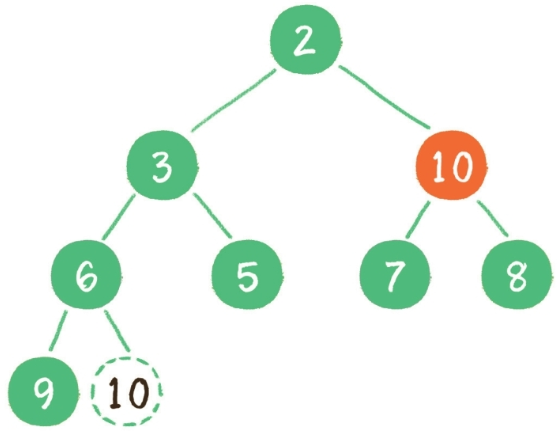
image.png
继续让节点 10 和它的左、右孩子做比较，左、右孩子中最小的是节点 7，由于 10 大于 7，让节点 10 继续“下沉”。
image.png
这样一来，二叉堆重新得到了调整。

3.构建二叉堆

构建二叉堆，也就是把一个无序的完全二叉树调整为二叉堆，本质就是让所有非叶子节点依次“下沉” 。下面举一个无序完全二叉树的例子，如下图所示。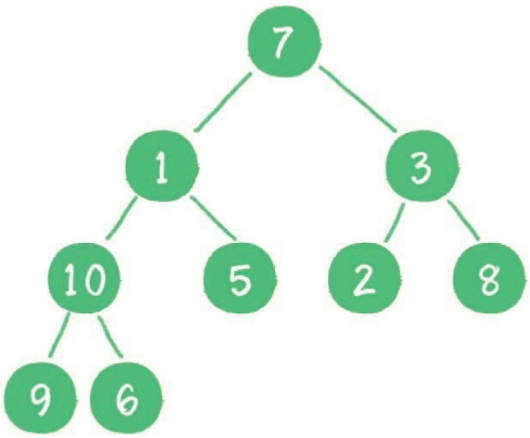
image.png
首先，从最后一个非叶子节点开始，也就是从节点 10 开始。如果节点 10 大于它左、右孩子节点中最小的一个，则节点 10“下沉”。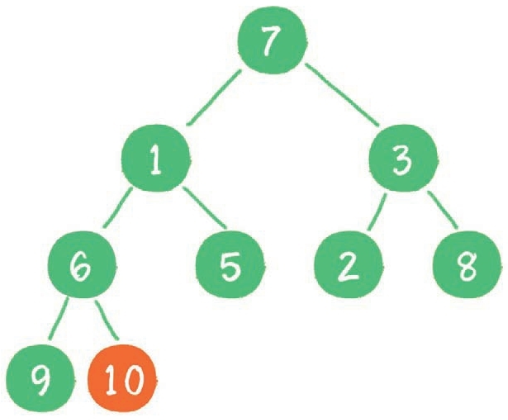
image.png
接下来轮到节点 3，如果节点 3 大于它左、右孩子节点中最小的一个，则节点 3“下沉”。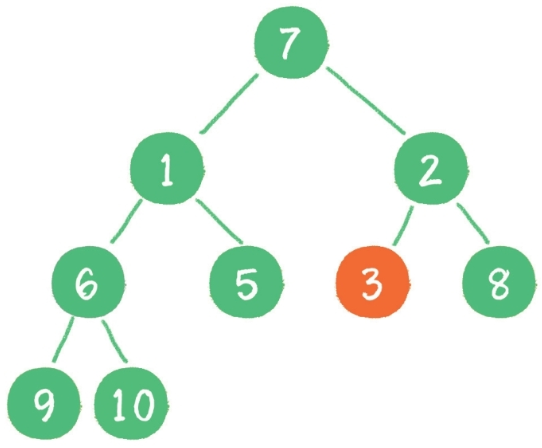
image.png
然后轮到节点 1，如果节点 1 大于它左、右孩子节点中最小的一个，则节点 1“下沉”。事实上节点1小于它的左、右孩子，所以不用改变。接下来轮到节点 7，如果节点 7 大于它左、右孩子节点中最小的一个，则节点 7“下沉”。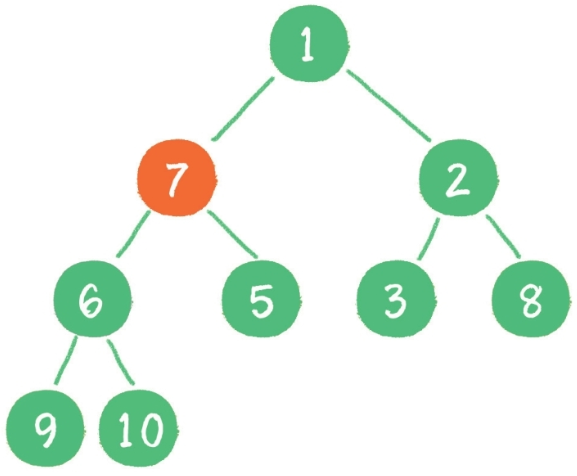
image.png
节点 7 继续比较，继续“下沉”。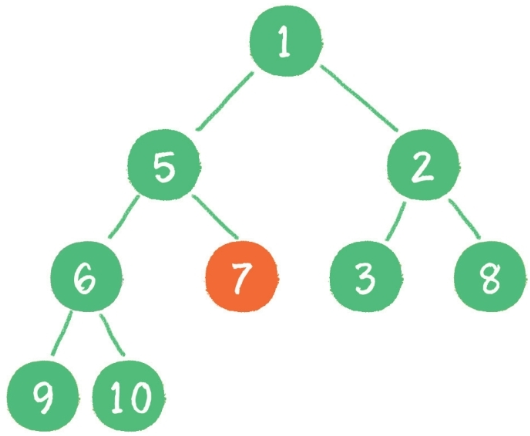
image.png
经过上述几轮比较和“下沉”操作，最终每一节点都小于它的左、右孩子节点，一个无序的完全二叉树就被构建成了一个最小堆。

代码实现

在展示代码之前，我们还需要明确一点：二叉堆虽然是一个完全二叉树，但它的存储方式并不是链式存储，而是顺序存储。换句话说，二叉堆的所有节点都存储在数组中。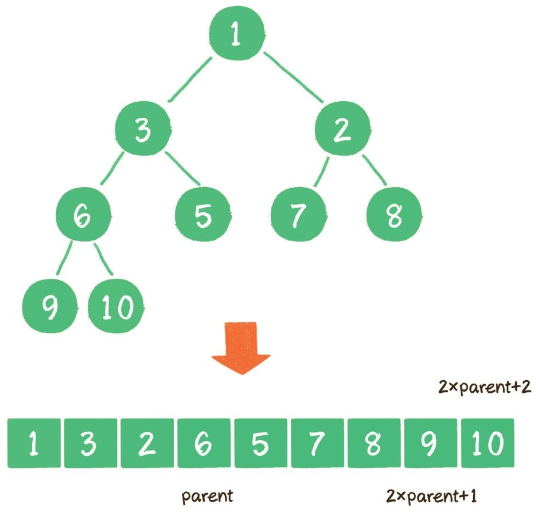
image.png
在数组中，在没有左、右指针的情况下，如何定位一个父节点的左孩子和右孩子呢？
像上图那样，可以依靠数组下标来计算。
假设父节点的下标是 parent，那么它的左孩子下标就是 2 × parent + 1；右孩子下标就是2 × parent + 2。
例如上面的例子中，节点 6 包含 9 和 10 两个孩子节点，节点 6 在数组中的下标是 3，节点 9 在数组中的下标是7，节点 10 在数组中的下标是 8。那么，7=3×2+1，8=3×2+2，刚好符合规律。有了这个前提，下面的代码就更好理解了。

  1. public class BinaryHeap {
  2.     // “上浮”调整
  3.     public static void upAdjust(int[] array) {
  4.         int childIndex = array.length - 1;
  5.         int parentIndex = (childIndex - 1) / 2;
  6.         // temp 保存插入的叶子节点的值，用于最后的赋值
  7.         int temp = array[childIndex];
  8.         while (childIndex > 0 && temp < array[parentIndex]) {
  9.             // 无需真正交换，单项赋值即可
  10.             array[childIndex] = array[parentIndex];
  11.             childIndex = parentIndex;
  12.             parentIndex = (parentIndex - 1) / 2;
  13.         }
  14.         array[childIndex] = temp;
  15.     }
  17.     // “下沉”调整
  18.     public static void downAdjust(int[] array, int parentIndex, int length) {
  19.         // temp 保存父节点值，用于最后的赋值
  20.         int temp = array[parentIndex];
  21.         int childIndex = 2 * parentIndex + 1;
  22.         while (childIndex < length) {
  23.             // 如果有孩子节点，且右孩子节点小于左孩子节点的值，则定位到左孩子
  24.             if (childIndex + 1 < length && array[childIndex + 1] < array[childIndex]) {
  25.                 childIndex++;
  26.             }
  27.             // 如果父节点小于任何一个孩子的值，则直接跳出
  28.             if (temp <= array[childIndex]) break;
  29.             // 无需真正交换，单项赋值即可
  30.             array[parentIndex] = array[childIndex];
  31.             parentIndex = childIndex;
  32.             childIndex = 2 * childIndex + 1;
  33.         }
  34.         array[parentIndex] = temp;
  35.     }
  38.     // 构建堆
  39.     public static void buildHeap(int[] array) {
  40.         // 从最后一个非叶子节点开始，依次做“下沉”操作
  41.         for (int i = (array.length - 1) / 2; i >= 0; i--) {
  42.             downAdjust(array, i, array.length);
  43.         }
  44.     }
  46.     public static void main(String[] args) {
  47.         int[] array = new int[]{1, 3, 2, 6, 5, 7, 8, 9, 10, 0};
  48.         upAdjust(array);
  49.         System.out.println(Arrays.toString(array));
  51.         array = new int[]{7, 1, 3, 10, 5, 2, 8, 9, 6};
  52.         buildHeap(array);
  53.         System.out.println(Arrays.toString(array));
  54.     }
  55. }