构建二叉树

static class TreeNode {
    int data;
    TreeNode leftChild;
    TreeNode rightChild;
    TreeNode(int data) {
        this.data = data;
    }
}

public static TreeNode createBinaryTree(LinkedList<Integer> inputList) {
    TreeNode node = null;
    if (inputList == null || inputList.isEmpty()) {
        return null;
    }
    Integer data = inputList.removeFirst();
    if (data != null) {
        node = new TreeNode(data);
        node.leftChild = createBinaryTree(inputList);
        node.rightChild = createBinaryTree(inputList);
    }
    return node;
}

深度优先(DFS)

1.前序遍历

public static void preOrderTraversal(TreeNode node) {
    if (node == null) {
        return;
    }
    System.out.print(node.data + " ");
    preOrderTraversal(node.leftChild);
    preOrderTraversal(node.rightChild);
}

public static void preOrderTraversalWithStack(TreeNode root) {
    Stack<TreeNode> stack = new Stack<>();
    TreeNode treeNode = root;
    while (treeNode != null || !stack.isEmpty()) {
        // 迭代访问节点左孩子，并入栈
        while (treeNode != null) {
            System.out.println(treeNode.data);
            stack.push(treeNode);
            treeNode = treeNode.leftChild;
        }
        // 如果节点没有左孩子，弹出栈顶节点，访问右孩子
        if (!stack.isEmpty()) {
            treeNode = stack.pop();
            treeNode = treeNode.rightChild;
        }
    }
}

2.中序遍历

public static void inOrderTraversal(TreeNode node) {
    if (node == null) {
        return;
    }
    preOrderTraversal(node.leftChild);
    System.out.print(node.data + " ");
    preOrderTraversal(node.rightChild);
}

3.后续遍历

public static void subSequentTraversal(TreeNode node) {
    if (node == null) {
        return;
    }
    preOrderTraversal(node.leftChild);
    preOrderTraversal(node.rightChild);
    System.out.print(node.data + " ");
}

public static void main(String[] args) {
    LinkedList<Integer> inputList = new LinkedList<>(Arrays.asList(3, 2, 9, null, null, 10, null,
                                                                   null, 8, null, 4));
    TreeNode treeNode = createBinaryTree(inputList);
    preOrderTraversal(treeNode);
    System.out.println();
    inOrderTraversal(treeNode);
    System.out.println();
    subSequentTraversal(treeNode);
}
/** output
 * 3 2 9 10 8 4 
 * 2 9 10 3 8 4 
 * 2 9 10 8 4 3 
 */

广度优先(BFS)

详细遍历步骤如下。

根节点 1 进入队列。

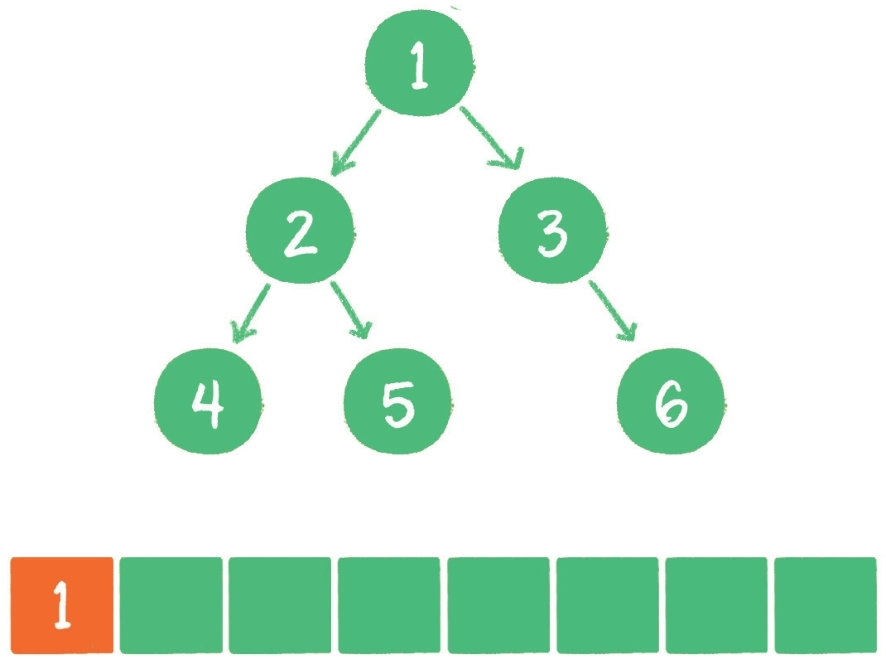
节点 1 出队，输出节点 1，并得到节点 1 的左孩子节点 2、右孩子节点 3。让节点 2 和节点 3 入队。

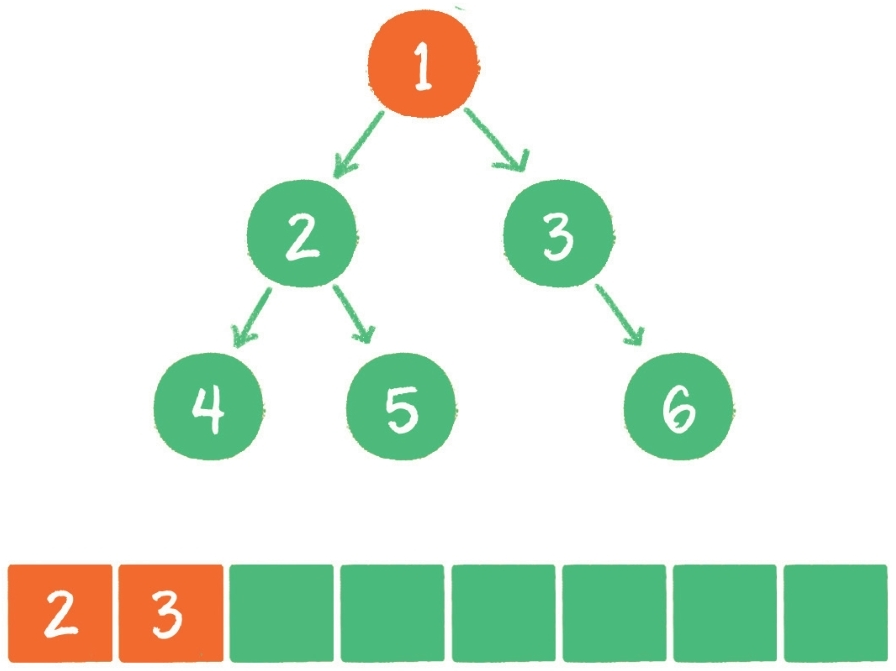
节点 2 出队，输出节点 2，并得到节点 2 的左孩子节点 4、右孩子节点 5。让节点 4 和节点 5 入队。

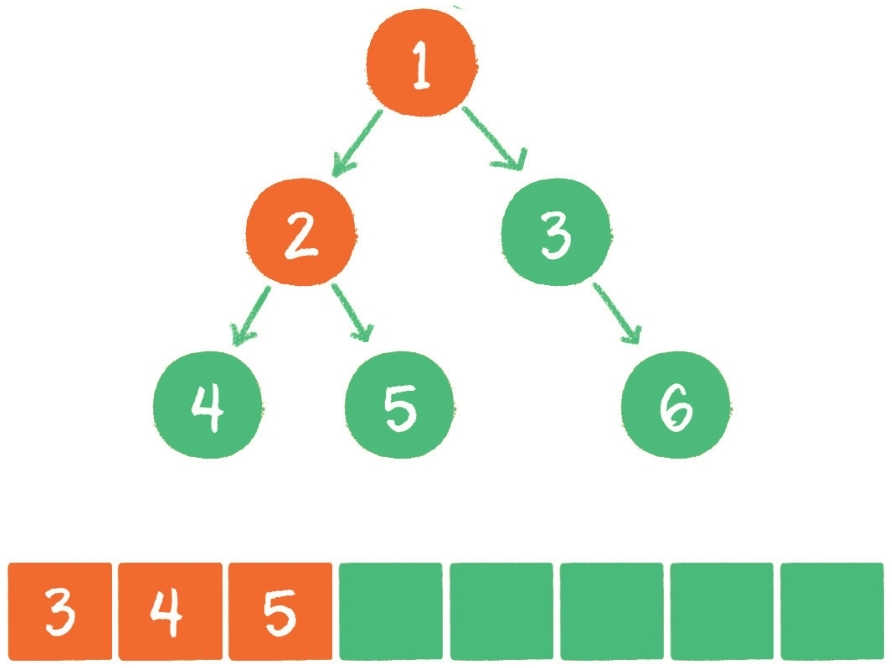
节点 3 出队，输出节点 3，并得到节点 3 的右孩子节点 6。让节点 6 入队。

节点 4 出队，输出节点 4，由于节点 4 没有孩子节点，所以没有新节点入队。

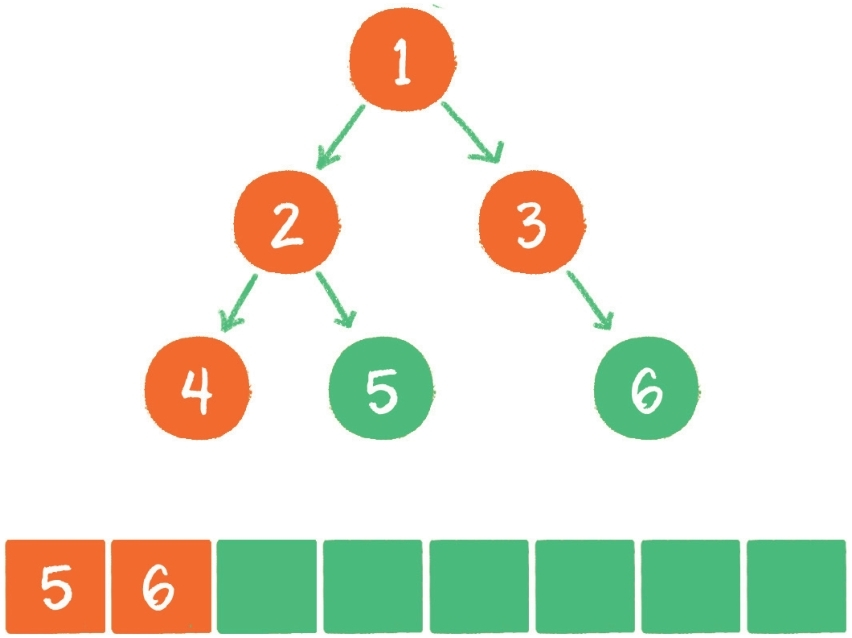
节点 5 出队，输出节点 5，由于节点 5 同样没有孩子节点，所以没有新节点入队。

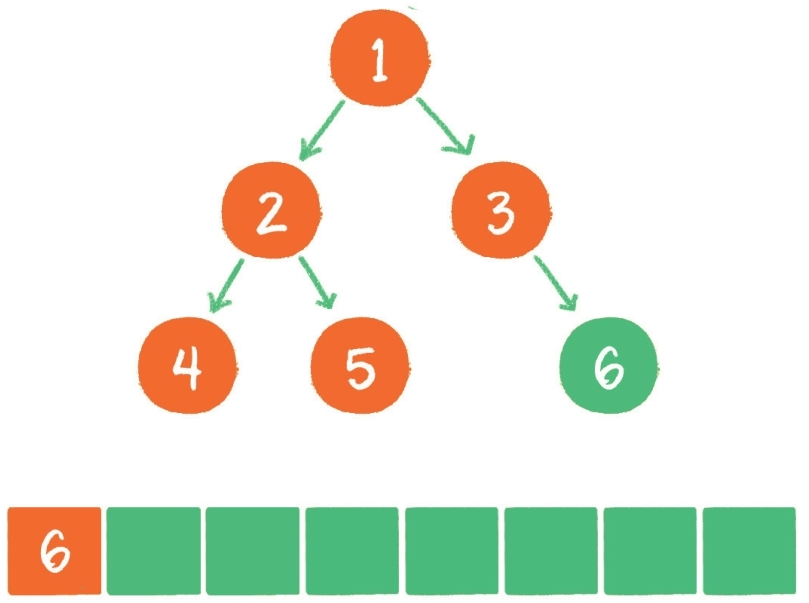
节点 6 出队，输出节点 6，节点 6 没有孩子节点，没有新节点入队。

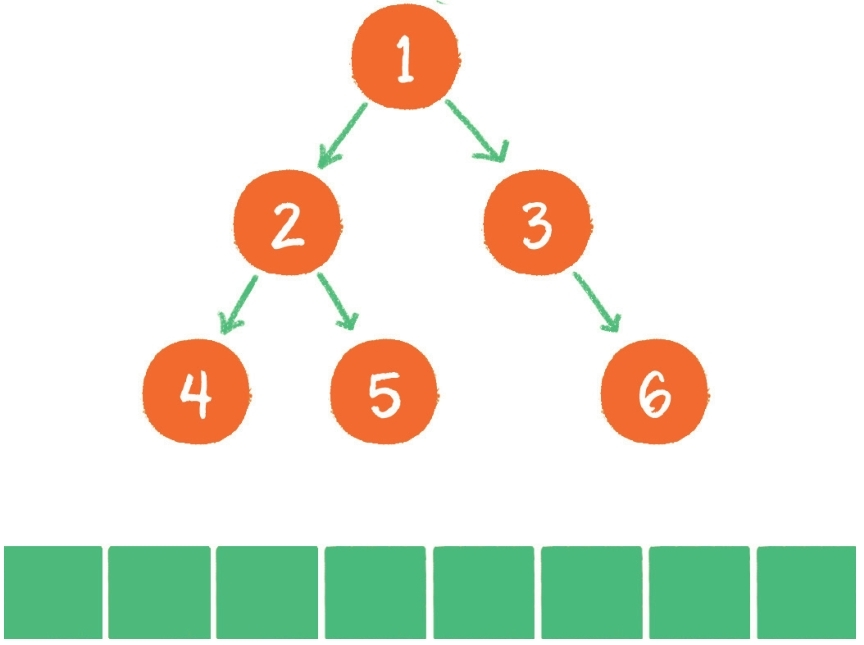
到此为止，所有的节点都遍历输出完毕。

public static void levelOrderTraversal(TreeNode root) {
    Queue<TreeNode> queue = new LinkedList<>();
    queue.offer(root);
    while (!queue.isEmpty()) {
        TreeNode node = queue.poll();
        System.out.println(node.data);
        if (node.leftChild != null) {
            queue.offer(node.leftChild);
        }
        if (node.rightChild != null) {
            queue.offer(node.rightChild);
        }
    }
}

二叉搜索树

有效二叉搜索树定义如下：

节点的左子树只包含小于当前节点的数。
节点的右子树只包含大于当前节点的数。
所有左子树和右子树自身必须也是二叉搜索树。
思路

二叉树的中序遍历

根据二叉树搜索树的特点可知，二叉搜索树的中序遍历一定是有序的。

public boolean isValidBST(TreeNode root) {
    Deque<TreeNode> stack = new LinkedList<>();
    double inorder = -Double.MAX_VALUE;
    while (!stack.isEmpty() || root != null) {
        while (root != null) {
            stack.push(root);
            root = root.left;
        }
        root = stack.pop();
        // 如果中序遍历得到的节点的值小于等于前一个 inorder，说明不是二叉搜索树
        if (root.val <= inorder) {
            return false;
        }
        inorder = root.val;
        root = root.right;
    }
    return true;
}

递归

递归时判断每个子节点是否在给定范围内

public boolean isValidBST(TreeNode root) {
    return isValidBST(root, Long.MIN_VALUE, Long.MAX_VALUE);
}

public boolean isValidBST(TreeNode root, long min, long max) {
    if (root == null) return true;
    if (root.val <= min || root.val >= max) return false;
    return isValidBST(root.left, min, root.val) && isValidBST(root.right, root.val, max);
}

对称二叉树

给你一个二叉树的根节点 root ，检查它是否轴对称。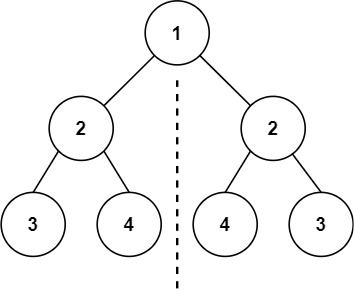

输入：root = [1,2,2,3,4,4,3]
输出：true

public boolean isSymmetric(TreeNode root) {
    if (root == null) return true;
    return isSymmetric(root.left, root.right);
}

public boolean isSymmetric(TreeNode left, TreeNode right) {
    if (left == null && right == null) return true;
    if (left == null || right == null || left.val != right.val) return false;
    return isSymmetric(left.left, right.right) && isSymmetric(left.right, right.left);
}

public boolean isSymmetric2(TreeNode root) {
    // 队列
    Queue<TreeNode> queue = new LinkedList<>();
    if (root == null) return true;
    // 左子节点和右子节点同时入队
    queue.add(root.left);
    queue.add(root.right);
    // 如果队列不为空就继续循环
    while (!queue.isEmpty()) {
        // 每两个出队
        TreeNode left = queue.poll(), right = queue.poll();
        // 如果都为空继续循环
        if (left == null && right == null)
            continue;
        // 如果一个为空一个不为空，说明不是对称的，直接返回false
        if (left == null ^ right == null)
            return false;
        // 如果这两个值不相同，也不是对称的，直接返回false
        if (left.val != right.val)
            return false;
        // 这里要记住入队的顺序，他会每两个两个的出队。
        // 左子节点的左子节点和右子节点的右子节点同时
        // 入队，因为他俩会同时比较。
        // 左子节点的右子节点和右子节点的左子节点同时入队，
        // 因为他俩会同时比较
        queue.add(left.left);
        queue.add(right.right);
        queue.add(left.right);
        queue.add(right.left);
    }
    return true;
}

二叉树

构建二叉树

深度优先(DFS)

1.前序遍历

2.中序遍历

3.后续遍历

广度优先(BFS)

二叉搜索树

思路

对称二叉树