笔记 - A* 寻路算法 - 《算法》

用一个简单的场景来举例，咱们看一看A星寻路算法的工作过程。

迷宫游戏的场景通常都是由小方格组成的。假设我们有一个7×5大小的迷宫，上图中绿色的格子是起点，红色的格子是终点，中间的3个蓝色格子是一堵墙。
AI角色从起点开始，每一步只能向上下/左右移动1格，且不能穿越墙壁。那么如何让AI角色用最少的步数到达终点呢？
在解决这个问题之前，我们先引入2个集合和1个公式。
两个集合如下。

OpenList：可到达的格子
CloseList：已到达的格子

一个公式如下。

每一个格子都具有F、G、H这3个属性，就像下图这样。

G：从起点走到当前格子的成本，也就是已经花费了多少步。
H：在不考虑障碍的情况下，从当前格子走到目标格子的距离，也就是离目标还有多远。
F：G和H的综合评估，也就是从起点到达当前格子，再从当前格子到达目标格子的总步数。
我们通过实际场景来分析一下，你就明白了。
第1步，把起点放入OpenList，也就是刚才所说的可到达格子的集合。

第2步，找出OpenList中F值最小的方格作为当前方格。虽然我们没有直接计算起点方格的F值，但此时OpenList中只有唯一的方格Grid（1，2），把当前格子移出OpenList，放入CloseList。代表这个格子已到达并检查过了。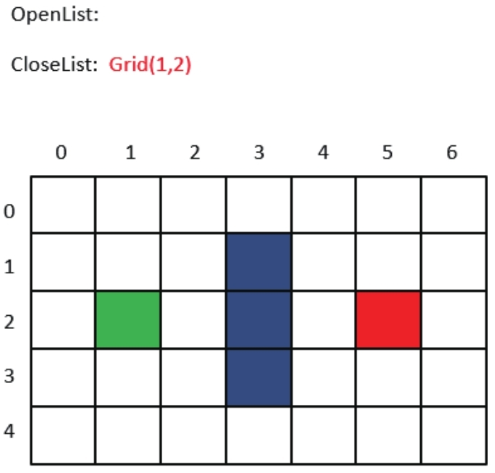

第3步，找出当前方格（刚刚检查过的格子）上、下、左、右所有可到达的格子，看它们是否在OpenList或CloseList当中。如果不在，则将它们加入OpenList，计算出相应的G、H、F值，并把当前格子作为它们的“父节点”。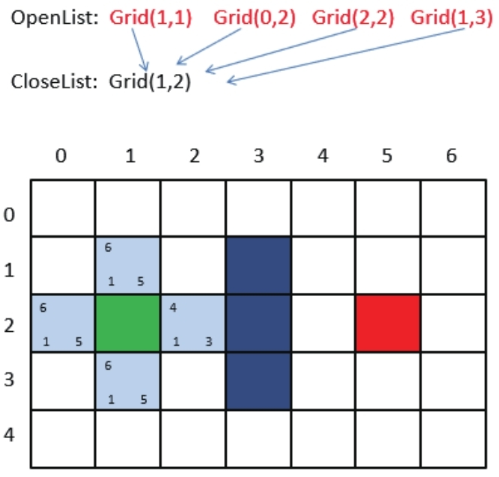

在上图中，每个格子的左下方数字是G，右下方是H，左上方是F。
一个格子的“父节点”代表它的来路，在输出最终路线时会用到。
刚才经历的几个步骤是一次局部寻路的步骤。我们需要一次又一次重复刚才的第2步和第3步，直到找到终点为止。
下面进入A星寻路的第2轮操作。
第1步，找出OpenList中F值最小的方格，即方格Grid（2，2），将它作为当前方格，并把当前方格移出OpenList，放入CloseList。代表这个格子已到达并检查过了。

第2步，找出当前方格上、下、左、右所有可到达的格子，看它们是否在OpenList或CloseList当中。如果不在，则将它们加入OpenList，计算出相应的G、H、F值，并把当前格子作为它们的“父节点”。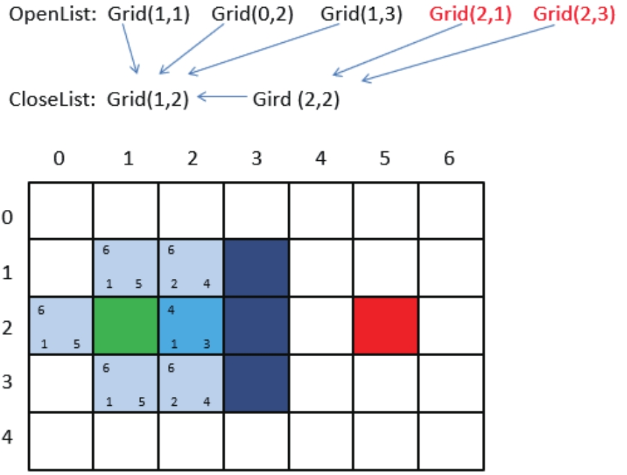

为什么这一次OpenList只增加了2个新格子呢？因为Grid（3，2）是墙壁，自然不用考虑，而Grid（1，2）在CloseList中，说明已经检查过了，也不用考虑。
下面我们进入第3轮寻路历程。
第1步，找出OpenList中F值最小的方格。由于此时有多个方格的F值相等，任意选择一个即可，如将Grid（2，3）作为当前方格，并把当前方格移出OpenList，放入CloseList。代表这个格子已到达并检查过了。

第2步，找出当前方格上、下、左、右所有可到达的格子，看它们是否在OpenList当中。如果不在，则将它们加入OpenList，计算出相应的G、H、F值，并把当前格子作为它们的“父节点”。

剩下的就是以前面的方式继续迭代，直到OpenList中出现终点方格为止。这里我们仅仅使用图片简单描述一下，方格中的数字表示F值。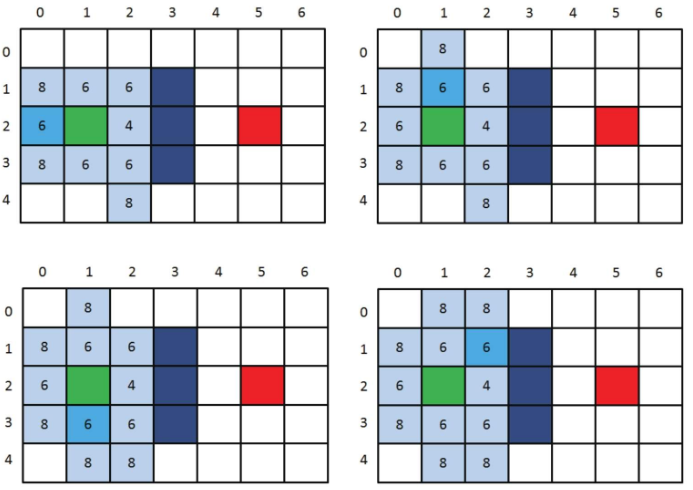

像这样一步一步来，当终点出现在OpenList中时，我们的寻路之旅就结束了。
还记得刚才方格之间的父子关系吗？我们只要顺着终点方格找到它的父亲，再找到父亲的父亲……如此依次回溯，就能找到一条最佳路径了。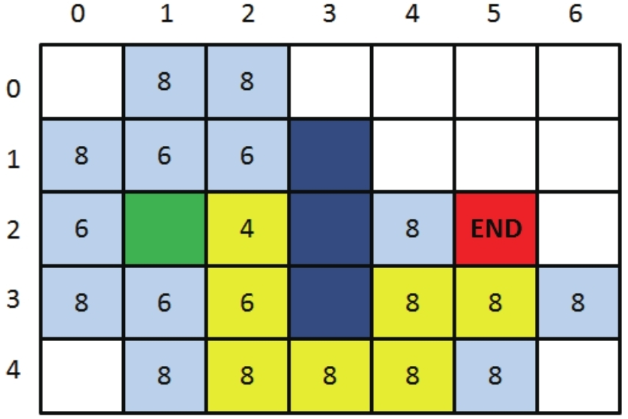

这就是A星寻路算法的基本思想。像这样以估值高低来决定搜索优先次序的方法，被称为启发式搜索。

class Grid {
    public int x;
    public int y;
    public int f;
    public int g;
    public int h;
    public Grid parent;
    public Grid(int x, int y) {
        this.x = x;
        this.y = y;
    }
    public void initGrid(Grid parent, Grid end) {
        this.parent = parent;
        if (parent != null) {
            this.g = parent.g + 1;
        } else {
            this.g = 1;
        }
        this.h = Math.abs(this.x - end.x) + Math.abs(this.y - end.y);
        this.f = this.g + this.h;
    }
}
public class AStarSearch {
    // 迷宫地图
    public static final int[][] MAZE = {
            {0, 0, 0, 0, 0, 0, 0},
            {0, 0, 0, 1, 0, 0, 0},
            {0, 0, 0, 1, 0, 0, 0},
            {0, 0, 0, 1, 0, 0, 0},
            {0, 0, 0, 0, 0, 0, 0}
    };
    private static boolean containGrid(List<Grid> grids, int x, int y) {
        for (Grid n : grids) {
            if ((n.x == x) && (n.y == y)) {
                return true;
            }
        }
        return false;
    }
    private static boolean isValidGrid(int x, int y, List<Grid> openList, List<Grid> closeList) {
        // 是否超过边界
        if (x < 0 || x >= MAZE.length || y < 0 || y >= MAZE[0].length) return false;
        // 是否有障碍物
        if (MAZE[x][y] == 1) return false;
        // 是否已经在 openList 中
        if (containGrid(openList, x, y)) return false;
        // 是否已经在 closeList 中
        if (containGrid(closeList, x, y)) return false;
        return true;
    }
    private static ArrayList<Grid> findNeighbors(Grid grid, List<Grid> openList, List<Grid> closeList) {
        ArrayList<Grid> gridList = new ArrayList<>();
        if (isValidGrid(grid.x, grid.y - 1, openList, closeList)) {
            gridList.add(new Grid(grid.x, grid.y - 1));
        }
        if (isValidGrid(grid.x, grid.y + 1, openList, closeList)) {
            gridList.add(new Grid(grid.x, grid.y + 1));
        }
        if (isValidGrid(grid.x - 1, grid.y, openList, closeList)) {
            gridList.add(new Grid(grid.x - 1, grid.y));
        }
        if (isValidGrid(grid.x + 1, grid.y, openList, closeList)) {
            gridList.add(new Grid(grid.x + 1, grid.y));
        }
        return gridList;
    }
    private static Grid findMinGird(ArrayList<Grid> openList) {
        Grid tempGrid = openList.get(0);
        for (Grid grid : openList) {
            if (grid.f < tempGrid.f) {
                tempGrid = grid;
            }
        }
        return tempGrid;
    }
    // 主逻辑
    public static Grid aStartSearch(Grid start, Grid end) {
        ArrayList<Grid> openList = new ArrayList<>();
        ArrayList<Grid> closeList = new ArrayList<>();
        // 把起点加入 openList
        openList.add(start);
        // 主循环，每一轮检测一个当前方格节点
        while (openList.size() > 0) {
            // 在 openList 中查找 F 值最小的节点，将其作为当前方格节点
            Grid currentGrid = findMinGird(openList);
            // 将当前节点从 openList 中删除
            openList.remove(currentGrid);
            // 当前方格节点进入 closeList
            closeList.add(currentGrid);
            // 找到所有邻近节点
            ArrayList<Grid> neighbors = findNeighbors(currentGrid, openList, closeList);
            for (Grid grid : neighbors) {
                if (!openList.contains(grid)) {
                    // 邻近节点不在 openList 中，标记“父节点”、G、H、F，并放入 openList
                    grid.initGrid(currentGrid, end);
                    openList.add(grid);
                }
            }
            // 如果终点在 openList 中，直接返回终点格子
            for (Grid grid : openList) {
                if ((grid.x == end.x) && (grid.y == end.y)) {
                    return grid;
                }
            }
        }
        // openList 用尽，仍然找不到终点，说明终点不可到达，返回空
        return null;
    }
    public static void main(String[] args) {
        // 设置起点和终点
        Grid start = new Grid(2, 1);
        Grid end = new Grid(2, 5);
        // 搜索迷宫终点
        Grid resultGrid = aStartSearch(start, end);
        // 回溯迷宫路径
        ArrayList<Grid> path = new ArrayList<>();
        while (resultGrid != null) {
            path.add(new Grid(resultGrid.x, resultGrid.y));
            resultGrid = resultGrid.parent;
        }
        // 输出迷宫和路径，路径用 * 表示
        for (int i = 0; i < MAZE.length; i++) {
            for (int j = 0; j < MAZE[0].length; j++) {
                if (containGrid(path, i, j)) {
                    System.out.print("*, ");
                } else {
                    System.out.print(MAZE[i][j] + ", ");
                }
            }
            System.out.println();
        }
    }
}