很久很久以前，有一位国王拥有5座金矿，每座金矿的黄金储量不同，需要参与挖掘的工人人数也不同。例如有的金矿储量是500kg黄金，需要5个工人来挖掘；有的金矿储量是200kg黄金，需要3个工人来挖掘……
如果参与挖矿的工人的总数是10。每座金矿要么全挖，要么不挖，不能派出一半人挖取一半的金矿。要求用程序求出，要想得到尽可能多的黄金，应该选择挖取哪几座金矿？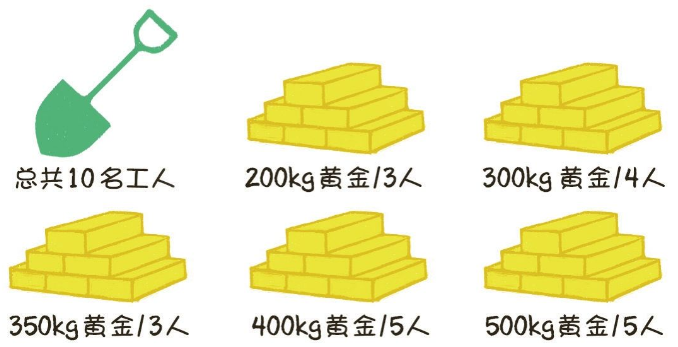
image.png

首先，对于问题中的金矿来说，每一个金矿都存在着“挖”和“不挖”两种选择。让我们假设一下，如果最后一个金矿注定不被挖掘，那么问题会转化成什么样子呢？显然，问题简化成了10个工人在前4个金矿中做出最优选择。
相应地，假设最后一个金矿一定会被挖掘，那么问题又转化成什么样子呢？由于最后一个金矿消耗了3个工人，问题简化成了7个工人在前4个金矿中做出最优选择。
这两种简化情况，被称为全局问题的两个最优子结构。
究竟哪一种最优子结构可以通向全局最优解呢？换句话说，最后一个金矿到底该不该挖呢？
那就要看10个工人在前4个金矿的收益，和7个工人在前4个金矿的收益+最后一个金矿的收益谁大谁小了。
同样的道理，对于前4个金矿的选择，我们还可以做进一步简化。
首先针对10个工人4个金矿这个子结构，第4个金矿（300kg黄金/4人）可以选择挖与不挖。根据第4个金矿的选择，问题又简化成了两种更小的子结构。

  1. 10个工人在前3个金矿中做出最优选择。
  2. 6（10-4=6）个工人在前3个金矿中做出最优选择。

相应地，对于7个工人4个金矿这个子结构，第4个金矿同样可以选择挖与不挖。根据第4个金矿的选择，问题也简化成了两种更小的子结构。

  1. 7个工人在前3个金矿中做出最优选择。
  2. 3（7-4=3）个工人在前3个金矿中做出最优选择。

……
就这样，问题一分为二，二分为四，一直把问题简化成在0个金矿或0个工人时的最优选择，这个收益结果显然是0，也就是问题的边界。
这就是动态规划的要点：确定全局最优解和最优子结构之间的关系，以及问题的边界。
这个关系用数学公式来表达的话，就叫作状态转移方程式。
我们把金矿数量设为 n，工人数量设为 w，金矿的含金量设为数组 g[]，金矿所需开采人数设为数组 p[]，设 F(n，w) 为 n 个金矿、w 个工人时的最优收益函数，那么状态转移方程式如下。
动态规划 - 图2
问题边界，金矿数为0或工人数为0的情况。
动态规划 - 图3
当所剩工人不够挖掘当前金矿时，只有一种最优子结构。
动态规划 - 图4
在常规情况下，具有两种最优子结构（挖当前金矿或不挖当前金矿）。
在进行求解之前，先准备一张表格，用于记录选择金矿的中间数据。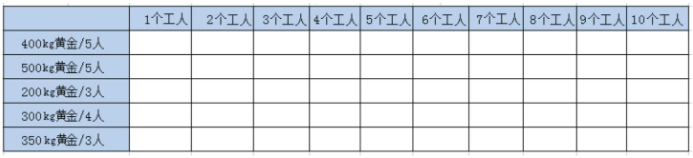
image.png
表格最左侧代表不同的金矿选择范围，从上到下，每多增加1行，就代表多1个金矿可供选择，也就是 F(n, w) 函数中的 n 值。
表格的最上方代表工人数量，从1个工人到10个工人，也就是 F(n, w) 函数中的 w 值。
其余空白的格子，都是等待填写的，代表当给出 n 个金矿、w 个工人时的最优收益，也就是 F(n, w) 的值。
下面让我们从第1行第1列开始，尝试把空白的格子一一填满，填充的依据就是状态转移方程式。
对于第1行的前4个格子，由于w＜p[n -1]，对应的状态转移方程式如下：
动态规划 - 图6
带入求解：
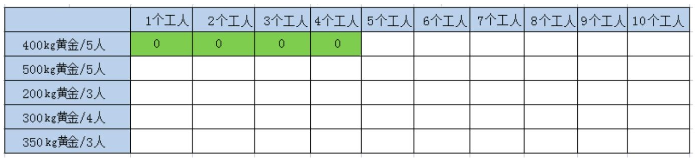
image.png
第1行的后6个格子怎么计算呢？此时w ≥p[n -1]，对于如下公式：
动态规划 - 图8
带入求解：
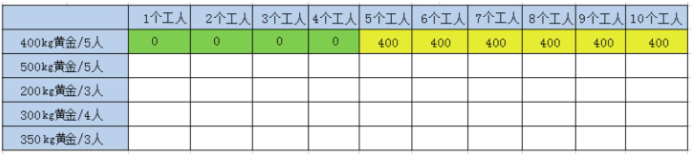
image.png
……
最终我们会得到如下结果：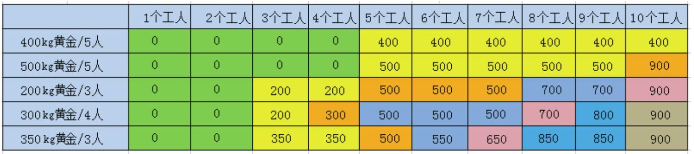
image.png

  1. /**
  2.  * @param w 人数
  3.  * @param p 每个矿需要的人数
  4.  * @param g 矿的价值
  5.  * @return 收益
  6.  */
  7. public static int getBestGoldMining(int w, int[] p, int[] g) {
  8.     // 创建表格
  9.     int[][] resultTable = new int[g.length + 1][w + 1];
  10.     // 填充表格
  11.     for (int i = 1; i <= g.length; i++) {
  12.         for (int j = 1; j <= w; j++) {
  13.             if (j < p[i - 1]) {
  14.                 resultTable[i][j] = resultTable[i - 1][j];
  15.             } else {
  16.                 resultTable[i][j] = Math.max(resultTable[i - 1][j], resultTable[i - 1][j - p[i - 1]] + g[i - 1]);
  17.             }
  18.         }
  19.     }
  20.     // 返回最后一个格子的值
  21.     return resultTable[g.length][w];
  22. }

时间复杂度和空间复杂度都是动态规划 - 图11。

优化

在表格中除第1行之外，每一行的结果都是由上一行数据 推导出来的。我们以4个金矿9个工人为例。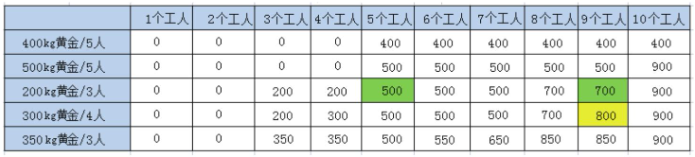
image.png
4个金矿、9个工人的最优结果，是由它的两个最优子结构，也就是3个金矿、5个工人和3个金矿、9个工人的结果推导而来的。这两个最优子结构都位于它的上一行。
所以，在程序中并不需要保存整个表格，无论金矿有多少座，我们只保存1行的数据即可。在计算下一行时，要从右向左统计（读者可以想想为什么从右向左），把旧的数据一个一个替换掉。

/**
 * @param w 人数
 * @param p 每个矿需要的人数
 * @param g 矿的价值
 * @return 收益
 */
public static int getBestGoldMining2(int w, int[] p, int[] g) {
    // 创建当前结果
    int[] results = new int[w + 1];
    // 填充一维数组
    for (int i = 1; i <= g.length; i++) {
        for (int j = w; j >= 1; j--) {
            if (j >= p[i - 1]) {
                results[j] = Math.max(results[j], results[j - p[i - 1]] + g[i - 1]);
            }
        }
    }
    // 返回最后一个格子的值
    return results[w];
}

空间复杂度动态规划 - 图13。