详解

KMP 算法是一种改进的字符串匹配算法,其关键是利用匹配失败后的信息,尽量减少模式串与主串的匹配次数以达到快速匹配的目的。
KMP 算法的核心，是一个被称为匹配表（Partial Match Table）的数组。
以字符串 “abababca” 为例，它的 PMT 如下表所示：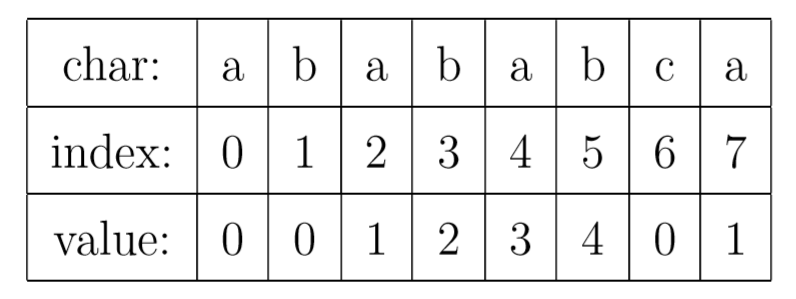
v2-e905ece7e7d8be90afc62fe9595a9b0f_r.png
其中 index 表示每个字符的索引值，value 为其对应的 PMT 值。
对于 value 是如何获取的，我们首先需要了解两个概念「前缀」和「后缀」。我们通过举例说明：对于字符 “Harry”，它的前缀包括 {“H”, “Ha”, “Har”, “Harr”}，它的后缀包括 {“array”, “rry”, “ry”, “y”}。这里需要说明的是，字符串本身并不是它的前缀或后缀。 :::info 现在我们来看看 value 中的值是如何产生的。 ::: value 中的值实际上就是子串[0, index]的前缀集合和后缀集合的交集中的最长元素的长度。 :::tips 举例：
对于字符 “a”，前缀集合为 {“”}，后缀集合为 {“”}，交集为 {“”}，最长子串为 “”，value=0；
对于字符 “ab”，前缀集合为 {“a”}，后缀集合为 {“b”}，交集为 {“”}，最长子串为 “”，value=0；
对于字符 “aba”，前缀集合为 {“a”, “ab”}，后缀集合为 {“a”, “ba”}，交集为 {“a”}，最长子串为 “a”，value=1；
对于字符 “abab”，前缀集合为 {“a”, “ab”, “aba”}，后缀集合为 {“b”, “ab”, “bab”}，交集为 {“ab”}，最长子串为 “ab”，value=2；
对于字符 “ababa”，前缀集合为 {“a”, “ab”, “aba”, “abab”}，后缀集合为 {“a”, “ba”, “aba”, “baba”}，交集为 {“a”, “aba”}，最长子串为 “aba”，value=3；
… ::: 好了，解释清楚这个表是什么之后，我们再来看如何使用这个表来加速字符串的查找，以及这样用的道理是什么。如图 1.12 所示，要在主字符串 “ababababca” 中查找模式字符串 “abababca”。如果在 j 处字符不匹配，那么由于前边所说的模式字符串 PMT 的性质，主字符串中 i 指针之前的 PMT[j −1] 位就一定与模式字符串的第 0 位至第 PMT[j−1] 位是相同的。这是因为主字符串在 i 位失配，也就意味着主字符串从 i−j 到 i 这一段是与模式字符串的 0 到 j 这一段是完全相同的。而我们上面也解释了，模式字符串从 0 到 j−1 ，在这个例子中就是 “ababab”，其前缀集合与后缀集合的交集的最长元素为 “abab”， 长度为 4。所以就可以断言，主字符串中 i 指针之前的 4 位一定与模式字符串的第 0 位至第 4 位是相同的，即长度为 4 的后缀与前缀相同。这样一来，我们就可以将这些字符段的比较省略掉。具体的做法是，保持 i 指针不动，然后将 j 指针指向模式字符串的 PMT[j −1] 位即可。
简言之，以图中的例子来说，在 i 处失配，那么主字符串和模式字符串的前边6位就是相同的。又因为模式字符串的前6位，它的前4位前缀和后4位后缀是相同的，所以我们推知主字符串i之前的4位和模式字符串开头的4位是相同的。就是图中的灰色部分。那这部分就不用再比较了。
v2-03a0d005badd0b8e7116d8d07947681c_r.jpg
有了上面的思路，我们就可以使用 PMT 加速字符串的查找了。我们看到如果是在 j 位失配，那么影响 j 指针回溯的位置的其实是第 j −1 位的 PMT 值，所以为了编程的方便， 我们不直接使用 PMT 数组，而是将 PMT 数组向后偏移一位。我们把新得到的这个数组称为 next 数组。下面给出根据 next 数组进行字符串匹配加速的字符串匹配程序。其中要注意的一个技巧是，在把 PMT 进行向右偏移时，第 0 位的值，我们将其设成了 -1，这只是为了编程的方便，并没有其他的意义。在本节的例子中，next 数组如下表所示: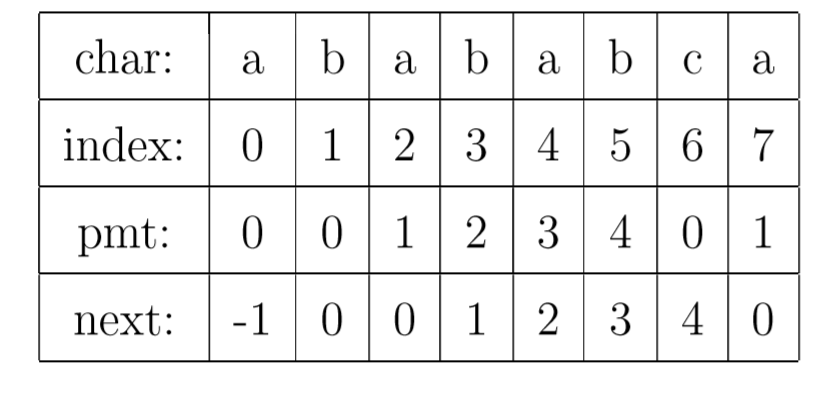
v2-40b4885aace7b31499da9b90b7c46ed3_r.png
具体的程序如下所示：s

  1. int KMP(char * t, char * p) 
  2. {
  3.     int i = 0; 
  4.     int j = 0;
  6.     while (i < (int)strlen(t) && j < (int)strlen(p))
  7.     {
  8.         if (j == -1 || t[i] == p[j]) 
  9.         {
  10.             i++;
  11.             j++;
  12.         }
  13.         else 
  14.             j = next[j];
  15.     }
  17.     if (j == strlen(p))
  18.         return i - j;
  19.     else 
  20.         return -1;
  21. }

现在，我们再看一下如何编程快速求得 next 数组。其实，求 next 数组的过程完全可以看成字符串匹配的过程，即以模式字符串为主字符串，以模式字符串的前缀为目标字符串，一旦字符串匹配成功，那么当前的 next 值就是匹配成功的字符串的长度。
具体来说，就是从模式字符串的第一位(注意，不包括第 0 位)开始对自身进行匹配运算。在任一位置，能匹配的最长长度就是当前位置的 next 值。如下图所示。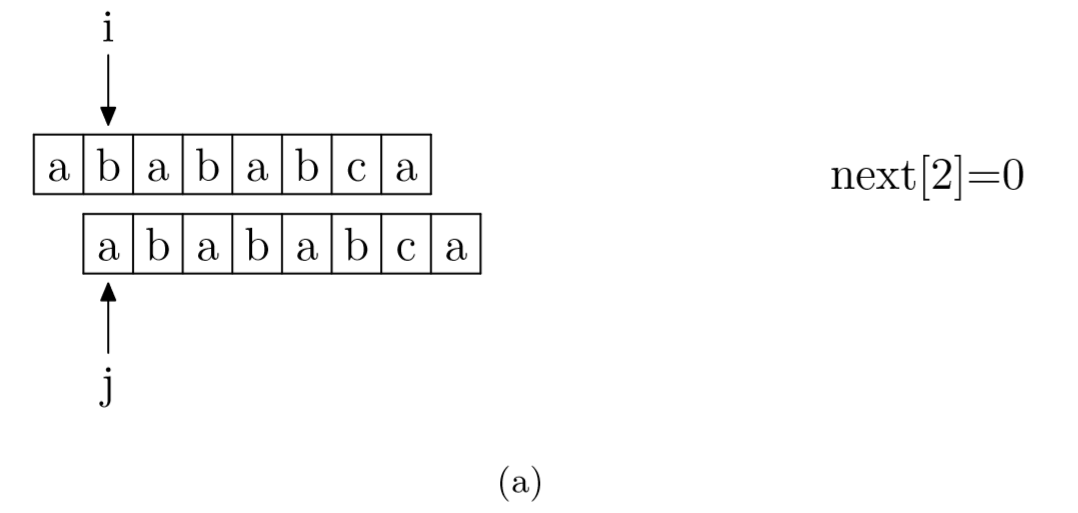
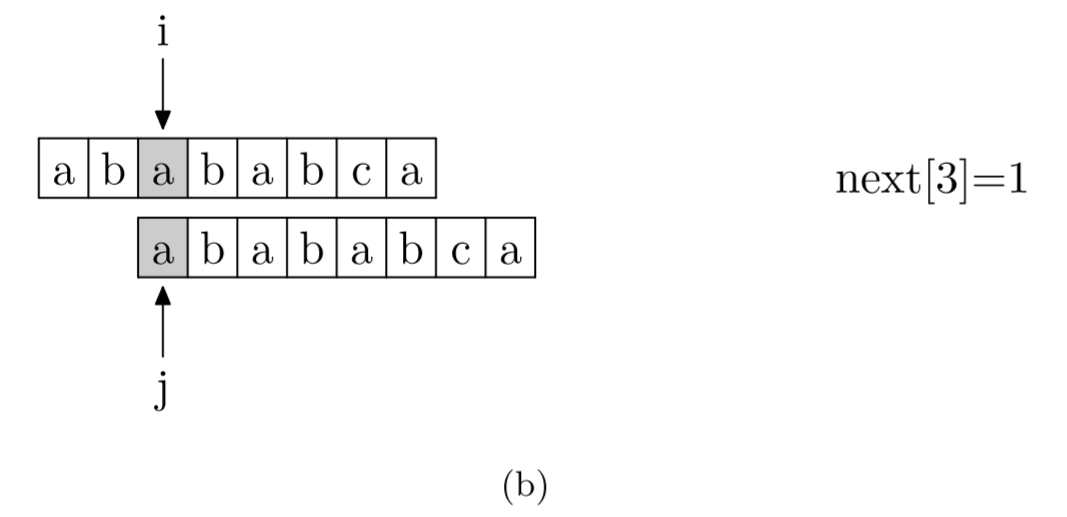
v2-645f3ec49836d3c680869403e74f7934_r.png v2-06477b79eadce2d7d22b4410b0d49aba_r.png
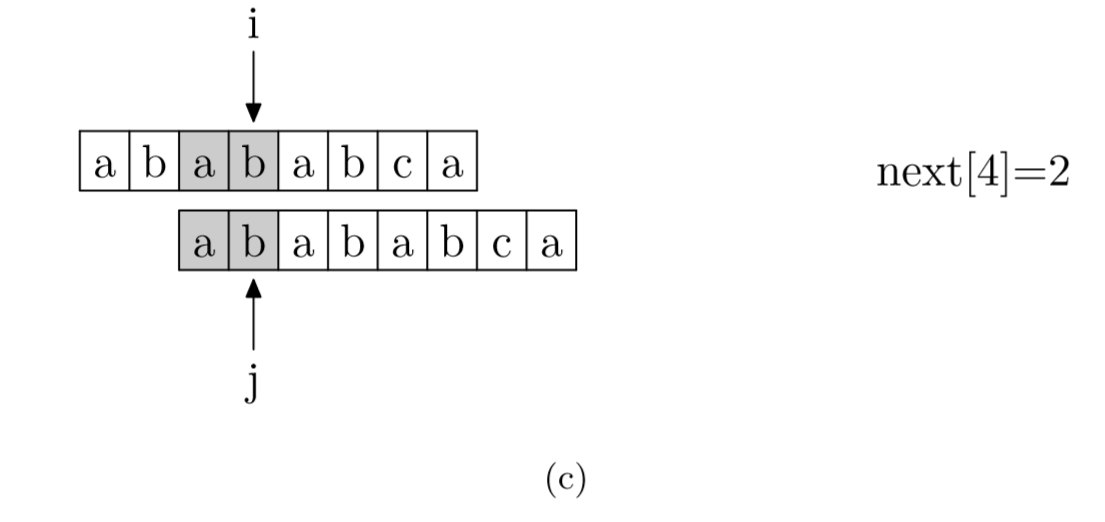
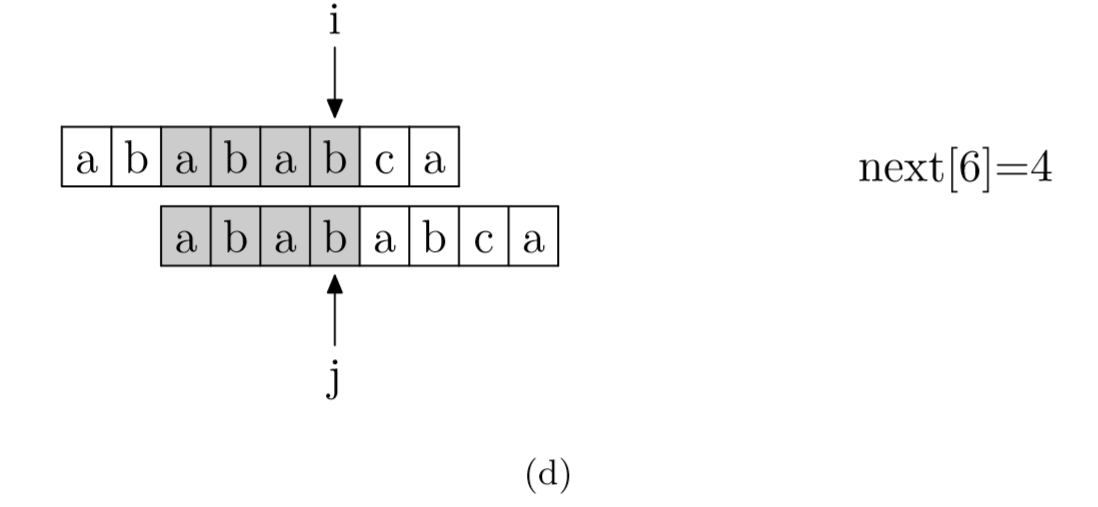
v2-8a1a205df5cad7ab2f07498484a54a89_r.png v2-f2b50c15e7744a7b358154610204cc62_r.png
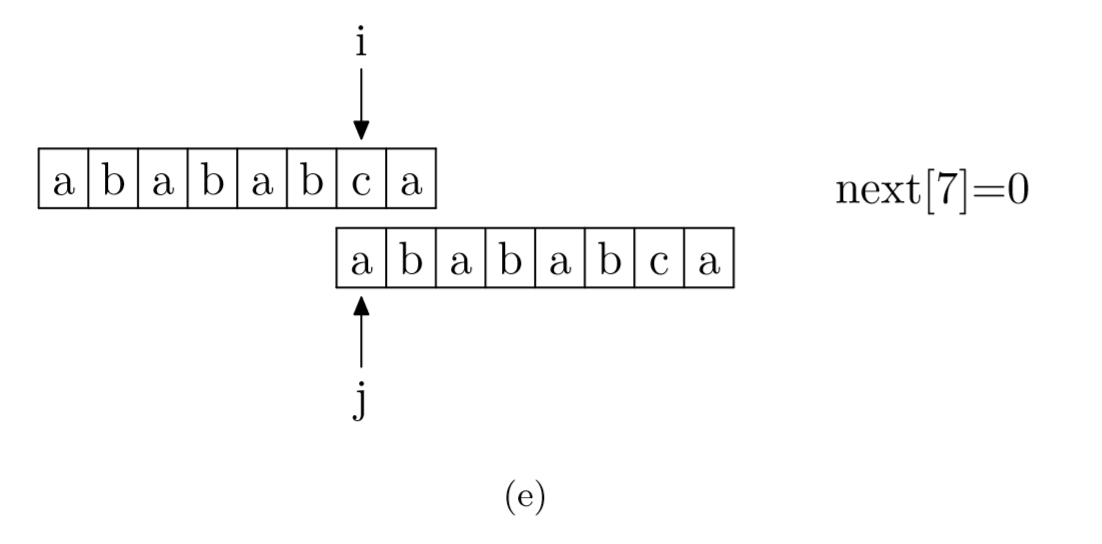
v2-bd42e34a9266717b63706087a81092ac_r.png
求 next 数组值的程序如下所示：

void getNext(char * p, int * next)
{
    next[0] = -1;
    int i = 0, j = -1;

    while (i < (int)strlen(p))
    {
        if (j == -1 || p[i] == p[j])
        {
            ++i;
            ++j;
            next[i] = j;
        }    
        else
            j = next[j];
    }
}

例题

:::warning

题目：实现 strStr() 函数。

给你两个字符串 haystack 和 needle ，请你在 haystack 字符串中找出 needle 字符串出现的第一个位置（下标从 0 开始）。如果不存在，则返回 -1 。
说明：

  1. 当 needle 是空字符串时，我们应当返回什么值呢？这是一个在面试中很好的问题。
  2. 对于本题而言，当 needle 是空字符串时我们应当返回 0 。这与 C 语言的 strstr() 以及 Java 的 indexOf() 定义相符。

示例 1：
输入：haystack = “hello”, needle = “ll”
输出：2

示例 2：
输入：haystack = “aaaaa”, needle = “bba”
输出：-1 :::

代码

public int strStr(String haystack, String needle) {
    char[] hayChars = haystack.toCharArray();
    char[] needChars = needle.toCharArray();

    int hayLen = hayChars.length;
    int needLen = needChars.length;

    // 构造 next 数组
    int[] next = new int[needLen];

    // 构造 next[], 让自己和自己对比
    for (int i = 1, j = 0; i < needLen; i++) {
        // 匹配不成功的话，j = next(j)
        while (j > 0 && needChars[j] != needChars[i]) j = next[j - 1];
        // 匹配成功的话，先让 j++
        if (needChars[i] == needChars[j]) j++;
        // 更新 next[i]，结束本次循环，i++
        next[i] = j;
    }
    // 匹配过程，i = 0，j = 0 开始，i 小于等于原串长度 【匹配 i 从 0 开始】
    for (int i = 0, j = 0; i < hayLen; i++) {
        // 匹配不成功 j = next(j)
        while (j > 0 && hayChars[i] != needChars[j]) j = next[j - 1];
        // 匹配成功的话，先让 j++，结束本次循环后 i++
        if (hayChars[i] == needChars[j]) j++;
        // 整一段匹配成功，直接返回下标
        if (j == needLen) return i - needLen + 1;
    }
    return -1;
}

public int strStr(String haystack, String needle) {
    char[] hayChars = haystack.toCharArray();
    char[] needChars = needle.toCharArray();

    int hayLen = hayChars.length;
    int needLen = needChars.length;

    for (int i = 0; i < hayLen; i++) {
        int a = i, b = 0;
        while (b < needLen && hayChars[a] == needChars[b]) {
            a++;
            b++;
        }
        if (b == needLen) return i;
    }
    return -1;
}