07 自动求导

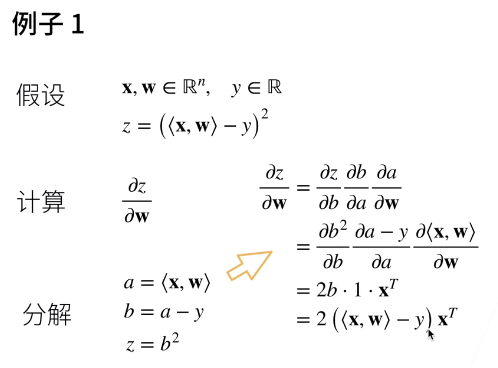
代码

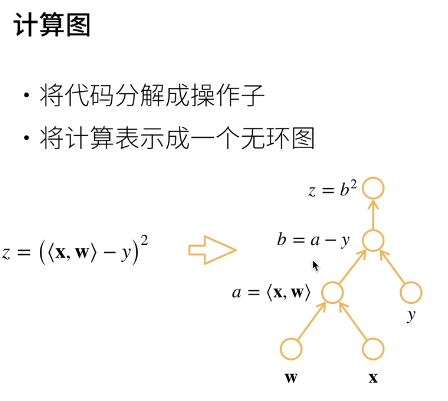
作为一个演示例子，假设我们想对函数关于列向量求导。首先，我们创建变量x并为其分配一个初始值。

import torch
x = torch.arange(4.0)
x

输出：

tensor([0., 1., 2., 3.])

#说明我需要一个地方存放x的梯度,x.grad 就可以访问了
x.requires_grad_(True)  # 等价于 `x = torch.arange(4.0, requires_grad=True)`
x.grad  # 默认值是None

y = 2 * torch.dot(x, x)
y

输出

tensor(28., grad_fn=<MulBackward0>)

函数关于的梯度应为。让我们快速验证我们想要的梯度是否正确计算。

x.grad == 4 * x

输出

tensor([True, True, True, True])

现在让我们计算x的另一个函数。

# 在默认情况下，PyTorch会累积梯度，我们需要清除之前的值
x.grad.zero_()
y = x.sum()
y.backward()
x.grad

x.sum()的导数全为1
输出

tensor([1., 1., 1., 1.])

当y不是标量时，向量y关于向量x的导数的最自然解释是一个矩阵。
对于高阶和高维的y和x，求导的结果可以是一个高阶张量。
然而，虽然这些更奇特的对象确实出现在高级机器学习中（包括深度学习中），
但当我们调用向量的反向计算时，
我们通常会试图计算一批训练样本中每个组成部分的损失函数的导数。
这里，我们的目的不是计算微分矩阵，而是批量中每个样本单独计算的偏导数之和。

# 对非标量调用`backward`需要传入一个`gradient`参数，该参数指定微分函数关于`self`的梯度。在我们的例子中，我们只想求偏导数的和，所以传递一个1的梯度是合适的
x.grad.zero_()
y = x * x
# 等价于y.backward(torch.ones(len(x)))
y.sum().backward()
x.grad

输出

tensor([0., 2., 4., 6.])

有时，我们希望将某些计算移动到记录的计算图之外。
例如，假设y是作为x的函数计算的，而z则是作为y和x的函数计算的。
现在，想象一下，我们想计算z关于x的梯度，
但由于某种原因，我们希望将y视为一个常数，
并且只考虑到x在y被计算后发挥的作用。

在这里，我们可以分离y来返回一个新变量u，
该变量与y具有相同的值，但丢弃计算图中如何计算y的任何信息。
换句话说，梯度不会向后流经u到x。
因此，下面的反向传播函数计算z=ux关于x的偏导数，
同时将u作为常数处理，而不是z=xx*x关于x的偏导数。

x.grad.zero_()
y = x * x
u = y.detach()
z = u * x
z.sum().backward()
x.grad == u

tensor([True, True, True, True])

由于记录了y的计算结果，我们可以随后在y上调用反向传播，
得到y=xx关于的x的导数，这里是2x。

x.grad.zero_()
y.sum().backward()
x.grad == 2 * x

tensor([True, True, True, True])

2.5.4. Python控制流的梯度计算

使用自动求导的一个好处是，
即使构建函数的计算图需要通过Python控制流（例如，条件、循环或任意函数调用），
我们仍然可以计算得到的变量的梯度。
在下面的代码中，while循环的迭代次数和if语句的结果都取决于输入a的值。

def f(a):
    b = a * 2
    while b.norm() < 1000:
        b = b * 2
    if b.sum() > 0:
        c = b
    else:
        c = 100 * b
    return c

让我们计算梯度。

a.grad == d / a

tensor(True)