503. 下一个更大元素 II

难度中等331
给定一个循环数组（最后一个元素的下一个元素是数组的第一个元素），输出每个元素的下一个更大元素。数字 x 的下一个更大的元素是按数组遍历顺序，这个数字之后的第一个比它更大的数，这意味着你应该循环地搜索它的下一个更大的数。如果不存在，则输出 -1。
示例 1:
输入: [1,2,1]
输出: [2,-1,2]
解释: 第一个 1 的下一个更大的数是 2；
数字 2 找不到下一个更大的数；
第二个 1 的下一个最大的数需要循环搜索，结果也是 2。

注意: 输入数组的长度不会超过 10000。

  1. class Solution {
  2. public:
  3.     vector<int> nextGreaterElements(vector<int>& nums) {
  4.         int n = nums.size();
  5.         vector<int> ans(n, -1);
  6.         stack<int> stk;
  7.         //从后往前找 只不过最后的n - 1数是用来模拟循环数组的
  8.         //2 * n - 1是n + n - 1,n - 1是前n - 1个数
  9.         for(int i = 2 * n - 1; i >= 0; -- i){
  10.             //构造一个严格单调递减的栈，每次入栈时，比它小的数都会被剔除
  11.             //相等的也得剔除掉，因为我们是求严格更大的，所以必须加上>=
  12.             while(!stk.empty() && nums[i % n] >= stk.top()){
  13.                 stk.pop();
  14.             }
  15.             //如果没找到更小的元素，那么就说明不存在
  16.             //i % n是用来表示循环数组
  17.             ans[i % n] = stk.empty() ? -1 : stk.top();
  18.             //加入比较行列
  19.             stk.push(nums[i % n]);
  20.         }
  21.         return ans;
  22.     }
  23. };

84. 柱状图中最大的矩形

难度困难1220
给定 n 个非负整数，用来表示柱状图中各个柱子的高度。每个柱子彼此相邻，且宽度为 1 。
求在该柱状图中，能够勾勒出来的矩形的最大面积。

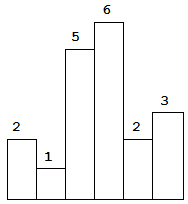
单调栈 - 图1
以上是柱状图的示例，其中每个柱子的宽度为 1，给定的高度为 [2,1,5,6,2,3]。

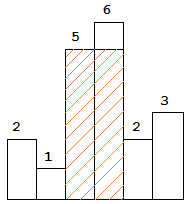
单调栈 - 图2
图中阴影部分为所能勾勒出的最大矩形面积，其面积为 10 个单位。

示例:
输入: [2,1,5,6,2,3]
输出: 10

  1. class Solution {
  2. public:
  3.     int largestRectangleArea(vector<int>& heights) {
  4.         int n = heights.size();
  5.         int ans = 0;
  6.         vector<int> sl(n, -1), sr(n, n);
  7.         stack<int> stk;
  8.         //从暴力算法衍生，左右都找到最近的高度小于当前值的柱子
  9.         //求下一个最小，也就是往右看不满足条件的第一个值 即小于当前高度的最近值
  10.         //构造了一个单调递增栈 栈顶当前是最大 更大都被去掉了
  11.         for(int i = n - 1; i >= 0; -- i){
  12.             while(!stk.empty() && heights[i] <= heights[stk.top()]){
  13.                 stk.pop();
  14.             }
  15.             sr[i] = stk.empty() ? n : stk.top();
  16.             stk.push(i);
  17.         }
  18.         while(!stk.empty()) stk.pop();
  19.         //求上一个最大，往左看不满足的第一个值
  20.         for(int i = 0; i < n; ++ i){
  21.             while(!stk.empty() && heights[i] <= heights[stk.top()]){
  22.                 stk.pop();
  23.             }
  24.             sl[i] = stk.empty() ? -1 : stk.top();
  25.             stk.push(i);
  26.         }
  27.         for(int i = 0; i < n; ++ i){
  28.             int width = sr[i] - sl[i] - 1;
  29.             ans = max(ans, width * heights[i]);
  30.         }
  31.         return ans;
  32.     }
  33. };

优化

  1. class Solution {
  2. public:
  3.     int largestRectangleArea(vector<int>& heights) {
  4.         int n = heights.size();
  5.         int ans = 0;
  6.         vector<int> sl(n, -1), sr(n, n);
  7.         stack<int> stk;
  8.         //从暴力算法衍生，左右都找到最近的高度小于当前值的柱子
  9.         //求下一个最小，也就是往右看不满足条件的第一个值 即小于当前高度的最近值
  10.         //构造了一个单调递增栈 栈顶当前是最大 更大都被去掉了
  11.         for(int i = 0; i < n; ++ i){
  12.             while(!stk.empty() && heights[i] <= heights[stk.top()]){
  13.                 sr[stk.top()] = i;
  14.                 stk.pop();
  15.             }
  16.             sl[i] = stk.empty() ? -1 : stk.top();
  17.             stk.push(i);
  18.         }
  19.         for(int i = 0; i < n; ++ i){
  20.             int width = sr[i] - sl[i] - 1;
  21.             ans = max(ans, width * heights[i]);
  22.         }
  23.         return ans;
  24.     }
  25. };

456. 132 模式

难度中等383
给你一个整数数组 nums ，数组中共有 n 个整数。132 模式的子序列 由三个整数 nums[i]、nums[j] 和 nums[k] 组成，并同时满足：i < j < k 和 nums[i] < nums[k] < nums[j] 。
如果 nums 中存在 132 模式的子序列 ，返回 true ；否则，返回 false 。

进阶：很容易想到时间复杂度为 O(n^2) 的解决方案，你可以设计一个时间复杂度为 O(n logn) 或 O(n) 的解决方案吗？

示例 1：
输入：nums = [1,2,3,4]
输出：false
解释：序列中不存在 132 模式的子序列。

示例 2：
输入：nums = [3,1,4,2]
输出：true
解释：序列中有 1 个 132 模式的子序列： [1, 4, 2] 。

示例 3：
输入：nums = [-1,3,2,0]
输出：true
解释：序列中有 3 个 132 模式的的子序列：[-1, 3, 2]、[-1, 3, 0] 和 [-1, 2, 0] 。


提示：

  • n == nums.length
  • 1 <= n <= 104

  • -109 <= nums[i] <= 109

    1. class Solution {
    2. public:
    3.   bool find132pattern(vector<int>& nums) {
    4.       stack<int> stk;
    5.       int k = INT_MIN;
    6.       int n = nums.size();
    7.       //保持单调栈是单调递减的 
    8.       //也就是保持nums从后往前是单调递减的
    9.       //同时我们检测 因为不是单调递减而弹出一个j值，用一个k值来维护栈顶后的最大值
    10.       //只要往前的时候存在一个i值比k值小，而且k值还不在栈中，那么就满足条件
    11.       //i-1 j-3 k-2
    12.       //i是遍历保存，k是存值保存， j是栈顶保存
    13.       for(int i = n - 1; i >= 0; -- i){
    14.           if(nums[i] < k) return true;
    15.           while(!stk.empty() && stk.top() < nums[i]){
    16.               k = max(k, stk.top());
    17.               stk.pop();
    18.           }
    19.           stk.push(nums[i]);
    20.       }
    21.       return false;
    22.   }
    23. };

    1124. 表现良好的最长时间段

    总结

  • 从后往前，当前遍历值>= 栈顶 时弹栈 -> 栈单调递增（栈顶到栈底），可用来求当前元素右边的第一个比它大的元素。

  • 从后往前，当前遍历值 <= 栈顶 时弹栈 -> 栈单调递减（栈顶到栈底），可用来求当前元素右边的第一个比它小的元素。
  • 从前往后，当前遍历值>= 栈顶 时弹栈 -> 栈单调递增（栈顶到栈底），可用来求当前元素左边的第一个比它大的元素。
  • 从前往后，当前遍历值 <= 栈顶 时弹栈 -> 栈单调递减（栈顶到栈底），可用来求当前元素左边的第一个比它小的元素。