总结&&模版

l的初始值由理论上的最小值决定，r的初始值可以由数值范围上界决定，也可以由数组最大值决定。
至于while结束的判定条件是用 < 还是<=，这点可以确定长期使用一种统一的方式。
<结束的条件就是left == right ,搜索的区间是[left,right)，注意在更换上下界的时候不能都+ -
<=结束的条件就是left = right + 1，搜索区间是[left, right], 更换上下界的时候应当同时+ -
更换上下界时的区别也就是当前的值是已经搜索过还是没有搜索过。
建议还是统一用<的方式，判断二分左端点还是右端点再写，不容易出错。
二分查找的是一个值，他的左边满足某种性质，右边不满足该性质。
两个模版的差别再说找的是夹在中间的哪一个具体值。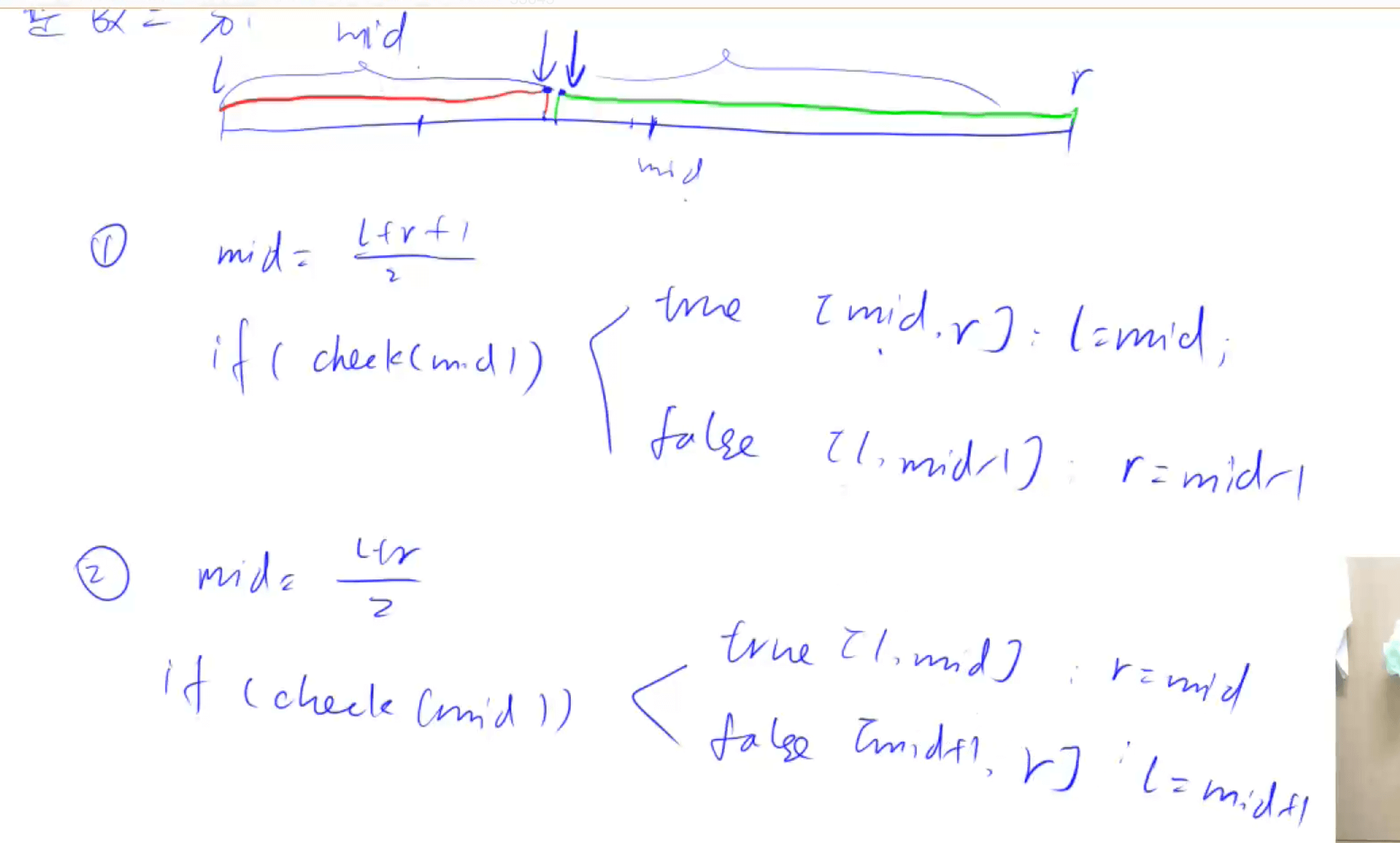
image.png

  1. //查找左端点（红色，端点的左边都满足红色性质，check红色性质)
  2. int SL(int l, int r) 
  3. {
  4.     while (l < r)
  5.     {                   
  6.         int mid = l + r + 1 >> 1; //需要+1 防止死循环
  7.         if (check(mid)) l = mid;
  8.         else r = mid - 1; 
  9.     }
  10.     return l; 
  11. }
  12. //查找右端点（绿色，端点的右边都满足绿色性质，check绿色性质）
  13. int SR(int l, int r)
  14. {
  15.     while (l < r)
  16.     {
  17.         int mid = l + r >> 1;
  18.         if (check(mid)) r = mid; 
  19.         else l = mid + 1; 
  20.     }   
  21.     return r;
  22.  // 最后r=l
  23. }

23. 合并K个升序链表

难度困难1142
给你一个链表数组，每个链表都已经按升序排列。
请你将所有链表合并到一个升序链表中，返回合并后的链表。

示例 1：
输入：lists = [[1,4,5],[1,3,4],[2,6]]
输出：[1,1,2,3,4,4,5,6]
解释：链表数组如下：
[
1->4->5,
1->3->4,
2->6
]
将它们合并到一个有序链表中得到。
1->1->2->3->4->4->5->6

示例 2：
输入：lists = []
输出：[]

示例 3：
输入：lists = [[]]
输出：[]


提示：

  • k == lists.length
  • 0 <= k <= 10^4
  • 0 <= lists[i].length <= 500
  • -10^4 <= lists[i][j] <= 10^4
  • lists[i] 按 升序 排列

  • lists[i].length 的总和不超过 10^4

    1. /**
    2. * Definition for singly-linked list.
    3. * struct ListNode {
    4. *     int val;
    5. *     ListNode *next;
    6. *     ListNode() : val(0), next(nullptr) {}
    7. *     ListNode(int x) : val(x), next(nullptr) {}
    8. *     ListNode(int x, ListNode *next) : val(x), next(next) {}
    9. * };
    10. */
    11. class Solution {
    12. public:
    13.   ListNode* mergeTwoLists(ListNode* a, ListNode* b){
    14.       if((!a) || (!b)) return a ? a : b;
    15.       ListNode* nhead = new ListNode(-1);
    16.       ListNode* pre = nhead;
    17.       ListNode* ap = a, *bp = b;
    18.       while(ap && bp){
    19.           if(ap->val < bp->val){
    20.               pre->next = ap;
    21.               ap = ap->next;
    22.           }else{
    23.               pre->next = bp;
    24.               bp = bp->next;
    25.           }
    26.           pre = pre->next;
    27.       }
    28.       pre->next = ap == nullptr ? bp : ap;
    29.       return nhead->next;
    30.   }
    31.   ListNode* merge(vector<ListNode*>& lists, int l, int r){
    32.       //只有一个元素的情况
    33.       if(l == r) return lists[l];
    34.       if(l > r) return nullptr;
    35.       int mid = l + r >> 1;
    36.       return mergeTwoLists(merge(lists, l, mid), merge(lists, mid + 1, r));
    38.   }
    39.   ListNode* mergeKLists(vector<ListNode*>& lists) {
    40.       return merge(lists, 0, lists.size() - 1);
    41.   }
    42. };

最大化最小值，或者最小化最大值，直接用二分法

1760. 袋子里最少数目的球

难度中等14
给你一个整数数组 nums ，其中 nums[i] 表示第 i 个袋子里球的数目。同时给你一个整数 maxOperations 。
你可以进行如下操作至多 maxOperations 次：

  • 选择任意一个袋子，并将袋子里的球分到 2 个新的袋子中，每个袋子里都有正整数 个球。
    • 比方说，一个袋子里有 5 个球，你可以把它们分到两个新袋子里，分别有 1 个和 4 个球，或者分别有 2 个和 3 个球。

你的开销是单个袋子里球数目的 最大值 ，你想要 最小化 开销。
请你返回进行上述操作后的最小开销。

示例 1：
输入：nums = [9], maxOperations = 2
输出：3
解释：
- 将装有 9 个球的袋子分成装有 6 个和 3 个球的袋子。[9] -> [6,3] 。
- 将装有 6 个球的袋子分成装有 3 个和 3 个球的袋子。[6,3] -> [3,3,3] 。
装有最多球的袋子里装有 3 个球，所以开销为 3 并返回 3 。

示例 2：
输入：nums = [2,4,8,2], maxOperations = 4
输出：2
解释：
- 将装有 8 个球的袋子分成装有 4 个和 4 个球的袋子。[2,4,8,2] -> [2,4,4,4,2] 。
- 将装有 4 个球的袋子分成装有 2 个和 2 个球的袋子。[2,4,4,4,2] -> [2,2,2,4,4,2] 。
- 将装有 4 个球的袋子分成装有 2 个和 2 个球的袋子。[2,2,2,4,4,2] -> [2,2,2,2,2,4,2] 。
- 将装有 4 个球的袋子分成装有 2 个和 2 个球的袋子。[2,2,2,2,2,4,2] -> [2,2,2,2,2,2,2,2] 。
装有最多球的袋子里装有 2 个球，所以开销为 2 并返回 2 。

示例 3：
输入：nums = [7,17], maxOperations = 2
输出：7
提示：

  • 1 <= nums.length <= 105
  • 1 <= maxOperations, nums[i] <= 109
    1. class Solution {
    2.   typedef long long ll;
    3. public:
    4.   bool check(int mid, vector<int>& nums, int maxOperations){
    5.       int res = 0;
    6.       for(auto& cur : nums){
    7.           //最小化最大值问题
    8.           //原问题：最多分maxOperations次，使得最终每堆个数不超过mid个
    9.           //cur  / mid 上取整，等于(cur + mid - 1) / mid 下取整
    10.           //-1是最后一堆，不用分割的，已经成一堆
    11.           //转化为 求的是最少多少次，能使得球的个数小于等于mid
    12.           res += (cur + mid - 1) / mid - 1;
    13.           if(res > maxOperations) return false;
    14.       }
    15.       return true;
    16.   }
    17.   int minimumSize(vector<int>& nums, int maxOperations) {
    18.       //定制左右边界
    19.       ll l = 1, r = 1e9;
    20.       ll ans = 0;
    21.       while(l < r){
    22.           int mid = l + r >> 1;
    23.           //左边区间及本身满足
    24.           if(check(mid, nums, maxOperations)){
    25.               r = mid;
    26.           }else{
    27.               l = mid + 1;
    28.           }
    29.       }
    30.       return r;
    31.   }
    32. };

5219. 每个小孩最多能分到多少糖果

基本思路与1760相同，唯一的不同是上下界判定和处理方式。

395. 至少有 K 个重复字符的最长子串

难度中等430
给你一个字符串 s 和一个整数 k ，请你找出 s 中的最长子串， 要求该子串中的每一字符出现次数都不少于 k 。返回这一子串的长度。

示例 1：
输入：s = “aaabb”, k = 3
输出：3
解释：最长子串为 “aaa” ，其中 ‘a’ 重复了 3 次。

示例 2：
输入：s = “ababbc”, k = 2
输出：5
解释：最长子串为 “ababb” ，其中 ‘a’ 重复了 2 次， ‘b’ 重复了 3 次。

对于字符串 ss，如果存在某个字符 \textit{ch}ch，它的出现次数大于 00 且小于 kk，则任何包含 \textit{ch}ch 的子串都不可能满足要求。也就是说，我们将字符串按照 \textit{ch}ch 切分成若干段，则满足要求的最长子串一定出现在某个被切分的段内，而不能跨越一个或多个段。因此，可以考虑分治的方式求解本题。

  1. class Solution {
  2. public:
  3.     int check(const string s, int l, int r, int k){
  4.         //计数
  5.         vector<int> cnt(26, 0);
  6.         for(int i = l; i <= r; ++ i){
  7.             cnt[s[i] - 'a'] ++;
  8.         }
  9.         //得到当前二分的分界点
  10.         char split = 0;
  11.         for(int i = 0; i < 26; ++ i){
  12.             //不满足题目的条件
  13.             if(cnt[i] > 0 && cnt[i] < k){
  14.                 split = 'a' + i;
  15.                 break;
  16.             }
  17.         }
  18.         //没找到 那么整个都满足
  19.         if(split == 0){
  20.             return r - l + 1;
  21.         }
  22.         int i = l;
  23.         int res = 0;
  24.         while(i <= r){
  25.             //找到分界点的第一段 这段是不满足题意的
  26.             while(i <= r && s[i] == split){
  27.                 i ++;
  28.             }
  29.             //临界情况 到最后了
  30.             if(i > r){
  31.                 break;
  32.             }
  33.             //从现在开始满足直到下一个该数
  34.             int start = i;
  35.             while(i <= r && s[i] != split){
  36.                 i ++;
  37.             }
  38.             int len = check(s, start, i - 1, k);
  39.             res = max(res, len);
  40.         }
  41.         return res;
  42.     }
  43.     int longestSubstring(string s, int k) {
  44.         int n = s.size();
  45.         return check(s, 0, n - 1, k);
  46.     }
  47. };

5711. 有界数组中指定下标处的最大值

难度中等5
给你三个正整数 n、index 和 maxSum 。你需要构造一个同时满足下述所有条件的数组 nums（下标 从 0 开始 计数）：

  • nums.length == n
  • nums[i] 是 正整数 ，其中 0 <= i < n
  • abs(nums[i] - nums[i+1]) <= 1 ，其中 0 <= i < n-1
  • nums 中所有元素之和不超过 maxSum
  • nums[index] 的值被 最大化

返回你所构造的数组中的 nums[index] 。
注意：abs(x) 等于 x 的前提是 x >= 0 ；否则，abs(x) 等于 -x 。

示例 1：
输入：n = 4, index = 2, maxSum = 6
输出：2
解释：数组 [1,1,2,1] 和 [1,2,2,1] 满足所有条件。不存在其他在指定下标处具有更大值的有效数组。

示例 2：
输入：n = 6, index = 1, maxSum = 10
输出：3


提示：

  • 1 <= n <= maxSum <= 109

  • 0 <= index < n

    1. using ll = long long;
    2. class Solution {
    3. public:
    4.   bool check(ll mid, ll n, ll index, ll maxSum){
    5.       //mid表示的是index处的数字，我们要算出这个位置的最大数字
    6.       ll res = 0;
    7.       //表示左右分别能放的数字个数 这里的index不是坐标 是数
    8.       ll lnum = index + 1, rnum = n - index;
    9.       //算左边和 包括mid本身
    10.       //如果能完美递减数列那么就放进去 等差数列公式计算/求和公式 左边mid + 1项
    11.       if(mid - lnum >= 1){
    12.           res += lnum * (mid + mid - lnum + 1) / 2;
    13.       }else{
    14.           //分类加起来
    15.           res += mid * (mid + 1) / 2 + lnum - mid;
    16.       }
    17.       //计算右边
    18.       if(mid - rnum >= 1){
    19.           res += rnum * (mid + mid - rnum + 1) / 2;
    20.       }else{
    21.           res += mid * (mid+ 1) / 2 + rnum - mid;
    22.       }
    23.       res -= mid;
    24.       return res <= maxSum;
    25.   }
    26.   int maxValue(int n, int index, int maxSum) {
    27.       ll l = 1, r = 1e9;
    28.       while(l < r){
    29.           ll mid = l + r + 1 >> 1;
    30.           if(check(mid, n, index, maxSum)){
    31.               l = mid;
    32.           }else{
    33.               r = mid - 1;
    34.           }
    35.       }
    36.       return l;
    37.   }
    38. };

    74. 搜索二维矩阵

    难度中等391
    编写一个高效的算法来判断 m x n 矩阵中，是否存在一个目标值。该矩阵具有如下特性：

  • 每行中的整数从左到右按升序排列。

  • 每行的第一个整数大于前一行的最后一个整数。


    示例 1：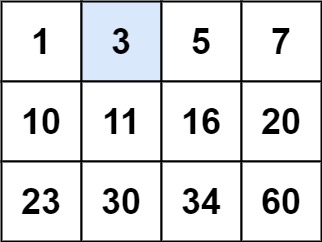
    分治法/二分法-应用 - 图2
    输入：matrix = [[1,3,5,7],[10,11,16,20],[23,30,34,60]], target = 3
    输出：true

示例 2：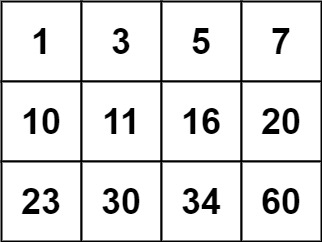
分治法/二分法-应用 - 图3
输入：matrix = [[1,3,5,7],[10,11,16,20],[23,30,34,60]], target = 13
输出：false


提示：

  • m == matrix.length
  • n == matrix[i].length
  • 1 <= m, n <= 100
  • -104 <= matrix[i][j], target <= 104
    1. class Solution {
    2. public:
    3.   bool searchMatrix(vector<vector<int>>& matrix, int target) {
    4.       int n = matrix.size();
    5.       if(!n) return false;
    6.       int m = matrix[0].size();
    7.       if(!m) return false;
    8.       int l = 0, r = n * m - 1;
    9.       while(l <= r){
    10.           int mid = l + r >> 1;
    11.           int row = mid / m, col = mid % m;
    12.           if(target == matrix[row][col]){
    13.               return true;
    14.           }else if(target > matrix[row][col]){
    15.               l = mid + 1;
    16.           }else{
    17.               r = mid - 1;
    18.           }
    19.       }
    20.       return false;
    21.   }
    22. };

    33. 搜索旋转排序数组

    难度中等1288
    整数数组 nums 按升序排列，数组中的值 互不相同 。
    在传递给函数之前，nums 在预先未知的某个下标 k（0 <= k < nums.length）上进行了 旋转，使数组变为 [nums[k], nums[k+1], ..., nums[n-1], nums[0], nums[1], ..., nums[k-1]]（下标 从 0 开始 计数）。例如， [0,1,2,4,5,6,7] 在下标 3 处经旋转后可能变为 [4,5,6,7,0,1,2] 。
    给你 旋转后 的数组 nums 和一个整数 target ，如果 nums 中存在这个目标值 target ，则返回它的下标，否则返回 -1 。

    示例 1：
    输入：nums = [4,5,6,7,0,1,2], target = 0
    输出：4

示例 2：
输入：nums = [4,5,6,7,0,1,2], target = 3
输出：-1
示例 3：
输入：nums = [1], target = 0
输出：-1


提示：

  • 1 <= nums.length <= 5000
  • -10^4 <= nums[i] <= 10^4
  • nums 中的每个值都 独一无二
  • 题目数据保证 nums 在预先未知的某个下标上进行了旋转

  • -10^4 <= target <= 10^4


    进阶：你可以设计一个时间复杂度为 O(log n) 的解决方案吗？

    1. class Solution {
    2. public:
    3.   int search(vector<int>& nums, int target) {
    4.       int n = nums.size();
    5.       if(!n) return -1;
    6.       int l = 0, r = n - 1;
    7.       while(l <= r){
    8.           int mid = l + r >> 1;
    9.           if(nums[mid] == target){
    10.               return mid;
    11.           }
    12.           if(nums[0] <= nums[mid]){
    13.               if(target >= nums[0] && nums[mid] > target){
    14.                   r = mid - 1;
    15.               }else{
    16.                   l = mid + 1;
    17.               }
    18.           }else{
    19.               if(target <= nums[n - 1] && nums[mid] < target){
    20.                   l = mid + 1;
    21.               }else{
    22.                   r = mid - 1;
    23.               }
    24.           }
    25.       }
    26.       return -1;
    27.   }
    28. };

    81. 搜索旋转排序数组 II

    难度中等367
    已知存在一个按非降序排列的整数数组 nums ，数组中的值不必互不相同。
    在传递给函数之前，nums 在预先未知的某个下标 k（0 <= k < nums.length）上进行了 旋转 ，使数组变为 [nums[k], nums[k+1], ..., nums[n-1], nums[0], nums[1], ..., nums[k-1]]（下标 从 0 开始 计数）。例如， [0,1,2,4,4,4,5,6,6,7] 在下标 5 处经旋转后可能变为 [4,5,6,6,7,0,1,2,4,4] 。
    给你 旋转后 的数组 nums 和一个整数 target ，请你编写一个函数来判断给定的目标值是否存在于数组中。如果 nums 中存在这个目标值 target ，则返回 true ，否则返回 false 。

    示例 1：
    输入：nums = [2,5,6,0,0,1,2], target = 0
    输出：true

示例 2：
输入：nums = [2,5,6,0,0,1,2], target = 3
输出：false

提示：

  • 1 <= nums.length <= 5000
  • -104 <= nums[i] <= 104
  • 题目数据保证 nums 在预先未知的某个下标上进行了旋转

  • -104 <= target <= 104


    进阶：

  • 这是 搜索旋转排序数组 的延伸题目，本题中的 nums 可能包含重复元素。

  • 这会影响到程序的时间复杂度吗？会有怎样的影响，为什么？

    1. class Solution {
    2. public:
    3.   bool search(vector<int>& nums, int target) {
    4.       int n = nums.size();
    5.       if(n == 1) return nums[0] == target;
    6.       int l = 0, r = n - 1;
    7.       while(l <= r){
    8.       //移动边界到不重复的地方
    9.           while(l < r && nums[l] == nums[l + 1]) ++ l;
    10.           while(l < r && nums[r] == nums[r - 1]) -- r;
    11.           int mid = l + r >> 1;
    12.           if(nums[mid] == target) return true;
    13.           if(nums[l] <= nums[mid]){
    14.               if(target >= nums[l] && nums[mid] > target){
    15.                   r = mid - 1;
    16.               }else{
    17.                   l = mid + 1;
    18.               }
    19.           }else{
    20.               if(target <= nums[n - 1] && nums[mid] < target){
    21.                   l = mid + 1;
    22.               }else{
    23.                   r = mid - 1;
    24.               }
    25.           }
    26.       }
    27.       return false;
    28.   }
    29. };

    比较好的解决重复元素的方法

    1. class Solution {
    2. public:
    3.   bool search(vector<int>& nums, int target) {
    4.       int n = nums.size();
    5.       if(n == 1) return nums[0] == target;
    6.       int l = 0, r = n - 1;
    7.       while(l <= r){
    8.           int mid = l + r >> 1;
    9.           if(nums[mid] == target) return true;
    10.           if(nums[l] == nums[mid] && nums[mid] == nums[r]){
    11.               l ++;
    12.               r --;
    13.           }
    14.           else if(nums[l] <= nums[mid]){
    15.               if(target >= nums[l] && nums[mid] > target){
    16.                   r = mid - 1;
    17.               }else{
    18.                   l = mid + 1;
    19.               }
    20.           }else{
    21.               if(target <= nums[n - 1] && nums[mid] < target){
    22.                   l = mid + 1;
    23.               }else{
    24.                   r = mid - 1;
    25.               }
    26.           }
    27.       }
    28.       return false;
    29.   }
    30. };

    153. 寻找旋转排序数组中的最小值

    难度中等427
    已知一个长度为 n 的数组，预先按照升序排列，经由 1 到 n 次 旋转 后，得到输入数组。例如，原数组 nums = [0,1,2,4,5,6,7] 在变化后可能得到：

  • 若旋转 4 次，则可以得到 [4,5,6,7,0,1,2]

  • 若旋转 7 次，则可以得到 [0,1,2,4,5,6,7]

注意，数组 [a[0], a[1], a[2], ..., a[n-1]] 旋转一次 的结果为数组 [a[n-1], a[0], a[1], a[2], ..., a[n-2]] 。
给你一个元素值 互不相同 的数组 nums ，它原来是一个升序排列的数组，并按上述情形进行了多次旋转。请你找出并返回数组中的 最小元素 。

示例 1：
输入：nums = [3,4,5,1,2]
输出：1
解释：原数组为 [1,2,3,4,5] ，旋转 3 次得到输入数组。

示例 2：
输入：nums = [4,5,6,7,0,1,2]
输出：0
解释：原数组为 [0,1,2,4,5,6,7] ，旋转 4 次得到输入数组。

示例 3：
输入：nums = [11,13,15,17]
输出：11
解释：原数组为 [11,13,15,17] ，旋转 4 次得到输入数组。


提示：

  • n == nums.length
  • 1 <= n <= 5000
  • -5000 <= nums[i] <= 5000
  • nums 中的所有整数 互不相同
  • nums 原来是一个升序排序的数组，并进行了 1 至 n 次旋转
    1. class Solution {
    2. public:
    3.   int findMin(vector<int>& nums) {
    4.       int n = nums.size();
    5.       int l = 0, r = n - 1;
    6.       while(l < r){
    7.           int mid = l + r >> 1;
    8.           if(nums[mid] <= nums[r]){
    9.               r = mid;
    10.           }else if(nums[mid] > nums[r]){
    11.               l = mid + 1;
    12.           }
    13.       }
    14.       return nums[l];
    15.   }
    16. };
    如果要求最大的数
    其实就是二分的两种情况，一种是左包含，一种是右包含
    1. class Solution {
    2. public:
    3.   int findMin(vector<int>& nums) {
    4.       int n = nums.size();
    5.       int l = 0, r = n - 1;
    6.       while(l < r){
    7.           int mid = l + r >> 1;
    8.           if(nums[mid] >= nums[l]){
    9.               l = mid;
    10.           }else if(nums[mid] < nums[l]){
    11.               r = mid - 1;
    12.           }
    13.       }
    14.       return nums[l];
    15.   }
    16. };

    154. 寻找旋转排序数组中的最小值 II

    难度困难277
    就是带上重复元素的版本
    与之前的解决方法类似
    1. class Solution {
    2. public:
    3.   int findMin(vector<int>& nums) {
    4.       int n = nums.size();
    5.       int l = 0, r = n - 1;
    6.       while(l < r){
    7.           int mid = l + r >> 1;
    8.           if(nums[mid] == nums[l] && nums[mid] == nums[r]){
    9.               ++ l;
    10.               -- r;
    11.           }
    12.           else if(nums[mid] <= nums[r]){
    13.               r = mid;
    14.           }else{
    15.               l = mid + 1;
    16.           }
    17.       }
    18.       return nums[l];
    19.   }
    20. };