搜索型-基于暴力剪枝-DFS/BFS/回溯/记忆化

LC22 LC46

22. 括号生成

难度中等1542
数字 n 代表生成括号的对数，请你设计一个函数，用于能够生成所有可能的并且 有效的 括号组合。

class Solution {
public:
    void backTrack(int left, int right, string& res, vector<string>& ans){
        if(left == 0 && right == 0){
            ans.push_back(res);
            return;
        }
        if(left > 0){
            res += '(';
            backTrack(left - 1, right, res, ans);
            res.pop_back();
        }
        if(right > left){
            res += ')';
            backTrack(left, right - 1, res, ans);
            res.pop_back();
        }
    }
    vector<string> generateParenthesis(int n) {
        vector<string> ans;
        string res;
        backTrack(n, n, res, ans);
        return ans;
    }
};

或者

class Solution {
public:
    void backTrack(int left, int right, string res, vector<string>& ans){
        if(left == 0 && right == 0){
            ans.push_back(res);
            return;
        }
        if(left > 0){
            backTrack(left - 1, right, res + '(', ans);
        }
        if(right > left){
            backTrack(left, right - 1, res + ')', ans);
        }
    }
    vector<string> generateParenthesis(int n) {
        vector<string> ans;
        string res;
        backTrack(n, n, res, ans);
        return ans;
    }
};

46. 全排列

难度中等1122
给定一个 没有重复 数字的序列，返回其所有可能的全排列。
示例:
输入: [1,2,3]
输出:
[
[1,2,3],
[1,3,2],
[2,1,3],
[2,3,1],
[3,1,2],
[3,2,1]
]

为什么要使用visited，因为只有使用了visited，才能保证是没有重复的，否则可能会出现输出的数字有重复的情况。

class Solution {
public:
    vector<int> visited;
    void backTrack(vector<vector<int> >& ans, vector<int>& res, int begin, int len, vector<int>& visited, const vector<int> nums){
        if(begin == len){
            ans.push_back(res);
            return;
        }
        for(int j = 0; j < len; ++ j){
            if(!visited[j]){
                visited[j] = 1;
                res.push_back(nums[j]);
                backTrack(ans, res, begin + 1, len, visited, nums);
                res.pop_back();
                visited[j] = 0;
            }
        }
    }
    vector<vector<int>> permute(vector<int>& nums) {
        int n = nums.size();
        vector<vector<int> > ans;
        vector<int> res;
        vector<int> visited(n, 0);
        this->visited = visited;
        backTrack(ans, res, 0, n, visited, nums);
        return ans;
    }
};

17. 电话号码的字母组合

难度中等1125
给定一个仅包含数字 2-9 的字符串，返回所有它能表示的字母组合。答案可以按 任意顺序 返回。
给出数字到字母的映射如下（与电话按键相同）。注意 1 不对应任何字母。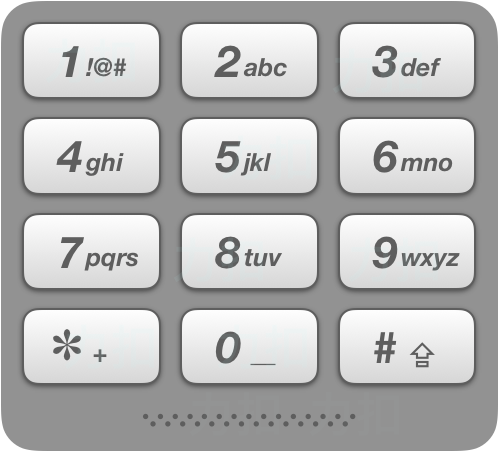


示例 1：
输入：digits = “23”
输出：[“ad”,”ae”,”af”,”bd”,”be”,”bf”,”cd”,”ce”,”cf”]

示例 2：
输入：digits = “”
输出：[]

示例 3：
输入：digits = “2”
输出：[“a”,”b”,”c”]
提示：

• 0 <= digits.length <= 4
• digits[i] 是范围 ['2', '9'] 的一个数字。

为什么这种情况就不要visited了？因为各个字符之间是相互独立的，其实是相当于产生了新的对象，不会有不同的字符映射同一个字符的情况。

class Solution {
public:
    void backTrack(unordered_map<char, string>& phnum, string& res, int begin, int len, vector<string>& ans, const string& digits){
        if(begin == len){
            ans.push_back(res);
            return;
        }
        char letters = digits[begin];
        for(auto& let: phnum[letters]){
            res.push_back(let);
            backTrack(phnum, res, begin + 1, len, ans, digits);
            res.pop_back();
        }
    }
    vector<string> letterCombinations(string digits) {
        vector<string> ans;
        string res;
        int n = digits.size();
        if(!n) return ans;
        unordered_map<char, string> phnum{
            {'2', "abc"},
            {'3', "def"},
            {'4', "ghi"},
            {'5', "jkl"},
            {'6', "mno"},
            {'7', "pqrs"},
            {'8', "tuv"},
            {'9', "wxyz"}
        };
        backTrack(phnum, res, 0, n, ans, digits);
        return ans;
    }
};

39. 组合总和

难度中等1160
给定一个无重复元素的数组 candidates 和一个目标数 target ，找出 candidates 中所有可以使数字和为 target 的组合。
candidates 中的数字可以无限制重复被选取。
说明：

• 所有数字（包括 target）都是正整数。
• 解集不能包含重复的组合。

示例 1：
输入：candidates = [2,3,6,7],target = 7,
所求解集为：
[
[7],
[2,2,3]
]

示例 2：
输入：candidates = [2,3,5],target = 8,
所求解集为：
[
[2,2,2,2],
[2,3,3],
[3,5]
]
提示：

• 1 <= candidates.length <= 30
• 1 <= candidates[i] <= 200
• candidate 中的每个元素都是独一无二的。
• 1 <= target <= 500

这题就是回溯，有个关键的去重就是用begin idx来记录，每次不重复扫描前面的数，类似于三数之和的做法。
如果不去重就是求全排列等的做法
如果不能使用重复的就要用used数组记录

class Solution {
public:
    vector<vector<int> > ans;
    void backtrack(int sum, int target, vector<int>& res, const vector<int>& candidates, int begin){
        if(sum == target){
            ans.push_back(res);
            return ;
        }
        if(sum > target) return ;
        //去重关键，这里从begin开始
        for(int i = begin; i < candidates.size(); ++ i){
            res.push_back(candidates[i]);
            //去重的关键，这里用
            backtrack(sum + candidates[i], target, res, candidates, i);
            res.pop_back();
        }
    }
    vector<vector<int>> combinationSum(vector<int>& candidates, int target) {
        int n = candidates.size();
        vector<int> res;
        backtrack(0, target, res, candidates, 0);
        return ans;
    }
};

55. 跳跃游戏

难度中等1053
给定一个非负整数数组 nums ，你最初位于数组的 第一个下标 。
数组中的每个元素代表你在该位置可以跳跃的最大长度。
判断你是否能够到达最后一个下标。

示例 1：
输入：nums = [2,3,1,1,4]
输出：true
解释：可以先跳 1 步，从下标 0 到达下标 1, 然后再从下标 1 跳 3 步到达最后一个下标。

示例 2：
输入：nums = [3,2,1,0,4]
输出：false
解释：无论怎样，总会到达下标为 3 的位置。但该下标的最大跳跃长度是 0 ， 所以永远不可能到达最后一个下标。
提示：

• 1 <= nums.length <= 3 * 10
• 0 <= nums[i] <= 10<br />

  class Solution {
  public:
    bool backTrack(int now, int end, const vector<int>& nums, vector<bool>& visited){
        if(now == end){
            return true;
        }
        int dis = min(end - now, nums[now]);
        visited[now] = 1;
        for(int i = 1; i <= dis; ++ i){
            if(!visited[now + i]){
                if(backTrack(now + i, end, nums, visited))
                    return true;
            }
        }
        return false;
    }
    bool canJump(vector<int>& nums) {
        int n = nums.size();
        vector<bool> visited(n, 0);
        return backTrack(0, n - 1, nums, visited);
    }
  };

  回溯+记忆化搜索，回溯无法过。