145. 二叉树的后序遍历

难度中等550
给定一个二叉树，返回它的 后序 遍历。
示例:
输入: [1,null,2,3]
1
\
2
/
3

输出: [3,2,1]
进阶: 递归算法很简单，你可以通过迭代算法完成吗？

145-1.后序遍历非递归

  1. class Solution {
  2. public:
  3.     vector<int> postorderTraversal(TreeNode* root) {
  4.         vector<int> ans;
  5.         if(root == nullptr) return ans;
  6.         stack<TreeNode* > stk;
  7.         TreeNode* prev = nullptr;
  8.         while(!stk.empty() || root != nullptr){
  9.             while(root != nullptr){
  10.                 stk.push(root);
  11.                 root = root->left;
  12.             }
  13.             root = stk.top();
  14.             stk.pop();
  15.             //root->right = prev的情况是当前root是某个父结点，且左右子结点都已经遍历完毕
  16.             //1.遍历到子节点 ｜｜ 2.子树已经遍历完了，根节点进入
  17.             if(root->right == nullptr || root->right == prev){
  18.                 ans.push_back(root->val);
  19.                 prev = root;
  20.                 root = nullptr;
  21.             }else{//有右节点就先遍历右节点
  22.                 stk.push(root);
  23.                 root = root->right;
  24.             }
  25.         }
  26.         return ans;
  27.     }
  28. };

145-2.中序遍历非递归

  1. class Solution {
  2. public:
  3.     vector<int> inorderTraversal(TreeNode* root) {
  4.         vector<int> ans;
  5.         if(root == nullptr){
  6.             return ans;
  7.         }
  8.         stack<TreeNode* > stk;
  9.         while(!stk.empty() || root != nullptr){
  10.             while(root){
  11.                 stk.push(root);
  12.                 root = root->left;
  13.             }
  14.             ans.push_back(stk.top()->val);
  15.             root = stk.top();
  16.             stk.pop();
  17.             root = root->right;
  18.         }
  19.         return ans;
  20.     }
  21. };

145-3.前序遍历非递归

  1. class Solution {
  2. public:
  3.     vector<int> preorderTraversal(TreeNode* root) {
  4.         if(root == nullptr) return {};
  5.         stack<TreeNode* > stk;
  6.         vector<int> ans;
  7.         while(!stk.empty() || root != nullptr){
  8.             while(root != nullptr){
  9.                 stk.push(root);
  10.                 ans.push_back(stk.top()->val);
  11.                 root = root->left;
  12.             }
  13.             root = stk.top();
  14.             stk.pop();
  15.             root = root->right;
  16.         }
  17.         return ans;
  18.     }
  19. };

230. 二叉搜索树中第K小的元素

这里写的是非递归的迭代解法

难度中等368
给定一个二叉搜索树的根节点 root ，和一个整数 k ，请你设计一个算法查找其中第 k 个最小元素（从 1 开始计数）。

示例 1：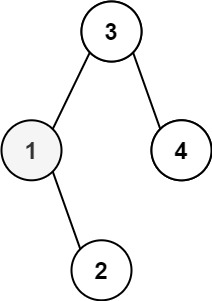
树-遍历 - 图1
输入：root = [3,1,4,null,2], k = 1
输出：1

示例 2：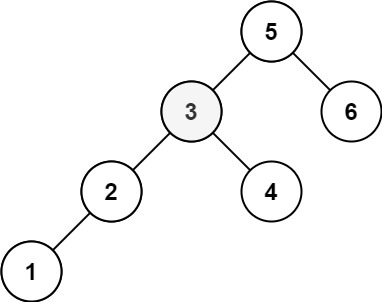
树-遍历 - 图2
输入：root = [5,3,6,2,4,null,null,1], k = 3
输出：3



提示：

  • 树中的节点数为 n 。
  • 1 <= k <= n <= 104

  • 0 <= Node.val <= 104


    进阶：如果二叉搜索树经常被修改（插入/删除操作）并且你需要频繁地查找第 k 小的值，你将如何优化算法？

    1. class Solution {
    2. public:
    3.   int kthSmallest(TreeNode* root, int k) {
    4.       vector<int> ans;
    5.       stack<TreeNode* > stk;
    6.       TreeNode* cur = root;
    7.       while(!stk.empty() || cur){
    8.           //左边先尽量入
    9.           while(cur){
    10.               stk.push(cur);
    11.               cur = cur->left;
    12.           }
    13.           cur = stk.top();
    14.           stk.pop();
    15.           ans.push_back(cur->val);
    16.           cur = cur->right;
    17.       }
    18.       return ans[k - 1];
    19.   }
    20. };

    235. 二叉搜索树的最近公共祖先

    利用BST的特性，只要找满足根结点实在两个目标结点的中间即可

难度简单555
给定一个二叉搜索树, 找到该树中两个指定节点的最近公共祖先。
百度百科中最近公共祖先的定义为：“对于有根树 T 的两个结点 p、q，最近公共祖先表示为一个结点 x，满足 x 是 p、q 的祖先且 x 的深度尽可能大（一个节点也可以是它自己的祖先）。”
例如，给定如下二叉搜索树: root = [6,2,8,0,4,7,9,null,null,3,5]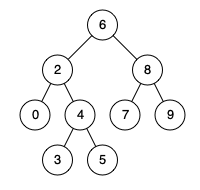
树-遍历 - 图3

示例 1:
输入: root = [6,2,8,0,4,7,9,null,null,3,5], p = 2, q = 8
输出: 6
解释: 节点 2和节点 8的最近公共祖先是 6。
示例 2:
输入: root = [6,2,8,0,4,7,9,null,null,3,5], p = 2, q = 4
输出: 2
解释: 节点 2 和节点 4 的最近公共祖先是 2, 因为根据定义最近公共祖先节点可以为节点本身。

说明:

  • 所有节点的值都是唯一的。
  • p、q 为不同节点且均存在于给定的二叉搜索树中。
    1. class Solution {
    2. public:
    3.   TreeNode* lowestCommonAncestor(TreeNode* root, TreeNode* p, TreeNode* q) {
    4.       while(root){
    5.           if(root->val > p->val && root->val > q->val){
    6.               root = root->left;
    7.           }else if(root->val < p->val && root->val < q->val){
    8.               root = root->right;
    9.           }else{
    10.               break;
    11.           }
    12.       }
    13.       return root;
    14.   }
    15. };

    236. 二叉树的最近公共祖先

    少了搜索树的特点，但其实还是可以用类似的想法，做好递归。从根部开始，本身的函数功能就是根据两个目标结点，找到祖先点然后返回，递归也就要抓住这点。

难度中等1017
给定一个二叉树, 找到该树中两个指定节点的最近公共祖先。
百度百科中最近公共祖先的定义为：“对于有根树 T 的两个节点 p、q，最近公共祖先表示为一个节点 x，满足 x 是 p、q 的祖先且 x 的深度尽可能大（一个节点也可以是它自己的祖先）。”

示例 1：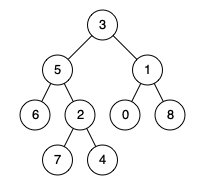
树-遍历 - 图4
输入：root = [3,5,1,6,2,0,8,null,null,7,4], p = 5, q = 1
输出：3
解释：节点 5和节点 1的最近公共祖先是节点 3 。
示例 2：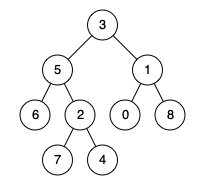
树-遍历 - 图5
输入：root = [3,5,1,6,2,0,8,null,null,7,4], p = 5, q = 4
输出：5
解释：节点 5和节点 4的最近公共祖先是节点 5 。因为根据定义最近公共祖先节点可以为节点本身。

示例 3：
输入：root = [1,2], p = 1, q = 2
输出：1


提示：

  • 树中节点数目在范围 [2, 105] 内。
  • -109 <= Node.val <= 109
  • 所有 Node.val 互不相同 。
  • p != q
  • p 和 q 均存在于给定的二叉树中。
    1. class Solution {
    2. public:
    3.   TreeNode* lowestCommonAncestor(TreeNode* root, TreeNode* p, TreeNode* q) {
    4.       //两种终止条件
    5.       if(root == nullptr) return nullptr;
    6.       //如果遍历到p 和 q那么也终止，说明找到p或者q了
    7.       //这是利用了公共祖先本身允许 祖先是自己
    8.       if(root == p || root == q){
    9.           return root;
    10.       }
    11.       TreeNode* left = lowestCommonAncestor(root->left, p, q);
    12.       TreeNode* right = lowestCommonAncestor(root->right, p, q);
    13.       //对于左右子树分别判断
    14.       //1.如果左右子树中都不包含p或q 那么就返回空
    15.       if(left == nullptr && right == nullptr) return nullptr;
    16.       //2. 3.如果左右子树任意一个为空 那么返回另一边的子数寻找
    17.       if(left == nullptr) return right;
    18.       if(right == nullptr) return left;
    19.       //4.都找到了，那么满足条件，直接返回root 即最近公共祖先
    20.       return root;
    21.   }
    22. };

    剑指 Offer 26. 树的子结构

    难度中等248
    输入两棵二叉树A和B，判断B是不是A的子结构。(约定空树不是任意一个树的子结构)
    B是A的子结构， 即 A中有出现和B相同的结构和节点值。
    例如:
    给定的树 A:
    3<br /> / \<br /> 4 5<br /> / \<br /> 1 2
    给定的树 B：
    4 <br /> /<br /> 1
    返回 true，因为 B 与 A 的一个子树拥有相同的结构和节点值。
    示例 1：
    输入：A = [1,2,3], B = [3,1]
    输出：false

示例 2：
输入：A = [3,4,5,1,2], B = [4,1]
输出：true
限制：
0 <= 节点个数 <= 10000

  1. class Solution {
  2. public:
  3.     //进行当前结构下的匹配
  4.     bool helper(TreeNode* A, TreeNode* B){
  5.         //因为B是A的子结构，所以A的结构应该要>=B，所以不应当先出现A为空的情况
  6.         if(B == nullptr) return true;
  7.         if(A == nullptr) return false;
  8.         //注意这里是值相等，不能用节点等
  9.         if(A->val == B->val) return helper(A->left, B->left) && helper(A->right, B->right);
  10.         return false;
  11.     }
  12.     //找第一个匹配点
  13.     bool isSubStructure(TreeNode* A, TreeNode* B) {
  14.         if(A == nullptr || B == nullptr){
  15.             return false;
  16.         }
  17.         //这必须要把判定子树的过程写到分支中
  18.         //不然如果有重复的节点值时，会直接返回false，可能会错过子结构
  19.         if(A->val == B->val && helper(A->left, B->left) && helper(A->right, B->right)){
  20.             return true;
  21.         }
  22.         return isSubStructure(A->left, B) || isSubStructure(A->right, B);
  23.     }
  24. };

剑指 Offer II 049. 从根节点到叶节点的路径数字之和

先序遍历