介绍
术语
注意📢 结点而不是节点。
节点:被认为是一个实体,有处理能力,如网络中的一台计算机 结点:交叉点、标记,一般算法中的点都称结点。
head、curr、prev、next、temp、tail
对比🆚 首元结点、头结点、头指针
首元结点:第一个含数据域的结点 头结点:在首元结点之前附设的结点,数据域可以不存数据或存链表附加信息如长度等 头指针:指向链表第一个结点(有头结点则指向头结点;没有则指向首元结点)的指针
Tips🤞 dummyNode,哑结点即头结点
设置头结点有什么优点呢?
1、增加了头结点后,首元结点的地址保存在头结点(就是所说的“前驱”结点)的指针域中,则对链表的第一个数据元素的操作与其他数据元素相同,无需进行特殊处理
2、便于空表的和非空表的统一处理;当链表不设头结点时,假设L为单链表的头指针,它应该指向首元结点,则当单链表为长度n为0的空表时,L指针为空(判断空表的条件可记为:L==NULL)
双指针:快慢指针
思考🤔 双指针可以解决哪些问题?进一步思考双指针是否属于滑动窗口?
TopK问题(第K大/小值,倒数第K大/小值)
只有一个后继节点,线性连接,与树/图的核心区别
优点
节点不连续,添加删除灵活,理论上无限扩容
对比
与数组对比
与树对比
思考🤔 如何将数据与结构分离?哪部分是必须的?哪些是可选的?
具体是指数据类型与链表结构的分离,即数据可以int/double也可以是strcut/class/dict等,此时需要类型特定函数,如值比较、复制等
组成
结点:数据域 + 指针域
可选:头结点(相当于管理器,附加链表的额外信息)
管理器在链表的每一个操作中都需更新,具体变化对应管理器中的某项控制类型,如长度,则在删除、添加的同时保持一致
跟数据库操作类似,一般涉及创建、销毁、增(添加)、删(移除)、改(先查再改)、查(遍历)、获取属性(长度、内存空间、是否为空等)
时刻分析每个操作的时间、空间复杂度
创建/构造 通用©
主要是为了分配内存,初始化成员变量
销毁/析构 通用©
主要是为了释放内存,指针变NULL等
注:从内存池中分配的内存,销毁时一般不会需要用户手工释放,但是需要在销毁时将内存归还给内存池
添加元素 通用©
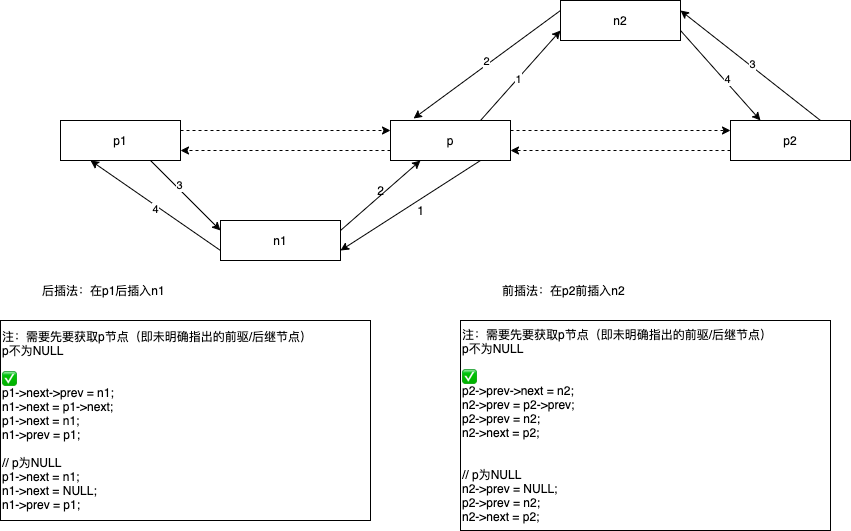
具体场景具体分析,对链表来说,一般分为前插法(头插法)、后插法(尾插法)。
实际应用中一般主要是头插法(不管链表是否有序)、前插法(有序链表中中间插入)
思路
需要知道插入点的前驱、后继节点(指针)
- 先建立连接,再删除连接(一个新的连接会自动断开某个旧的连接,一般无需特意操作);
- 先和不稳定节点(next/prev节点)建立连接,再与稳定节点建立连接,删除无效连接(可能自动删除),举例子:
TODO□ 看图去仔细思考在单双链表中前插法、后插法的底层相似规律
图分析
单向链表
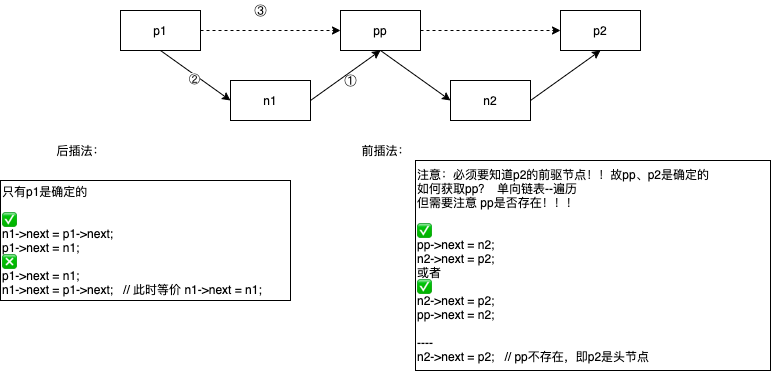
- 必须先要知道前驱节点
双向链表
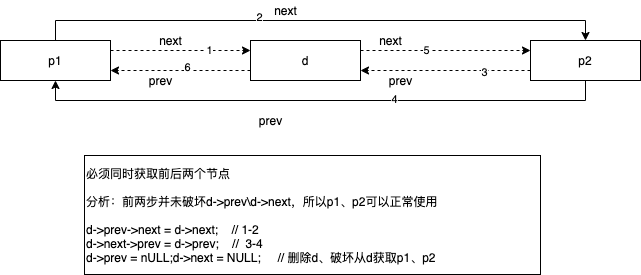
删除节点
单向链表
规律 一般一些小技巧、tips等会有限制,即只有一些特定场合适用,不是通用。
或者说通用的技巧会直接替换原有的旧设计。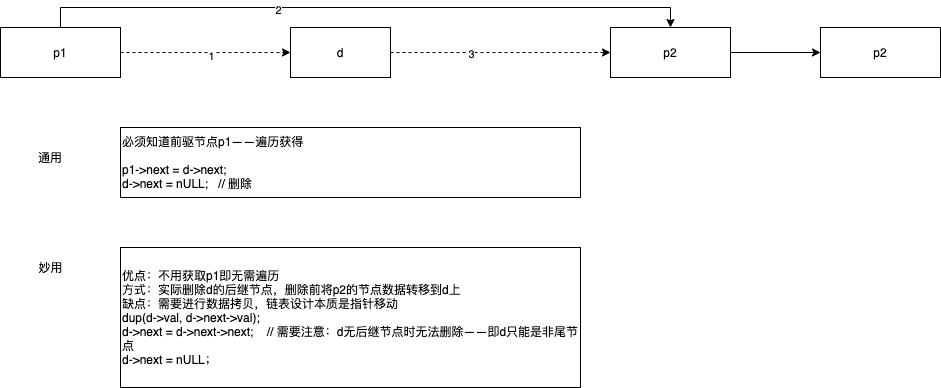
1. 需要知道prev节点(常用)
prev->next = curr->next;
2. 替换下一节点并删除(妙用)
步骤
- 当前节点的数据替换成下一节点的数据
- 删除下一节点
curr->val = curr->next->val;
curr->next = curr->next->next;
双向链表
遍历结点
依据:判断next/prev是否为空,为空则结束(环性链表另外考虑)
查找/修改结点(遍历)
获取长度
当特意为链表添加一个类似管理器的头结点,会明显改善链表性能,且在实际场景中该头结点在存在大量数据结点的链表中所占内存大小可以忽略不计——空间换时间
是否为空
- 长度是否为0,实际应用更通用
head->next == NULL,在算法中更常用(单向链表)
实现
多语言实现(C、C++、Python、Go)
如何充分结合不同语言的特性去进行切合设计
C++ STL中的list实现
Nginx中的ngx_list_t实现
Redis中的list实现
对比 知名开源项目中的链表实现有什么区别和联系
Linux内核中的链表实现应用
链表和数组是所有数据结构的基石,不仅是一种逻辑结构,更在于分别代表了两种不同的存储结构(连续、不连续)
思考在哪些经典场景中用到了链表,比如Linux内核中哪些位置用到了链表,epoll中就绪链表
ringbuf缓存
基于链表实现的跳表
基于有序链表的定时器算法
以下题目中好多方法是通用的,如空间换时间、递归、迭代等解决方式
能用递归的一定可以使用迭代
算法 思维的拓展和延续,思考出不同的解决方案并思考其空间和时间复杂度
思考🤔 下面的算法有实际应用场景吗?
思考🤔 如何将思路想法转换成行动代码,在链表中具体分析需要几个指针变量来表示
- 如何循环
- 循环结束条件是什么
1. 判断是否有环
思考:为什么会快慢指针相遇
类似跑道,速度快的必然会超过速度慢,思考是否可能完美错过,指针是一格一格移动的?如何用数学思维思考
证明 快慢指针一定会相遇
递归法
- 当slow指针到达环结点时,此时fast在环中某个结点(不要去纠结fast已经转了几圈)
- 因为fast速度快,假设fast与slow距离n个结点,则问题可描述成fast还需要n步追上slow
- 假设fast在slow后1个结点,则下一步就相交
- 假设fast在slow后2个结点,则下一步后还差1个结点,再继续执行第3步
- 假设fast在slow后n个结点,则下一步后还差n-1个节点,继续递归到仅差1步后执行第3步
通过上述证明,也可得出在slow跑完整个环之前一定和fast相交——因为n最大为环长度-1
https://blog.csdn.net/jnxxhzz/article/details/82773112
如何判断环?
直观上看,循环过程中结点相同即指针相同,所以常规方案:双循环array、哈希表map/set
- 遍历并与之前比较 O(n^2) 空间 O(1)
- 哈希表 空间复杂O(n)
- 快慢指针
代码实现
1.2 获取环结点(环入口结点)
3. 判断两个链表是否相交
相交——结点指针相同
方案1:双循环
链表A中的每个结点与链表B中的每个结点进行比较
时间复杂度: 空间复杂度:
方案2:哈希表(map/set)——用空间换时间
时间复杂度: 空间复杂度:
方案3:前提,两个链表均有序,再用双指针
和方案一性质相同,但省略掉多余判断
4. 两两交换链表中的结点(1-2-3-4交换后是2-1-4-3)
方案1:用数组存储链表后再重新拼接链表
时间复杂度: 空间复杂度:
方案2:双指针(curr,next)
实际上只需要遍历n/2次即可
时间复杂度: 空间复杂度:
#思考 思路/方案看着简单,但是写代码确如此艰难!
https://leetcode-cn.com/problems/swap-nodes-in-pairs/
5. 合并双链表
5.1 链表求和
6. 反转链表
实际应用场景基本没有,最多反转头尾节点
注:单链表、无环
本质:将节点的next变为prev指针
方法一:遍历(相当于双指针prev、move)
从head->next开始,此时prev=head
while(move){
curr = move;
curr->next = prev;
move = move->next;
}
空间:O(1)
时间:O(n)
方法二:借助map/array 空间换时间
先遍历保存所有节点,再反向遍历新建链表
空间:O(n)
时间:O(2n)
方法三:遍历+头插法
新建链表,遍历源链表,头插
空间:O(n)
时间:O(n)
方法四:递归
思考🤔 为什么可以用递归的思想?哪些情况可以使用递归?实际上链表这个结构非常符合递归思想,如用一串数据创建一个链表?
思考🤔 递归如何去实现
有两种递归???
一种是从大问题到小问题;一种是从小问题到大问题, 如下:
反转链表——从大到小(内部递归)
n阶——从小到大(外部递归)
重要思想:学会假设子结果已正确得到;递归结束条件;用一部分子结果和一个子问题合并成一个更大的子结果
node * reverseList(p) {
if head->next == null
return head
new = reverseList(p->next);
p->next->next = p;
p->next = null;
return new;
}
7. 删除中间结点
通用:需要知道当前结点指针curr、前驱节点指针prev
技巧:在仅知道curr且无途径获取prev时,直接用curr来代替next,再删除next
https://www.jianshu.com/p/d675288f0b81
8. 删除排序链表中重复元素
分两种结果:一种是还保留一个重复结点;一种是不保留任意重复结点
#问题 思路必须更加清晰一些,不要仅晓得大概,不然无法真正将思路转换成代码,会感觉写代码非常吃力
https://leetcode-cn.com/problems/remove-duplicates-from-sorted-list-ii/