思考
- 产生背景即为什么要设计出红黑树?
- 设计妙处在哪?思考自己怎样想到?
- 事物的本质是什么?是数据结构,那么有哪些数据结构通用性质?
- 接第3问,如何定义红黑树,有哪些操作,复杂度是怎样的?哪些是API,哪些是内部操作?
- 优缺点是什么?适用哪些场景?现已应用在哪些场景?
背景
AVL插入删除需要复杂操作来维持平衡性——降低平衡性来提高插入删除效率
定义
- 基于二叉排序树(二叉查找树)
中序:顺序
快速查找- 自平衡
在进行插入和删除等可能会破坏树的平衡的操作时,需要重新自处理达到平衡状态
- 自平衡
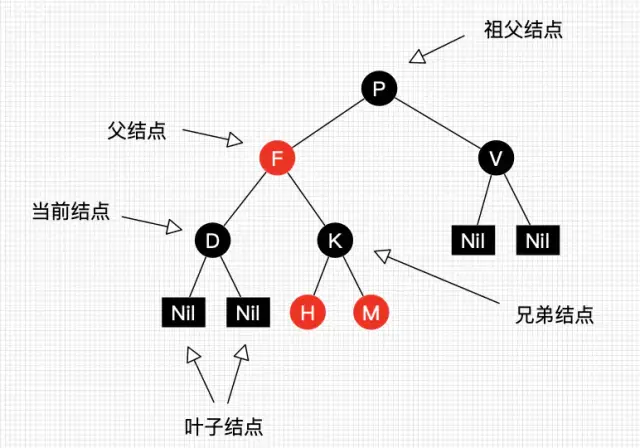
特性
- 节点只有红黑2色
- 根节点是黑色
- 叶子节点都是空的黑色节点——即NIL节点
- 红色节点无法相邻,即不能是父子关系
- 每个节点到叶子节点的路径上黑色节点数量相同
操作
30张图带你彻底理解红黑树
红黑树(一)之 原理和算法详细介绍 - 如果天空不死 - 博客园 (cnblogs.com)
红黑树(二)之 C语言的实现 - 如果天空不死 - 博客园这篇详细介绍了插入、删除情景,花时间去进行学习整理
先尝试 recolor,如果 recolor 不能达到红黑树的 4 点要求,然后我们尝试 rotation
插入、删除、修改都必须先查询,查询:$O(logn)$ == $O(h)$,n为结点总数,h为高度。且查询次数相对稳定
- 自平衡
- recolor (重新标记黑色或红色——变色)
- rotation (旋转,这是树达到平衡的关键)
- 左旋
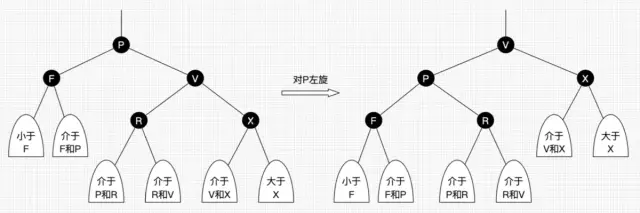
以某个结点作为支点(旋转结点),其右子结点变为旋转结点的父结点,右子结点的左子结点变为旋转结点的右子结点,左子结点保持不变 - 右旋
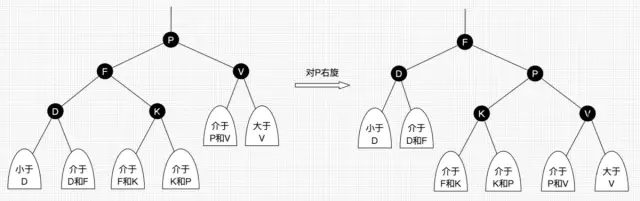
以某个结点作为支点(旋转结点),其左子结点变为旋转结点的父结点,左子结点的右子结点变为旋转结点的左子结点,右子结点保持不变查询
步骤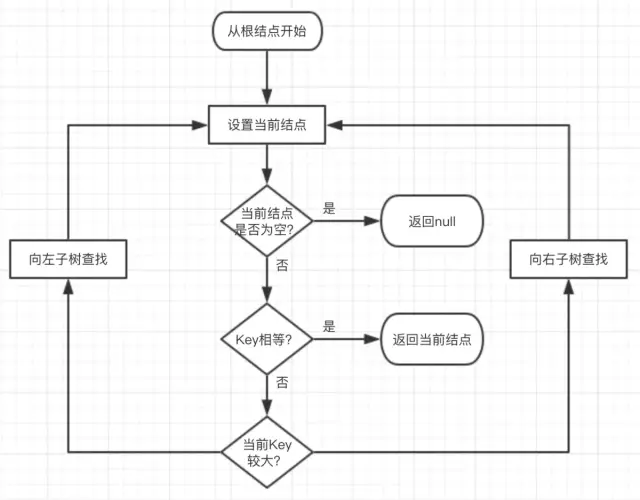
从根结点开始查找,把根结点设置为当前结点;
若当前结点为空,返回null;
若当前结点不为空,用当前结点的key跟查找key作比较;
若当前结点key等于查找key,那么该key就是查找目标,返回当前结点;
若当前结点key大于查找key,把当前结点的左子结点设置为当前结点,重复步骤2;
若当前结点key小于查找key,把当前结点的右子结点设置为当前结点,重复步骤2;
- 左旋
- 时间复杂度- O(logN)- 最坏时间复杂度为O(2lgN)即整颗树刚好红黑相隔的时候
插入
按照规则,插入的节点只能是叶子节点且为红色。
一查找插入的位置;二插入后自平衡
插入的节点总是红色,因为:若为黑色,插入节点子树平衡必被破坏
所有插入操作都是在叶子结点进行的
- 步骤从根结点开始查找;若根结点为空,那么插入结点作为根结点,结束。若根结点不为空,那么把根结点作为当前结点;若当前结点为null,返回当前结点的父结点,结束。若当前结点key等于查找key,那么该key所在结点就是插入结点,更新结点的值,结束。若当前结点key大于查找key,把当前结点的左子结点设置为当前结点,重复步骤4;若当前结点key小于查找key,把当前结点的右子结点设置为当前结点,重复步骤4;
删除
修改
应用
epoll
Linux虚拟内存管理
关联数组,如STL的set、map
定时器
Nginx
- 红黑树,超强动静图详解,简单易懂 - 知乎 (zhihu.com)
- 如何查看前驱后继节点
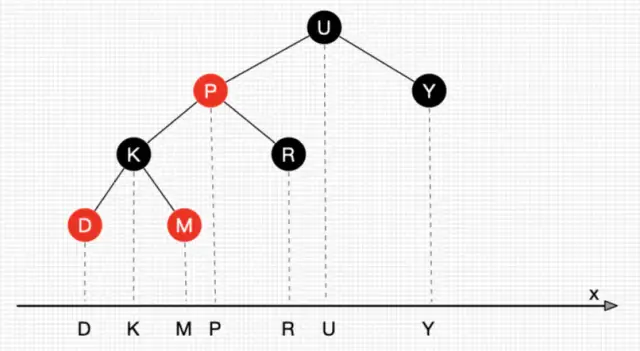
把二叉树所有结点投射在X轴上,所有结点都是从左到右排好序的,所有目标结点的前后结点就是对应前继和后继结点