原文地址：https://blog.csdn.net/guorui_java/article/details/106341658
查找算法分类：
1、静态查找和动态查找
2、无序查找和有序查找

一、二分查找

1.1 基本思想

也称为折半查找，属于有序查找算法。用给定值value先与中间结点的关键字比较，中间结点把线形表分成两个子表，若相等，则查找成功；若不相等，再根据K与该中间结点关键字的比较结果确定下一步查找哪个子表，这样递归进行，直到查找到或查找结束发现表中没有这样的结点。

1.2 复杂度分析

最坏情况下，关键字比较次数为log2(n+1)，且期望时间复杂度O(log2n)；

1.3 大话数据结构

二分查找的前提条件是需要有序表顺序存储，对于静态查找表，一次排序后不再变化，二分查找能得到不错的效率。但对于需要频繁执行插入或删除操作的数据集来说，维护有序的排序会带来不小的工作量，此时不建议使用二分查找。

1.4 代码实例

  1. public static List<Integer> binarySearch2(int[] arr, int left, int right, int findVal){
  2.     // 当 left > right 时，说明递归整个数组，但是没有找到
  3.     if (left > right) {
  4.         return new ArrayList<Integer>();
  5.     }
  7.     int mid = (left + right) / 2;
  8.     int midVal = arr[mid];
  10.     if (findVal > midVal) { // 向 右递归
  11.         return binarySearch2(arr, mid + 1, right, findVal);
  12.     } else if (findVal < midVal) { // 向左递归
  13.         return binarySearch2(arr, left, mid - 1, findVal);
  14.     } else {
  15.         List<Integer> resIndexlist = new ArrayList<Integer>();
  16.         //向mid 索引值的左边扫描，将所有满足 1000， 的元素的下标，加入到集合ArrayList
  17.         int temp = mid - 1;
  18.         while (true){
  19.             if(temp < 0 || arr[temp] != findVal){
  20.                 break;
  21.             }
  22.             resIndexlist.add(temp);
  23.             temp--;
  24.         }
  25.         resIndexlist.add(mid);
  26.         //向mid 索引值的右边扫描，将所有满足 1000， 的元素的下标，加入到集合ArrayList
  27.         temp = mid + 1;
  28.         while (true){
  29.             if(temp > arr.length - 1 || arr[temp] != findVal){
  30.                 break;
  31.             }
  32.             resIndexlist.add(temp);
  33.             temp++;
  34.         }
  35.         return resIndexlist;
  36.     }
  37. }

二、插值查找

2.1 基本思想

基于二分查找算法，将查找点的选择改进为自适应选择，可以提升查找算法的平均性能比折半查找要好的多。
如果数组中分布不均匀，那么插值查找未必是很合适的选择。

2.2 mid变量的计算

在二分查找中：
mid=(left+right)/2；
在插值查找中：
mid=left + (right - left)*(findVal - arr[left])/(arr[right]-arr[left])；
这个公式很牛！

2.3 代码实例

  1. public static int insertValueSearch(int[] arr, int left, int right, int findVal){
  2.     if(left>right || findVal<arr[left] || findVal>arr[right]){
  3.         return -1;
  4.     }
  6.     int mid = left + (right - left)*(findVal - arr[left])/(arr[right]-arr[left]);
  7.     int midVal = arr[mid];
  8.     if(findVal>midVal){
  9.         return insertValueSearch(arr,mid + 1,right,findVal);
  10.     }else if(findVal>midVal){
  11.         return insertValueSearch(arr,left,mid - 1,findVal);
  12.     }else {
  13.         return mid;
  14.     }
  15. }

2.4 插值查找算法和二分查找算法对比

（1）对于数据量较大，数值分布比较均匀的数组来说，使用插值查找算法，速度更快一些；
（2）但是对于数值分布不均匀的数组来说，建议使用二分查找算法；

三、斐波那契查找算法

3.1 基本思想

斐波那契数列又称黄金分割数列，黄金分割点，0.618。
{1,1,2,3,5,8,13,21,55}，发现规律了吗，前一个数值除以后一个数值，无限接近0.618，这个数列就称为斐波那契数列。

3.2 mid值的计算

斐波那契查找算法和二分查找差不多，但斐波那契没有递归，只是换一种方法寻找mid值，
mid=left + fibonacciArr[f-1] -1;
fibonacciArr：表示斐波那契数组；
f：表示斐波那契数列的第f个元素；
fibonacciArr[f] = fibonacciArr[f-1] + fibonacciArr[f-2];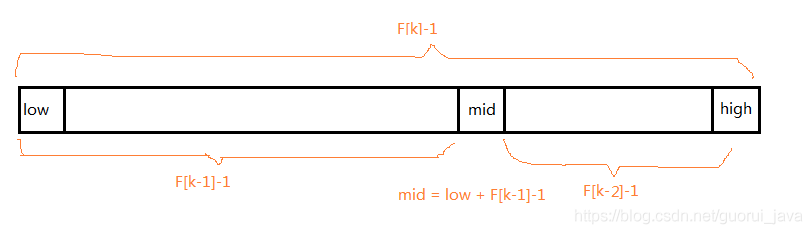
10.二分查找、插值查找、斐波那契查找 - 图1

3.3 代码实现

  1. //因为后面我们mid=low+F(k-1)-1，需要使用到斐波那契数列，因此我们需要先获取到一个斐波那契数列
  2. //非递归方法得到一个斐波那契数列
  3. public static int[] fibonacci(){
  4.     int[] fibonacci = new int[20];
  5.     fibonacci[0] = 1;
  6.     fibonacci[1] = 1;
  7.     for (int i = 2; i < fibonacci.length - 1; i++) {
  8.         fibonacci[i] = fibonacci[i-1] + fibonacci[i-2];
  9.     }
  10.     return fibonacci;
  11. }
  13. //编写斐波那契查找算法
  14. //使用非递归的方式编写算法
  15. public static int fibonacciSearch(int[] arr,int findVal){
  16.     int left = 0;
  17.     int right = arr.length - 1;
  18.     int f = 0;//表示斐波那契分割数值的下标
  19.     int mid = 0;
  20.     int[] fibonacci = fibonacci();
  21.     //获取到斐波那契分割数值的下标
  22.     while (right > fibonacci[f] - 1){
  23.         f++;
  24.     }
  26.     //因为 f[f] 值 可能大于 arr 的 长度，因此我们需要使用Arrays类，构造一个新的数组，并指向temp[]
  27.     //不足的部分会使用0填充
  28.     int[] temp = Arrays.copyOf(arr,fibonacci[f]);
  29.     //实际上需求使用arr数组最后的数填充 temp
  30.     //举例:
  31.     //temp = {1,8, 10, 89, 1000, 1234, 0, 0}  => {1,8, 10, 89, 1000, 1234, 1234, 1234,}
  32.     for (int i = right + 1; i < temp.length; i++) {
  33.         temp[i] = arr[right];
  34.     }
  36.     // 使用while来循环处理，找到我们的数 findVal
  37.     while (left <= right) {
  38.         //fibonacci寻找mid固定写法
  39.         mid = left + fibonacci[f - 1] - 1;
  40.         if (findVal < temp[mid]) { //我们应该继续向数组的前面查找(左边)
  41.             right = mid - 1;
  42.             //为甚是 f--
  43.             //说明
  44.             //1. 全部元素 = 前面的元素 + 后边元素
  45.             //2. fibonacci[f] = fibonacci[f-1] + fibonacci[f-2]
  46.             //因为 前面有 fibonacci[f-1]个元素,所以可以继续拆分 fibonacci[f-1] = fibonacci[f-2] + fibonacci[f-3]
  47.             //即 在 fibonacci[f-1] 的前面继续查找 f--
  48.             //即下次循环 mid = fibonacci[f-1-1]-1
  49.             f--;
  50.         } else if (findVal > temp[mid]) { // 我们应该继续向数组的后面查找(右边)
  51.             left = mid + 1;
  52.             //为什么是f -=2
  53.             //说明
  54.             //1. 全部元素 = 前面的元素 + 后边元素
  55.             //2. fibonacci[f] = fibonacci[f-1] + fibonacci[f-2]
  56.             //3. 因为后面我们有f[f-2] 所以可以继续拆分 fibonacci[f-2] = fibonacci[f-3] + fibonacci[f-4]
  57.             //4. 即在fibonacci[f-2] 的前面进行查找 f -=2
  58.             //5. 即下次循环 mid = fibonacci[f - 1 - 2] - 1
  59.             f -= 2;
  60.         }else { //找到
  61.             //需要确定，返回的是哪个下标
  62.             if(mid <= right) {
  63.                 return mid;
  64.             } else {
  65.                 return right;
  66.             }
  67.         }
  68.     }
  69.     return -1;
  70. }

3.4 斐波那契查找算法与二分查找算法对比

斐波那契的性能对比优于二分查找，实验数据表明，斐波那契查找算法大约较二分查找算法快17%，但是这个归功于一个原因，斐波那契查找算法在分割时只有加、减运算，而没有乘法运算。