原文地址：https://blog.csdn.net/guorui_java/article/details/106270186

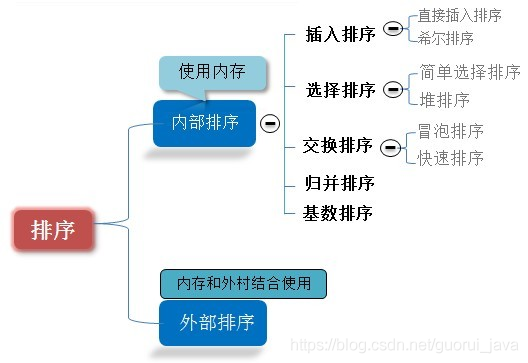
一、算法分类

9.常见的7种排序算法 - 图1

算法的时间复杂度和空间复杂度：
9.常见的7种排序算法 - 图2

二、七大排序算法

（一）冒泡排序

1、基本思想
依次比较相邻的两个数，将比较小的数放在前面，比较大的数放在后面。
2、动态效果图
9.常见的7种排序算法 - 图3
3、代码实现

  1. //冒泡排序
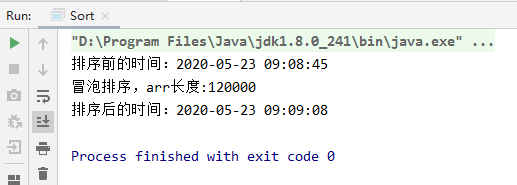
  2. private static void bubbleSort(int[] arr){
  3.     // 标识变量，表示是否进行过交换
  4.     boolean flag = false;
  5.     int temp = 0;
  6.     for (int i = 0; i < arr.length-1; i++) {
  7.         for (int j = 0; j < arr.length-1-i; j++) {
  8.             // 如果前面的数比后面的数大，则交换
  9.             if(arr[j]>arr[j+1]){
  10.                 flag = true;
  11.                 temp = arr[j];
  12.                 arr[j] = arr[j+1];
  13.                 arr[j+1] = temp;
  14.             }
  15.         }
  16.         // 在一趟排序中，一次交换都没有发生过
  17.         if(!flag){
  18.             break;
  19.         }
  20.     }
  21. }

4、速度测试
冒泡排序：120000数据，23秒
9.常见的7种排序算法 - 图4

（二）选择排序

1、基本思想
（1）在序列中找到最小元素，放在第一个位置；
（2）从剩余未排序元素中继续寻找最小元素，放在第二个位置；
以此类推，直到排序完毕。
2、动态效果图
9.常见的7种排序算法 - 图5
3、代码实现

  1. //选择排序
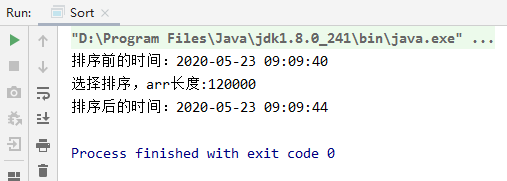
  2. public static void selectSort(int[] arr) {
  3.     for (int i = 0; i < arr.length - 1; i++) {
  4.         int minIndex = i;
  5.         int min = arr[minIndex];
  6.         for(int j  = 1 + i;j<arr.length;j++){
  7.             if(min > arr[j]){
  8.                 min = arr[j];
  9.                 minIndex = j;
  10.             }
  11.         }
  12.         arr[minIndex] = arr[i];
  13.         arr[i] = min;
  14.     }
  15. }

4、速度测试
选择排序：120000数据，4秒
9.常见的7种排序算法 - 图6

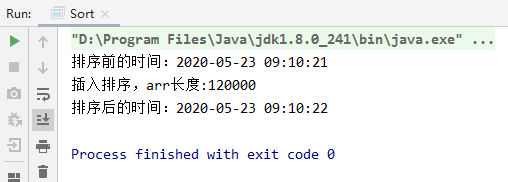
（三）插入排序

1、基本思想
把n个待排序的元素第一位看成有序表，其它的看成无序表，排序过程中，每次从无序表中取出一个数，依次与有序表中的数进行比较，插入到合适的位置。
2、动态效果图
9.常见的7种排序算法 - 图7
3、代码实现

  1. //插入排序
  2. public static void insertSort(int[] arr ){
  3.     int insertVal = 0;
  4.     int insertIndex = 0;
  5.     for (int i = 1; i < arr.length; i++) {
  6.         //定义待插入的数
  7.         insertVal = arr[i];
  8.         // 即arr[i]的前面这个数的下标
  9.         insertIndex = i - 1;
  10.         // 给insertVal 找到插入的位置
  11.         // 说明
  12.         // 1. insertIndex >= 0 保证在给insertVal 找插入位置，不越界
  13.         // 2. insertVal < arr[insertIndex] 待插入的数，还没有找到插入位置
  14.         // 3. 就需要将 arr[insertIndex] 后移
  15.         while(insertIndex >= 0 && insertVal < arr[insertIndex]){
  16.             arr[insertIndex+1] = arr[insertIndex];
  17.             insertIndex--;
  18.         }
  19.         // 当退出while循环时，说明插入的位置找到, insertIndex + 1
  20.         if(insertIndex + 1 != i){
  21.             arr[insertIndex+1] = insertVal;
  22.         }
  23.     }
  24. }

4、速度测试
插入排序：120000数据，1秒
9.常见的7种排序算法 - 图8

（四）希尔排序

1、基本思想
希尔排序也是一种插入排序，它是简单插入排序经过改进之后的一个更高效的版本，也称为缩小增量排序，同时该算法也是冲破O(n²)的第一批算法之一。它与插入排序的不同之处在于，它会优先比较较远的元素。
2、效果图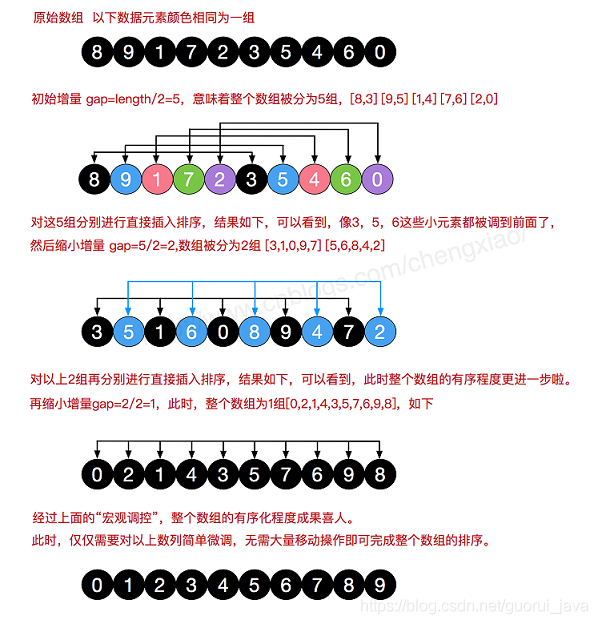
9.常见的7种排序算法 - 图9
3、代码实例
希尔排序有两种方式。
①希尔排序（冒泡排序）

  1. //希尔排序
  2. // 使用逐步推导的方式来编写希尔排序
  3. // 希尔排序时， 对有序序列在插入时采用交换法,
  4. // 思路(算法) ===> 代码
  5. public static void shellSort(int[] arr){
  6.     // 根据前面的逐步分析，使用循环处理
  7.     for(int step = arr.length/2;step>0;step /= 2 ){
  8.         for (int i = step; i < arr.length; i++) {
  9.             // 遍历各组中所有的元素(共step组，每组有个元素), 步长step
  10.             for (int j = i - step; j >= 0; j -= step) {
  11.                 // 如果当前元素大于加上步长后的那个元素，说明交换
  12.                 if (arr[j] > arr[j + step]) {
  13.                     int temp = arr[j];
  14.                     arr[j] = arr[j + step];
  15.                     arr[j + step] = temp;
  16.                 }
  17.             }
  18.         }
  19.     }
  20. }

速度测试：
冒泡法希尔排序：120000数据，11秒
9.常见的7种排序算法 - 图10
②希尔排序（插入排序）

  1. //对交换式的希尔排序进行优化->插入法
  2. public static void shellSort2(int[] arr) {
  3. // 增量step, 并逐步的缩小增量
  4. for (int step = arr.length / 2; step > 0; step /= 2) {
  5.     // 从第step个元素，逐个对其所在的组进行直接插入排序
  6.     for (int i = step; i < arr.length; i++) {
  7.         int j = i;
  8.         int temp = arr[j];
  9.         if(arr[j]<arr[j-step]){
  10.             while (j - step >= 0&&temp<arr[j-step]){
  11.                 arr[j] = arr[j-step];
  12.                 j -= step;
  13.             }
  14.             arr[j] = temp;
  15.         }
  16.     }
  17. }

速度测试：
插入法希尔排序：12000000数据，4秒，叹为观止
9.常见的7种排序算法 - 图11

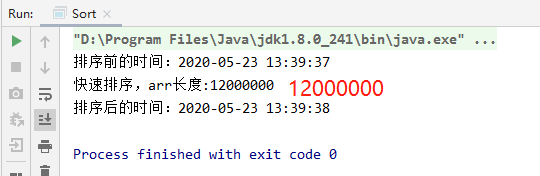
（五）快速排序

1、基本思想
通过一趟排序将待排记录分割成独立的两部分，其中一部分记录的关键字均比另一部分的关键字小，则可分别对这两部分记录进行排序，以达到整个排序的过程。
2、效果图
9.常见的7种排序算法 - 图12
3、算法描述

  • 快速排序使用分治法把一个串分为两个子串；
  • 找一个基准点，暂时选中间点为基准点；
  • 重新排序数列，比基准值小的放在基准点前面，大的放在后面；
  • 递归的把小于基准值的子数列和大于基准值的子数列排序；

4、代码实例

  1. //快速排序
  2. public static void quickSort(int[] arr,int left, int right) {
  3.     int l = left; //左下标
  4.     int r = right; //右下标
  5.     //pivot 中轴值
  6.     int pivot = arr[(left + right) / 2];
  7.     int temp = 0; //临时变量，作为交换时使用
  8.     //while循环的目的是让比pivot 值小放到左边
  9.     //比pivot 值大放到右边
  10.     while( l < r) {
  11.         //在pivot的左边一直找,找到大于等于pivot值,才退出
  12.         while( arr[l] < pivot) {
  13.             l += 1;
  14.         }
  15.         //在pivot的右边一直找,找到小于等于pivot值,才退出
  16.         while(arr[r] > pivot) {
  17.             r -= 1;
  18.         }
  19.         //如果l >= r说明pivot 的左右两的值，已经按照左边全部是
  20.         //小于等于pivot值，右边全部是大于等于pivot值
  21.         if( l >= r) {
  22.             break;
  23.         }
  25.         //交换
  26.         temp = arr[l];
  27.         arr[l] = arr[r];
  28.         arr[r] = temp;
  30.         //如果交换完后，发现这个arr[l] == pivot值 相等 r--， 前移
  31.         if(arr[l] == pivot) {
  32.             r -= 1;
  33.         }
  34.         //如果交换完后，发现这个arr[r] == pivot值 相等 l++， 后移
  35.         if(arr[r] == pivot) {
  36.             l += 1;
  37.         }
  38.     }
  40.     // 如果 l == r, 必须l++, r--, 否则为出现栈溢出
  41.     if (l == r) {
  42.         l += 1;
  43.         r -= 1;
  44.     }
  45.     //向左递归
  46.     if(left < r) {
  47.         quickSort(arr, left, r);
  48.     }
  49.     //向右递归
  50.     if(right > l) {
  51.         quickSort(arr, l, right);
  52.     }
  53. }

5、速度测试
快速排序：12000000数据，1秒，逆天而行
9.常见的7种排序算法 - 图13

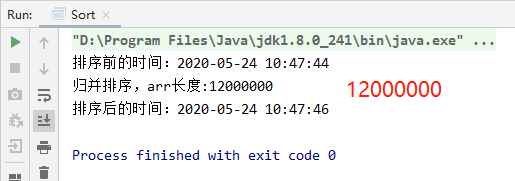
（六）归并排序

1、基本思想
归并排序采用经典的分治策略，分治法将问题分成一些小的问题然后递归解决，则治的阶段就是将分的阶段得到的答案修补在一起，即分而治之。
2、效果图
9.常见的7种排序算法 - 图14

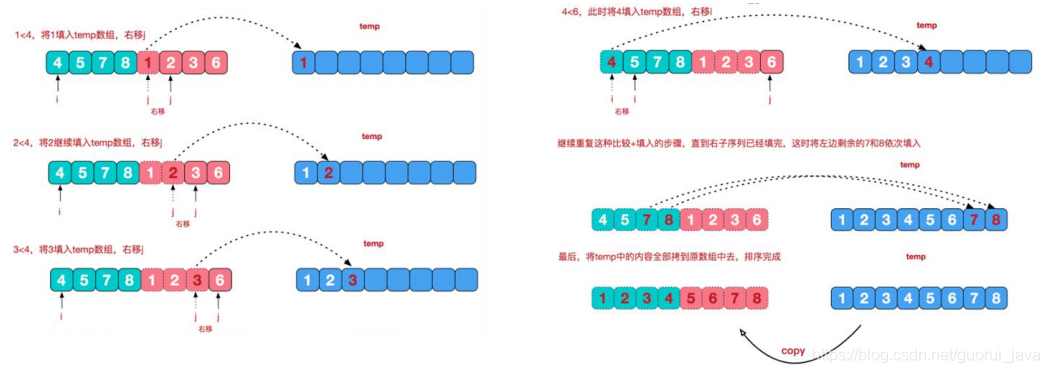
9.常见的7种排序算法 - 图15
3、代码实现

  1. //归并排序
  2. public static void mergerSort(int[] arr,int left,int right,int[] temp){
  3.     if(left<right){
  4.         //中间索引
  5.         int middle = (left + right)/2;
  6.         //向左递归进行分解
  7.         mergerSort(arr,left,middle,temp);
  8.         //向右递归进行分解
  9.         mergerSort(arr,middle + 1,right,temp);
  10.         //合并
  11.         merger(arr, left, middle, right, temp);
  12.     }
  13. }
  15. //合并
  16. public static void merger(int[] arr,int left,int middle,int right,int[] temp){
  17.     int i = left; // 初始化i, 左边有序序列的初始索引
  18.     int j = middle + 1; //初始化j, 右边有序序列的初始索引
  19.     int t = 0; // 指向temp数组的当前索引
  21.     //先把左右两边(有序)的数据按照规则填充到temp数组
  22.     //直到左右两边的有序序列，有一边处理完毕为止
  23.     while (i <= middle && j <= right) {//继续
  24.         //如果左边的有序序列的当前元素，小于等于右边有序序列的当前元素
  25.         //即将左边的当前元素，填充到 temp数组
  26.         //然后 t++, i++
  27.         if(arr[i] <= arr[j]){
  28.             temp[t] = arr[i];
  29.             t++;
  30.             i++;
  31.         }else { //反之,将右边有序序列的当前元素，填充到temp数组
  32.             temp[t] = arr[j];
  33.             t++;
  34.             j++;
  35.         }
  36.     }
  38.     //把有剩余数据的一边的数据依次全部填充到temp
  39.     //左边的有序序列还有剩余的元素，就全部填充到temp
  40.     while (i <= middle){
  41.         temp[t] = arr[i];
  42.         t++;
  43.         i++;
  44.     }
  46.     //右边的有序序列还有剩余的元素，就全部填充到temp
  47.     while (j <= right){
  48.         temp[t] = arr[j];
  49.         t++;
  50.         j++;
  51.     }
  53.     //将temp数组的元素拷贝到arr
  54.     //注意，并不是每次都拷贝所有
  55.     t = 0;
  56.     int tempLeft = left; //
  57.     while (tempLeft <= right){
  58.         arr[tempLeft] = temp[t];
  59.         t++;
  60.         tempLeft++;
  61.     }
  62. }

4、速度测试
归并排序：12000000数据，1秒，惊为天人
9.常见的7种排序算法 - 图16

（七）基数排序

1、基本思想
将所有带比较数值统一为同样的数位长度，数据较短的数前面补0，然后从最低位开始依次进行依次排序，这样从最低位排序一直到最高位排序完成之后，数列就变成了一个有序序列。
2、动态效果图
9.常见的7种排序算法 - 图17
3、代码实例

  1. //基数排序
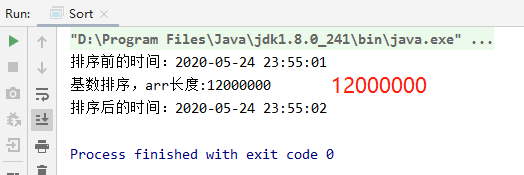
  2. public static void radixSort(int arr[]){
  3.     System.out.println("基数排序，arr长度:"+arr.length);
  4.     //1. 得到数组中最大的数的位数
  5.     int max = arr[0]; //假设第一数就是最大数
  6.     for(int i = 1; i < arr.length; i++) {
  7.         if (arr[i] > max) {
  8.             max = arr[i];
  9.         }
  10.     }
  11.     //得到最大数是几位数
  12.     int maxLength = (max + "").length();
  14.     //定义一个二维数组，表示10个桶, 每个桶就是一个一维数组
  15.     //说明
  16.     //1. 二维数组包含10个一维数组
  17.     //2. 为了防止在放入数的时候，数据溢出，则每个一维数组(桶)，大小定为arr.length
  18.     //3. 名明确，基数排序是使用空间换时间的经典算法
  19.     int[][] bucket = new int[10][arr.length];
  21.     //为了记录每个桶中，实际存放了多少个数据,我们定义一个一维数组来记录各个桶的每次放入的数据个数
  22.     //可以这里理解
  23.     //比如：bucketElementCounts[0] , 记录的就是  bucket[0] 桶的放入数据个数
  24.     int[] bucketElementCounts = new int[10];
  26.     //这里我们使用循环将代码处理
  27.     for(int i = 0 , n = 1; i < maxLength; i++, n *= 10) {
  28.         //(针对每个元素的对应位进行排序处理)， 第一次是个位，第二次是十位，第三次是百位..
  29.         for(int j = 0; j < arr.length; j++) {
  30.             //取出每个元素的对应位的值
  31.             int digitOfElement = arr[j] / n % 10;
  32.             //放入到对应的桶中
  33.             bucket[digitOfElement][bucketElementCounts[digitOfElement]] = arr[j];
  34.             bucketElementCounts[digitOfElement]++;
  35.         }
  36.         //按照这个桶的顺序(一维数组的下标依次取出数据，放入原来数组)
  37.         int index = 0;
  38.         //遍历每一桶，并将桶中是数据，放入到原数组
  39.         for(int k = 0; k < bucketElementCounts.length; k++) {
  40.             //如果桶中，有数据，我们才放入到原数组
  41.             if(bucketElementCounts[k] != 0) {
  42.                 //循环该桶即第k个桶(即第k个一维数组), 放入
  43.                 for(int l = 0; l < bucketElementCounts[k]; l++) {
  44.                     //取出元素放入到arr
  45.                     arr[index++] = bucket[k][l];
  46.                 }
  47.             }
  48.             //第i+1轮处理后，需要将每个 bucketElementCounts[k] = 0 ！！！！
  49.             bucketElementCounts[k] = 0;
  51.         }
  52.     }
  53. }

4、速度测试
基数排序：12000000数据，1秒，速度感人
9.常见的7种排序算法 - 图18