原文地址：https://blog.csdn.net/guorui_java/article/details/106398737
组的搜索比较方便，可以直接用下标，但删除和插入就比较麻烦；
链表与之相反，删除和插入元素很快，但查找比较慢；
此时，二叉树应运而生，二叉树既有链表的好处，也有数组的好处，在处理大批量的动态数据时比较好用，是一种折中的选择。
文件系统和数据库系统一般都是采用树（特别是B树）的数据结构数据，主要为排序和检索的效率。
二叉树是一种最基本最典型的排序树，用于教学和研究树的特性，本身很少在实际中进行应用，因为缺点太明显，就像冒泡排序一样，因为效率问题并不实用，但也是我们必须会的。

一、二叉树缺点

1、顺序存储可能会浪费空间（在非完全二叉树的时候），但是读取某个指定的结点的时候效率比较高O(0)；
2、链式存储相对于二叉树，浪费空间较少，但是读取某个结点的时候效率偏低O(nlogn)。
11.二叉树 - 图1

二、遍历与结点删除

二叉树是一种非常重要的数据结构，非常多的数据结构都是基于二叉树的基础演变而来的。对于二叉树有深度遍历和广度遍历，深度遍历有前序、中序以及后序三种遍历方法，广度遍历即我们寻常所说的层次遍历。由于树的定义本身就是递归定义，因此采用递归的方法实现树的三种遍历。
对于一段代码来说，可读性有时候要比代码本身的效率要重要的多。

2.1 四种基本的遍历思想

  1. 前序遍历：根结点 -->左子树-->右子树；<br />    中序遍历：左子树 -->根结点-->右子树；<br />    后续遍历：左子树 -->右子树-->根结点；<br />    层次遍历：仅仅需按成次遍历即可；

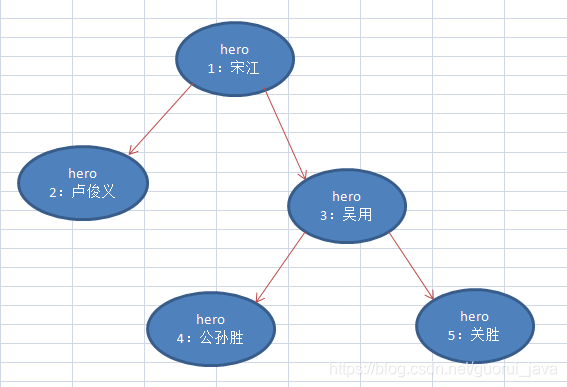
2.2 自定义二叉树

11.二叉树 - 图2

2.3 代码实现

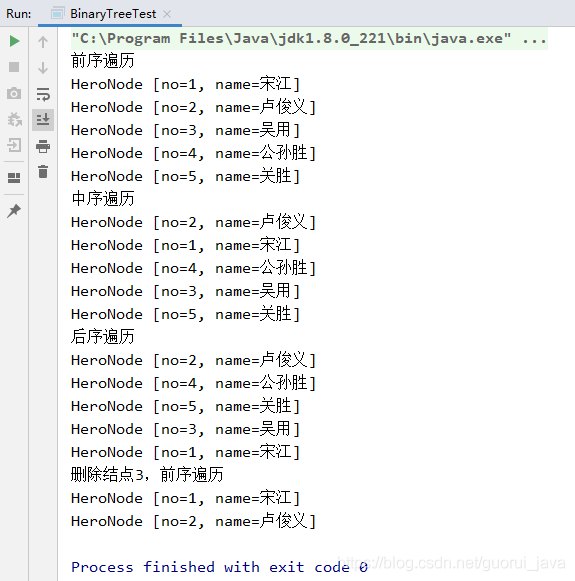
  1. package dataStructure.tree;
  3. public class BinaryTreeTest {
  4.     public static void main(String[] args) {
  5.         //创建一个二叉树
  6.         BinaryTree binaryTree = new BinaryTree();
  7.         //创建结点
  8.         HeroNode root = new HeroNode(1, "宋江");
  9.         HeroNode node2 = new HeroNode(2, "卢俊义");
  10.         HeroNode node3 = new HeroNode(3, "吴用");
  11.         HeroNode node4 = new HeroNode(4, "公孙胜");
  12.         HeroNode node5 = new HeroNode(5, "关胜");
  13.         root.setLeft(node2);
  14.         root.setRight(node3);
  15.         node3.setLeft(node4);
  16.         node3.setRight(node5);
  17.         binaryTree.setRoot(root);
  18.         System.out.println("前序遍历");
  19.         binaryTree.preOrder();
  20.         System.out.println("中序遍历");
  21.         binaryTree.midOrder();
  22.         System.out.println("后序遍历");
  23.         binaryTree.postOrder();
  24.         binaryTree.delNode(3);
  25.         System.out.println("删除结点3，前序遍历");
  26.         binaryTree.preOrder();
  27.     }
  28. }
  30. //定义BinaryTree 二叉树
  31. class BinaryTree {
  32.     private HeroNode root;
  34.     public HeroNode getRoot() {
  35.         return root;
  36.     }
  38.     public void setRoot(HeroNode root) {
  39.         this.root = root;
  40.     }
  41.     //前序遍历
  42.     public void preOrder() {
  43.         if(this.root != null) {
  44.             this.root.preOrder();
  45.         }else {
  46.             System.out.println("二叉树为空，不能遍历");
  47.         }
  48.     }
  49.     //中序遍历
  50.     public void midOrder() {
  51.         if(this.root != null) {
  52.             this.root.midOrder();
  53.         }else {
  54.             System.out.println("二叉树为空，无法遍历");
  55.         }
  56.     }
  57.     //后序遍历
  58.     public void postOrder() {
  59.         if(this.root != null) {
  60.             this.root.postOrder();
  61.         }else {
  62.             System.out.println("二叉树为空，无法遍历");
  63.         }
  64.     }
  66.     //删除结点
  67.     public void delNode(int no) {
  68.         if(root != null) {
  69.             //如果只有一个root结点, 这里立即判断root是不是就是要删除结点
  70.             if(root.getNo() == no) {
  71.                 root = null;
  72.             } else {
  73.                 //递归删除
  74.                 root.delNode(no);
  75.             }
  76.         }else{
  77.             System.out.println("空树，不能删除~");
  78.         }
  79.     }
  80. }
  82. //先创建HeroNode 结点
  83. class HeroNode {
  84.     private int no;
  85.     private String name;
  86.     private HeroNode left; //默认null
  87.     private HeroNode right; //默认null
  88.     public HeroNode(int no, String name) {
  89.         this.no = no;
  90.         this.name = name;
  91.     }
  92.     public int getNo() {
  93.         return no;
  94.     }
  95.     public void setNo(int no) {
  96.         this.no = no;
  97.     }
  98.     public String getName() {
  99.         return name;
  100.     }
  101.     public void setName(String name) {
  102.         this.name = name;
  103.     }
  104.     public HeroNode getLeft() {
  105.         return left;
  106.     }
  107.     public void setLeft(HeroNode left) {
  108.         this.left = left;
  109.     }
  110.     public HeroNode getRight() {
  111.         return right;
  112.     }
  113.     public void setRight(HeroNode right) {
  114.         this.right = right;
  115.     }
  116.     @Override
  117.     public String toString() {
  118.         return "HeroNode [no=" + no + ", name=" + name + "]";
  119.     }
  121.     //前序遍历
  122.     public void preOrder() {
  123.         System.out.println(this);//先输出父节点
  124.         //递归向左子树前序遍历
  125.         if(this.left != null) {
  126.             this.left.preOrder();
  127.         }
  128.         //递归向右子树前序遍历
  129.         if(this.right != null) {
  130.             this.right.preOrder();
  131.         }
  132.     }
  134.     //中序遍历
  135.     public void midOrder() {
  136.         //递归向左子树中序遍历
  137.         if(this.left != null) {
  138.             this.left.midOrder();
  139.         }
  140.         System.out.println(this);//输出父节点
  141.         //递归向右子树前序遍历
  142.         if(this.right != null) {
  143.             this.right.midOrder();
  144.         }
  145.     }
  147.     //后序遍历
  148.     public void postOrder() {
  149.         //递归向左子树后序遍历
  150.         if(this.left != null) {
  151.             this.left.postOrder();
  152.         }
  153.         //递归向右子树前序遍历
  154.         if(this.right != null) {
  155.             this.right.postOrder();
  156.         }
  157.         System.out.println(this);//输出父节点
  158.     }
  160.     //递归删除结点
  161.     //1.如果删除的节点是叶子节点，则删除该节点
  162.     //2.如果删除的节点是非叶子节点，则删除该子树
  163.     public void delNode(int no) {
  164.         //思路
  165.         /*
  166.          *     1. 因为我们的二叉树是单向的，所以我们是判断当前结点的子结点是否需要删除结点，而不能去判断当前这个结点是不是需要删除结点.
  167.             2. 如果当前结点的左子结点不为空，并且左子结点 就是要删除结点，就将this.left = null; 并且就返回(结束递归删除)
  168.             3. 如果当前结点的右子结点不为空，并且右子结点 就是要删除结点，就将this.right= null ;并且就返回(结束递归删除)
  169.             4. 如果第2和第3步没有删除结点，那么我们就需要向左子树进行递归删除
  170.             5.  如果第4步也没有删除结点，则应当向右子树进行递归删除.
  171.          */
  172.         //2. 如果当前结点的左子结点不为空，并且左子结点 就是要删除结点，就将this.left = null; 并且就返回(结束递归删除)
  173.         if(this.left != null && this.left.no == no) {
  174.             this.left = null;
  175.             return;
  176.         }
  178.         //3.如果当前结点的右子结点不为空，并且右子结点 就是要删除结点，就将this.right= null ;并且就返回(结束递归删除)
  179.         if(this.right != null && this.right.no == no) {
  180.             this.right = null;
  181.             return;
  182.         }
  184.         //4.我们就需要向左子树进行递归删除
  185.         if(this.left != null) {
  186.             this.left.delNode(no);
  187.         }
  189.         //5.则应当向右子树进行递归删除
  190.         if(this.right != null) {
  191.             this.right.delNode(no);
  192.         }
  193.     }
  194. }

2.4 控制台输出

11.二叉树 - 图3