// 此章为数据结构学习笔记,对于算法的自然语言描述部分不会涉及
// 图片均来源于网络
// 动态 gif 图解各种排序算法
1. 排序的基本概念
1. 稳定性
稳定性是对于序列中有两个及以上相同关键字来说的,即若序列中有两个 50 ,记作 50(a) 和 50(b),两个 50 在序列中相邻,若排序后两个 50 依然相邻,我们说是稳定的,若任何一种情况使之顺序变化则不稳定。
对于关键字不重复,排序结果是唯一的,则无需考虑稳定的问题。
note
- 不稳定算法口诀:心情不稳定,快(**快速排序)些(希尔排序)选(直接选择排序)一堆(堆排序**)好友聊天吧
2. 排序算法的分类
| 分类 | 说明 | 具体算法 | 时间复杂度(平均情况) | 空间复杂度 |
|---|---|---|---|---|
| 插入类排序 | 在已经有序的序列中插入关键字,形成新的序列 | 直接插入排序 | n^2 | 1 |
| 折半插入排序 | 平均:n^2 最好:nlog2n 最坏:n^2 |
1 | ||
| 希尔排序 | 记:nlog2n | 1 | ||
| 交换类排序 | 每一轮排序经过一个交换动作,把一个关键字排到它最终的位置上 | 冒泡排序 | 最坏:n^2 最好:n |
1 |
| 快速排序 | 最好:nlog2n 最坏:n^2 |
log2n(递归,利用了系统栈) | ||
| 选择类排序 | 每一轮排序,选择出最小(最大)的关键字,把它和第一个(最后一个)关键字交换 | 简单选择排序 | n^2 | 1 |
| 堆排序 | nlog2n | 1 | ||
| 归并类排序 | 两个或两个以上有序序列合并成一个新的有序序列 | 二路归并排序 | nlog2n | n |
| 基数类排序 | 基于多关键字排序。比如对于一个班的学生,先按成绩排序,分为 A,B,C 三等,再分别在三组中按身高排序 | 多关键字排序 | d(n+r_d) | r_d |
记忆口诀:教官说:快(**快速排序)些(希尔排序**)以的速度归(**归并排序)队(堆排序**)。其余的都是 O(n^2)
3. 插入类排序
1. 直接插入排序
思想
直接插入排序就是将无序序列中的数和有序序列中的数进行比较,将无序序列的数插入到有序序列中去。
其中第一个位置默认为有序。 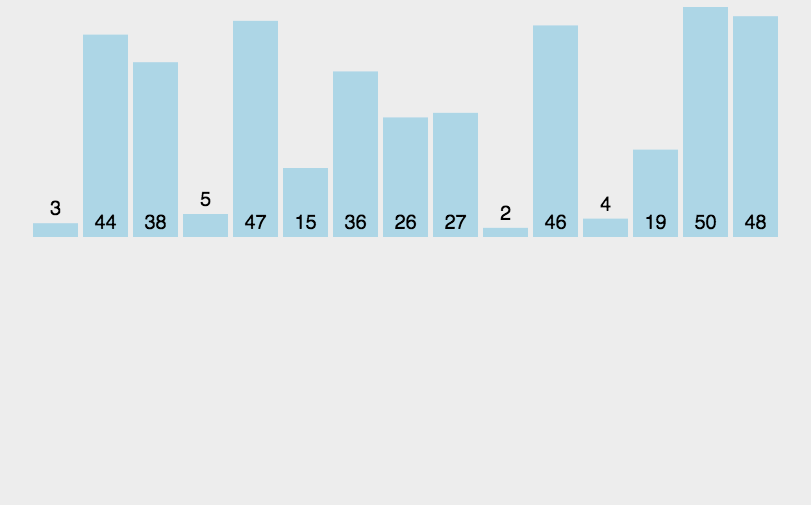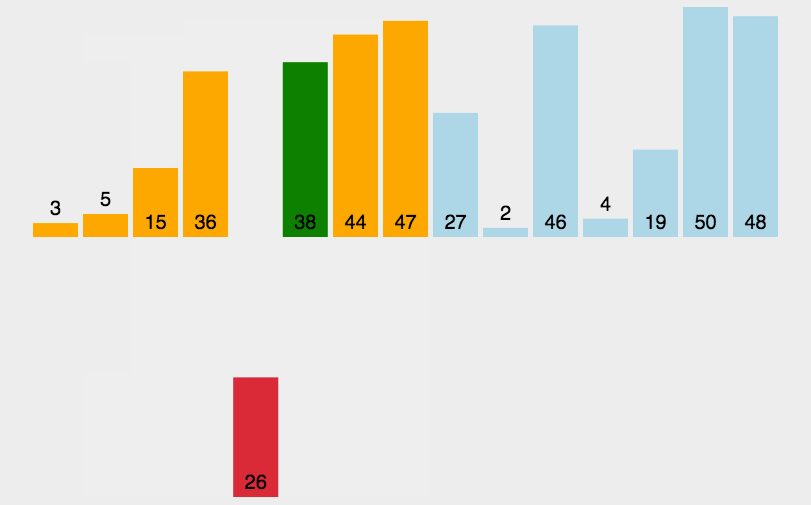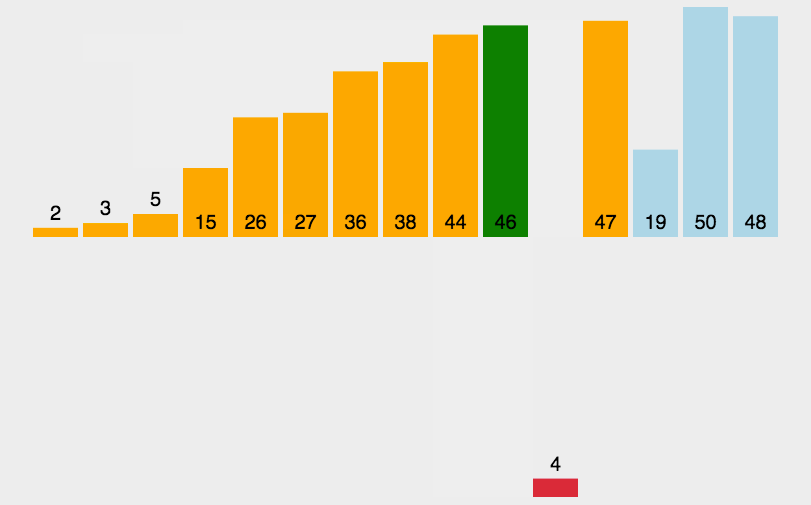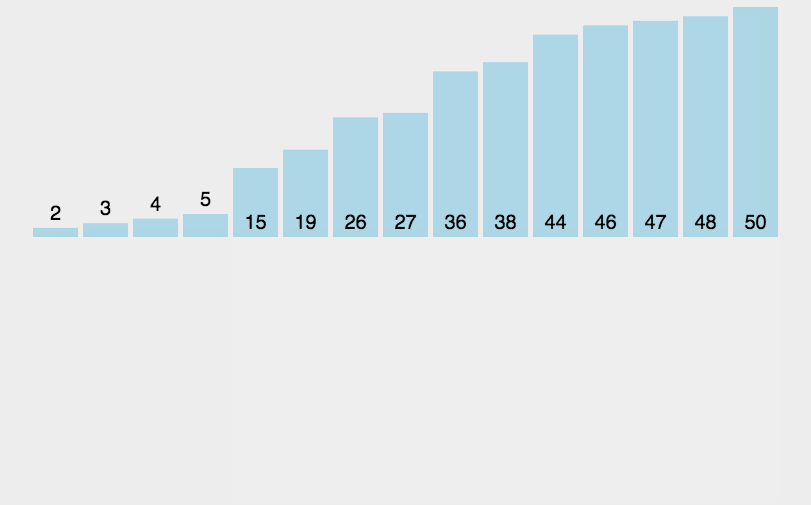
算法实现
#include <stdio.h>main(){int R[8] = {49,38,65,97,76,13,27,49};int temp;int i,j;// 排序代码// i = 1,因为让第一个数字处于了有序序列中(抽象的)for(i=1;i<10;i++){// temp 存放每轮比较的关键字temp=R[i];// j 用于定位与关键字比较的前一个元素// 设置 j 变量的原因是,因为在进行第 i 轮比较的时候// 不能去改变 i 的值,所以需要其他变量来改变j=i-1;// 当被比较的操作数位置未“向左”越界// 且关键临时值比已排好序的部分的每轮比较值小的时候// 进行移动while(j>=0&&temp<R[j]){R[j+1]=R[j];--j;}R[j+1]=temp;}// 打印输出for(i=0;i<8;i++){printf("%d ",R[i]);}}
时间和空间复杂度
时间复杂度:可以看到主要的耗时操作在于两个循环,且都是线性逼近而非非线性逼近,所以 O(n)。
空间复杂度:该算法没有引入新的存储空间,所以 O(1)。
2. 折半插入排序
考点手工排序
思想
- 基本条件:序列已经有序
- 判断标志:low > high
时间和空间复杂度
时间复杂度:在寻找插入位置上的时间大大减少,但是关键字移动上的时间不变。
最好情况:O(nlogn);最坏情况:O(n);平均情况:O(n)。
空间复杂度:同样没有引入新的存储空间,所以 O(1)。
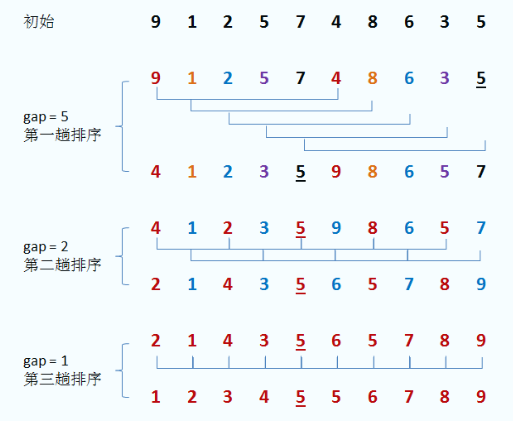
3. 希尔排序(增量)
思想
将待排序序列按照某种增量规则分为几个子序列,分别对子序列里的数值进行直接插入排序。
接着选取新的增量(比上一次的增量小),继续按直接插入排序,在新的子序列中排序。
最后选取增量为 1 的增量进行直接插入排序。
- 希尔排序的每次增量排序都使序列更有序
- 希尔排序是不稳定的
NOTE
- 希尔排序的增量每次都比上一次的小
- 增量选取的规则(规则很多,常见的两个)
- ⌊n/2⌋:即每次增量除以 2 并向下取整,此时时间复杂度 O(n)**【选这个】**
- 2+1:k 大于 1,2+1 小于排序长度,此时时间复杂度 O(n)
- PS:每次向后数 ⌊n/2⌋ 不包括第一个
- 增量序列的最后一个值一定是 1
- 增量的值尽量选取没有除 1 以外的公因子(素数)
- 空间复杂度:O(1)
4. 小结
- 插入类排序并不能完成每一轮排序后就使关键字达到最终位置
3. 交换类排序
1. 冒泡排序
时间与空间复杂度
时间复杂度
最好情况:即 if 条件语句不成立,O(n)
最坏情况(平均情况):O(n)
空间复杂度
O(1)
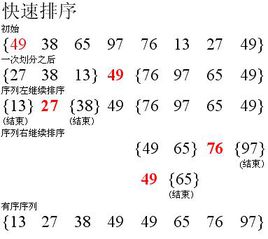
2. 快速排序(枢纽)
思想
- 性能高
- 分而治之
关键字选择序列中的第一个
首先选择第一个序列数值为枢轴
- 设置 i 和 j 的下标表示序列的第一个和最后一个数值
- 先从后往前,比较数值与枢轴的大小,若大于等于则不交换顺序,若小于则将该值取代枢轴
- 再从前往后,比较数值与枢轴的大小,若小于等于则不交换顺序,若大于则将该值取代枢轴
- 再递归执行上述步骤
- 直到序列有序
算法实现
#include <stdio.h>
void quick_sort(int s[], int l, int r);
main()
{
int R[8]={49,38,65,97,76,13,27,49};
quick_sort(R,0, 7);
for(int i=0;i<8;i++)
{
printf("%d ",R[i]);
}
}
//快速排序
void quick_sort(int s[], int l, int r)
{
// 这个 if 用于递归最后的结束条件
if (l < r)
{
// x 临时存储枢轴
// 这个地方对 l 和 r 都单独赋值
// 是因为最后递归调用的时候需要首项和末项
int i = l, j = r, x = s[0];
// 这个 whlie 用于一趟的循环
while (i < j)
{
while(i < j && s[j] >= x) // 从右向左找第一个小于x的数
j--;
// 并且执行完后 i 向左移 ,因为 i 不用比较这个刚拍好序的数
if(i < j)
s[i++] = s[j];
while(i < j && s[i] < x) // 从左向右找第一个大于等于x的数
i++;
// 并且执行完后 j 向左移
if(i < j)
s[j--] = s[i];
}
s[i] = x;
quick_sort(s, l, i - 1); // 递归调用
quick_sort(s, i + 1, r);
}
}
// 记忆技巧
// 外 if,内层一个 while 再嵌套两个 while
时间与空间复杂度
时间复杂度
最好情况(平均情况):O(nlonn)
最坏情况:O(n)
序列越无序效率越高,越有序效率越低
空间复杂度
O(logn),因为快排是递归进行,所以涉及到栈的辅助
4. 选择类排序
1. 简单选择排序(选无序之最小比有序之最后)
思想
从左至右扫描,选出最小的和有序序列的最后一个值进行交换
算法实现
#include <stdio.h>
main()
{
int R[8]={49,38,65,97,76,13,27,49};
int i,j,k,temp;
for(i=0;i<8;i++)
{
// 单独设置有序序列的下标
k=i;
for(j=i;j<8;j++)
{
// 如果该趟有序序列中最小值比
// 无序序列中还大
if(R[k]>R[j])
k=j;
}
// 交换值
temp=R[i];
R[i]=R[k];
R[k]=temp;
}
for(i=0;i<8;i++)
{
printf("%d ",R[i]);
}
}
时间和空间复杂度
时间复杂度:O(n)
空间复杂度:O(1)
2. 堆排序
二叉树部分性质回顾
因为堆排序需要用到二叉树的一些性质,在这里我们回顾以下需要用到的知识
- 双亲结点 = ⌊i/2⌋
- 如果 2i > n,那么结点无左孩子,否则 2i 就是左孩子
- 如果 2i+1 > n,那么 结点无右孩子,否则 2i+1 就是右孩子

思想
- 将堆看作是完全二叉树,满足任何一个非叶结点都大于(或者小于)左右孩子结点
- 如果最顶结点是最大值,则称为大顶堆;最小值,则称为小顶堆
堆排序最重要的操作是建堆(调堆)操作,以大顶堆为例
- 整体比较的顺序是按 i = len/2(此为第一个可能需要调整的结点) 后,从序列的第 i 项向前比较
- 叶子结点不考虑
- 从非叶子节点 i 开始( i = len/2 的这个结点开始),要求非叶子节点大于左右孩子结点,进行调整
- 找到这个 i 结点的左孩子(2i),先比较左右孩子,即 2i 和 2i+1,选取最大值和 i 进行比较
算法实现
// 总的调度程序
// 堆排序的第一个存储空间不用于排序存储
// 建堆是从下往上,而调堆是从上往下
void HeapSort(int A[],int len)
{
// 建大顶堆
BuildMaxHeap(A,len);
// n-1 趟交换和调堆
for(i=len;i>1;i--)
{
// 堆顶与堆底的交换
int temp = A[i];
A[i]=A[1];
A[1]=temp;
AdjustDown(A,1,i-1);
}
}
// 建堆
void BuildMaxHeap(int A[],int len)
{
// 从最大的非叶结点开始调整
// len/2 是最大的(下标)非叶结点(双亲结点)
// 以下操作的本质就是跳过叶子结点开始调堆
for(int i=len/2;i>0;i--)AdjustDown(A,i,len);
}
// 调堆
// k 是要检查的结点
// 就是某个下脚处的部分调整
void AdjustDown(int A[],int k,int len)
{
// A[0] 不初始值,所以可以用来存子树范围内要检查的子树根结点
A[0]=A[k];
// 从左孩子开始比较
for(i=2k;i<=len;i*=2)
{
// 左右孩子比较,若右孩子大,则比较右孩子与双亲
if(i<len&&A[i]<A[i+1])i++;
// 如果这个结点的值不小于它的孩子结点,则不交换
if(A[0]>=A[i])break;
else
{
A[k]=A[i];
// i 赋值给 k 继续往下调整
k=i;
}
}
// 和开头对称
A[k]=A[0];
}
时间和空间复杂度
时间复杂度:O(nlogn)
空间复杂度:O(1)
5. 二路归并排序
思路
分而治之
- 将原始序列看作是 n 各只含一个关键字的子序列,则每个序列有序
- 两两归并形成若干有序二元组
- 再将二元组看成是若干有序子序列
- 继续两两归并
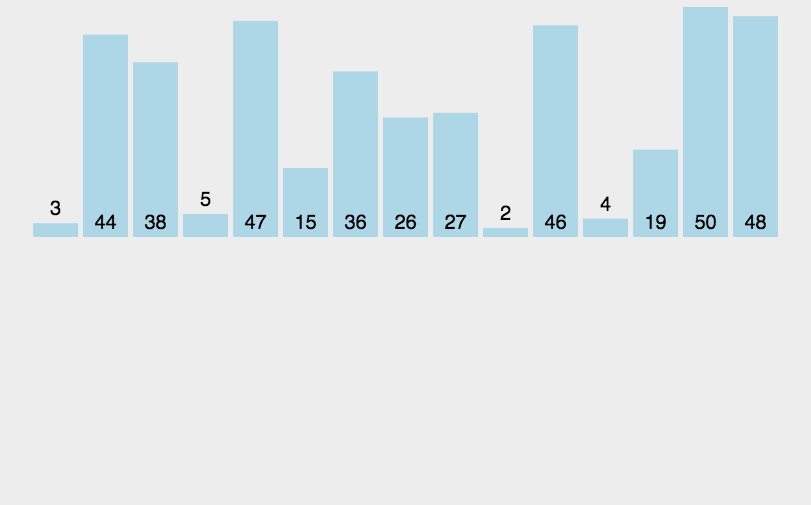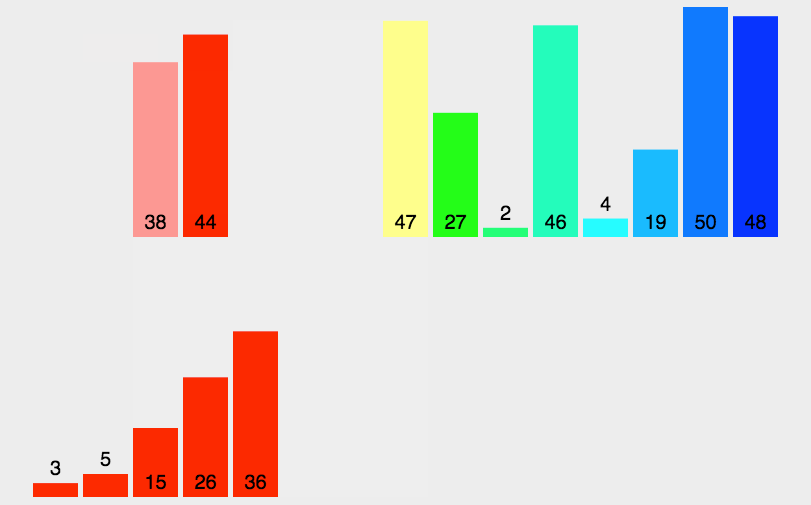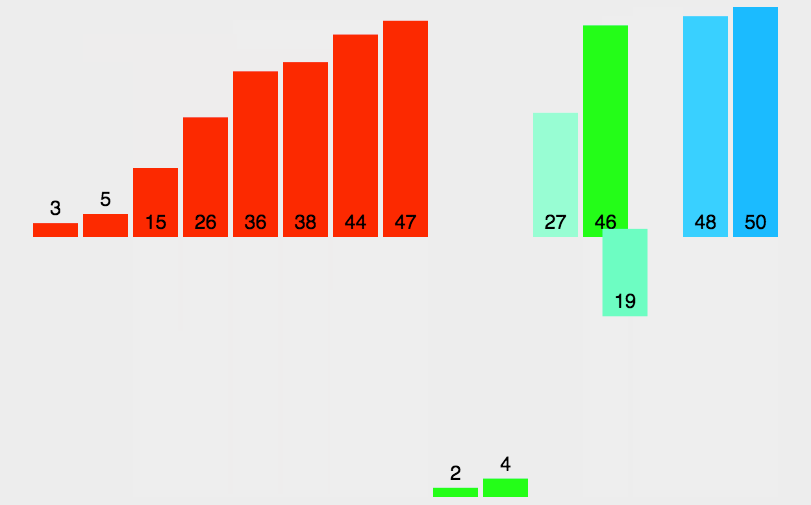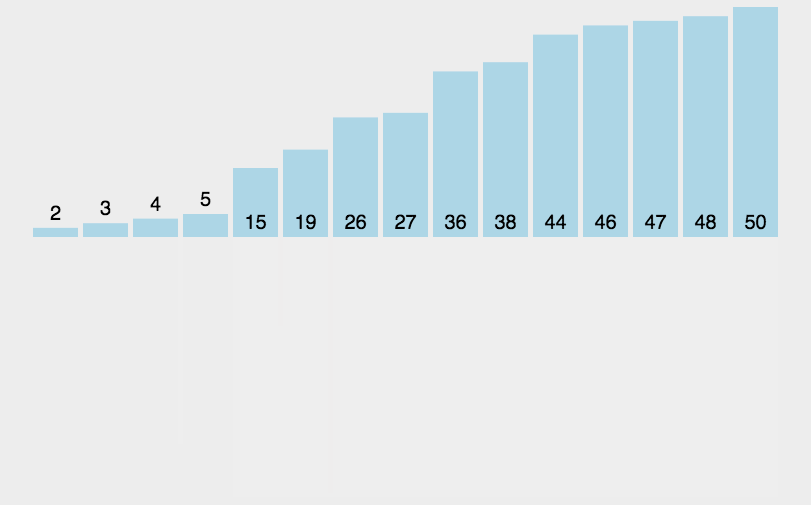
算法代码
#include <stdio.h>
void MergeSort(int R[],int low,int high);
void Merge(int R[],int low,int mid,int high);
main()
{
int R[8]={49,38,65,97,76,13,27,49};
MergeSort(R,0,7);
for(int i=0;i<8;i++)
{
printf("%d ",R[i]);
}
}
// 无限划分,即划分到子序列只有 1 个元素的情况时,
// 就可以开始归并了
void MergeSort(int R[],int low,int high)
{
if(low<high)
{
int mid = (low+high)/2;
MergeSort(R,low,mid);
MergeSort(R,mid+1,high);
// 每一次递归层级内执行归并
Merge(R,low,mid,high);
}
}
void Merge(int R[],int low,int mid,int high)
{
// 设置临时数组
int B[100];
int i,j,k;
// 先将 R 数组中的全部元素复制给 B 数组
// 但是实际上我们只会用到每次归并排序的部分
for(i=low;i<=high;i++)B[i]=R[i];
// k 变量用于指示 R 数组每次被从 B 数组中选出的值
// 应该填充的位置
// i<=mid&&j<=high 只要满足任意合并的数组被比较完
// 也就说明其他部分顺序已经是确定的了
for(i=low,j=mid+1,k=i;i<=mid&&j<=high;k++)
{
if(B[i]<=B[j])R[k]=B[i++];
else R[k]=B[j++];
}
// 将剩余的数值复制过来
while(i<=mid)R[k++]=B[i++];
while(j<=high)R[k++]=B[j++];
}
时间与空间复杂度
最好,最坏,平均:O(nlog2n)
空间复杂度
因为借用了额外数组,所以是 O(n)
6. 基数排序
思想
见算法书 籍
时间与空间复杂度
时间复杂度
最坏,平均:O(d(n+r))
空间复杂度
O(r)
特点
- 基数排序不需要进行关键字比较

7. 外部排序
基本概念
外部排序是对外存中的记录(记录,页)进行排序。因为外存中数据规模非常大,此时不能简单利用前面讲解的内部排序(前面所有的排序算法都是内部排序)的方式完成任务。 **
思想
- 假设有 n 个记录,我们把 n 个记录分为 m 个较小的记录段,并对这些记录段先各自排序,因为此时记录段较小,可以直接读入内存排序
- 将这 m 个记录段又每 k 段分为一组,每次取一组进行外部排序

(如改图所示,共有 75 个记录,每 10 个记录左右(即不一定完全是 10 个)分为一段,每 3 段分为一组,所以 k = 3;比如,此时有 75 个学生,每 10 个学生分成一个小组,每 3 个小组分成一个大组)
- 每次我们从红色矩形框中,把该列的数据导入内存进行比较,将最小的数值输出,被输出的空缺位由同行下一个元素填补
- 重复 3 步骤,直到排序完
- 整个这样的流程我们叫 k 路归并,如下图为 3 路归并,之前还讲过 2 路归并。

(效果 gif 所示)
子算法
整个外部排序是一种思想,而外部排序中还包含了其他的子算法
置换选择排序
观察上面的分段图,你会发现,每一个子段已经被排好序了,那么这些子段是如何排好序的呢,这就是采用了置换选择排序。

最佳归并树
我们在每次归并操作的时候,每个记录都会进行 2 次 IO 操作,而 IO 操作是非常耗时的,利用最佳归并树提升效率
最佳归并树也叫多路哈夫曼树,即构造带权路径最小的哈夫曼树,使得其 IO 操作执行的次数最小
思想
如有以下长度的归并段:9,30,12,18,3,17,2,6,24
和构造哈夫曼树一样,最终的最佳归并树
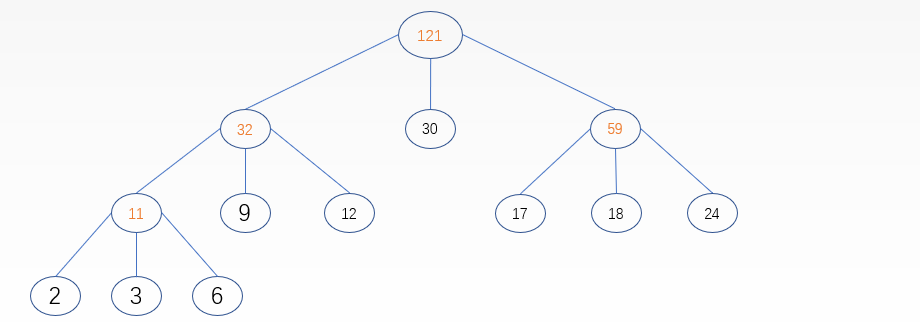
其 IO 操作的次数:I/O次数=2(23+33+63+92+122+301+172+182+242)=446
其中 2()表示每个记录每趟归并都要进行 2 次 IO 操作
其中 n3,表示,我们可以看到一共进行了 3 趟归并操作
败者树
当每趟各个段的首记录被送入内存进行排序的时候,我们觉得这样还是很浪费时间,尤其是当一组的归并段划分很多,那么每次比较的记录也会很多,这时就可以用败者树来优化时间复杂度

(整颗败者树的构造如图)
败者树排序过程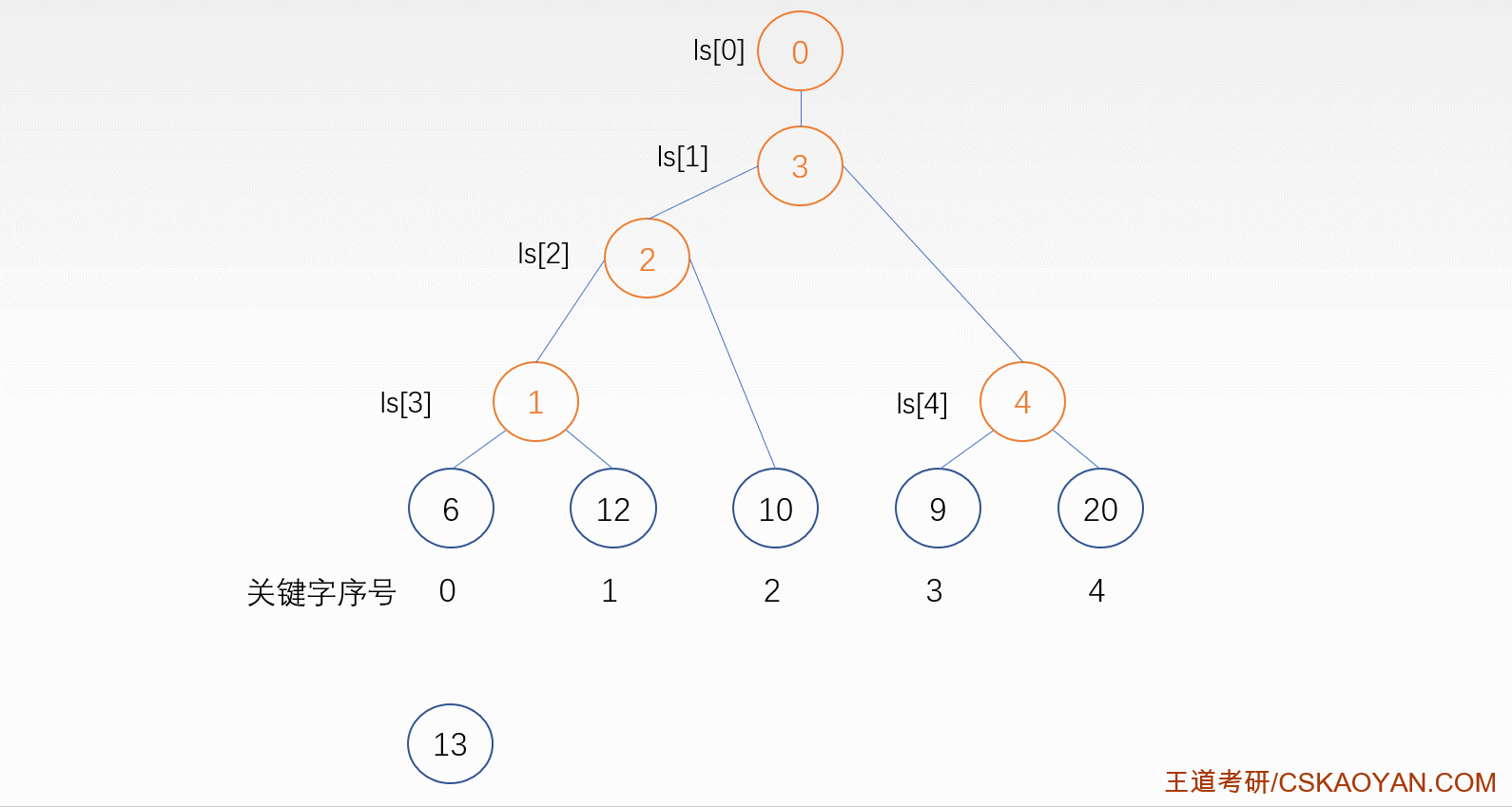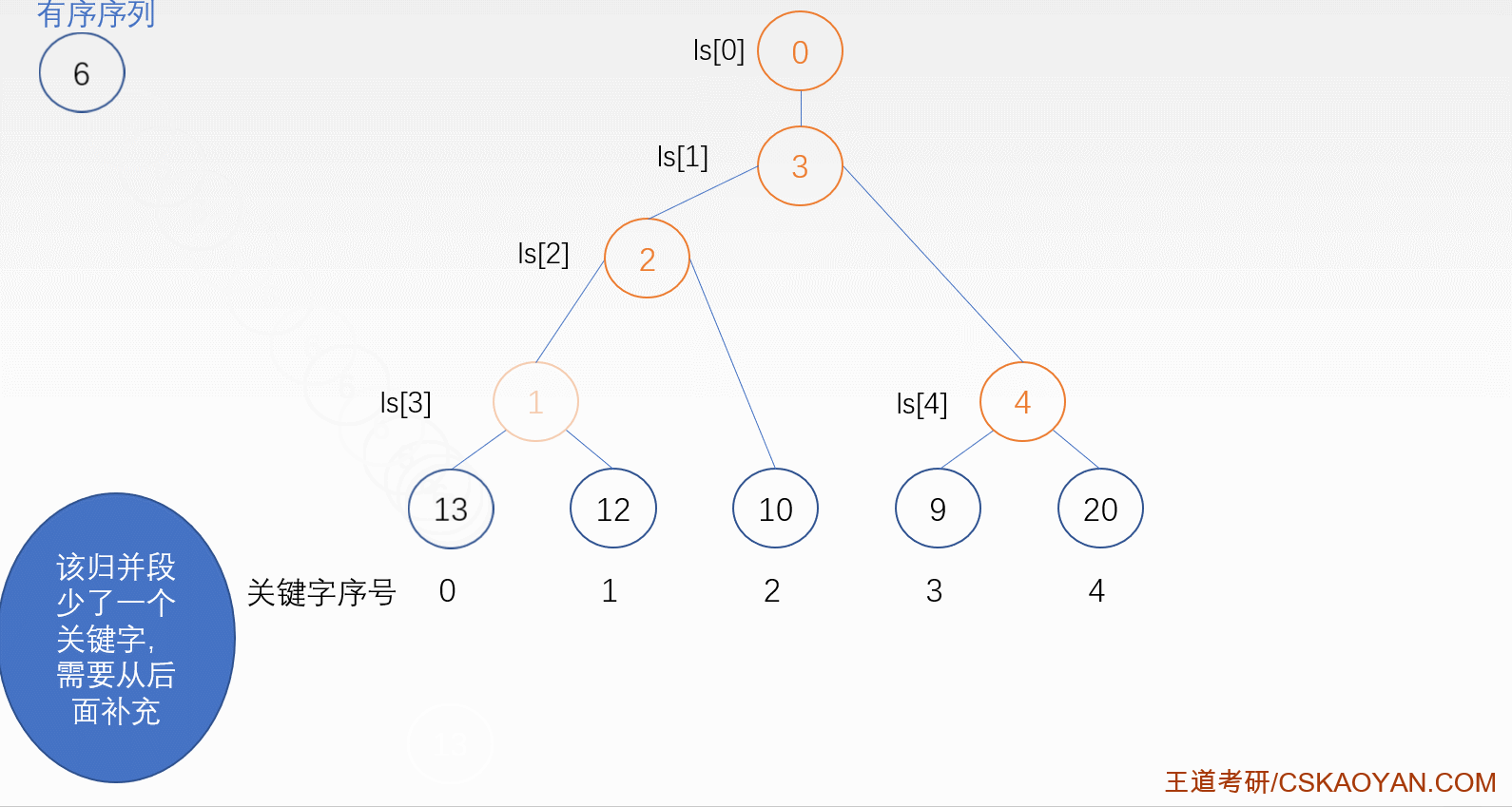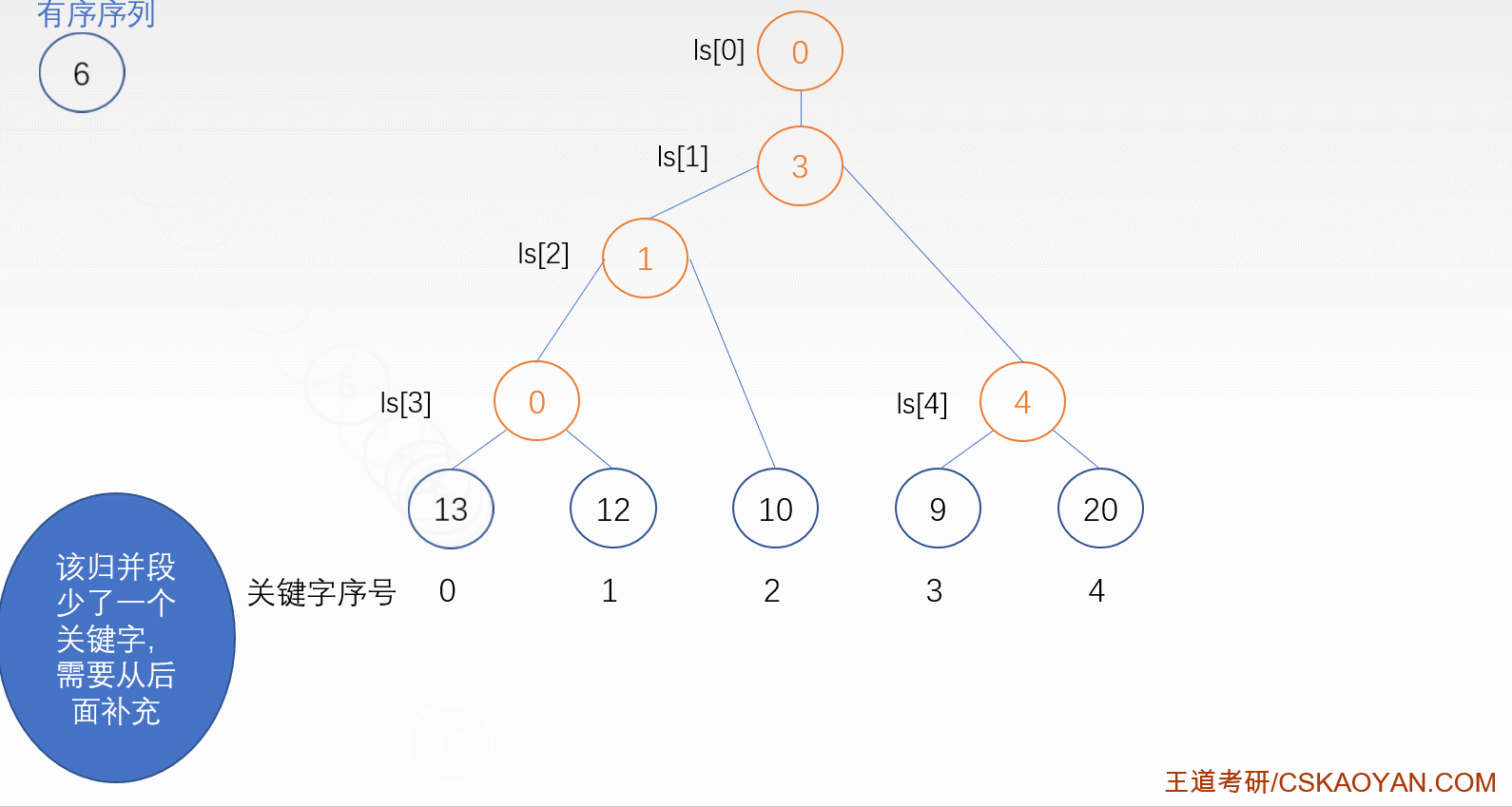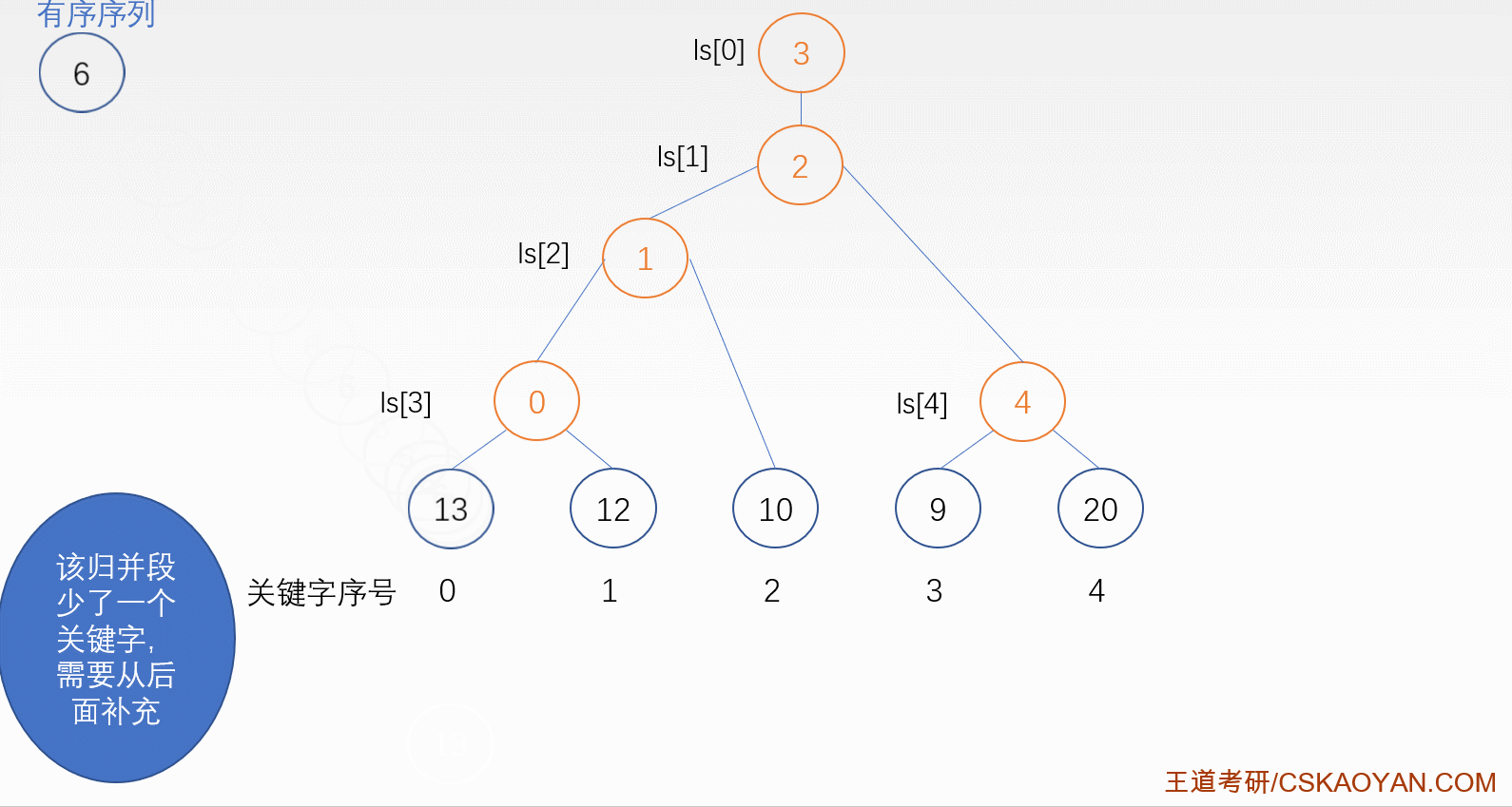
8. 补充
1.题型
- 已知 n 轮排序结果求排序算法,且题目未告知初始序列,只高速了结果
- 简单选择排序(无序之最小比有序之最大):n 轮之后应该前 n 项从小到大有序或后 n 项从大到小有序
- 冒泡排序:n 轮后,最小沉底或者最大冒出
- 直接插入排序(无序插入有序序列):n 轮后前 n 项有序
- 堆排序:n 轮后,筛选出 n 个从大到小或者从小到大的顺序
- 关键字比较次数与初始排列次序无关的是:简单选择排序。因为简单选择排序每一次都要一个一个挑选无序中的最小值。
- 排序效率的比较
- 快速排序在序列有序下退化成冒泡排序
- 堆排序和简单选择排序的时间复杂度与初始序列无关
- 每趟排序能够保证一个关键字到达最终位置:冒泡,快速,简单选择,堆
- 关键字比较次数与原始序列无关的:简单选择,折半插入
- 排序趟数,原始状态类型题目(图片来源)
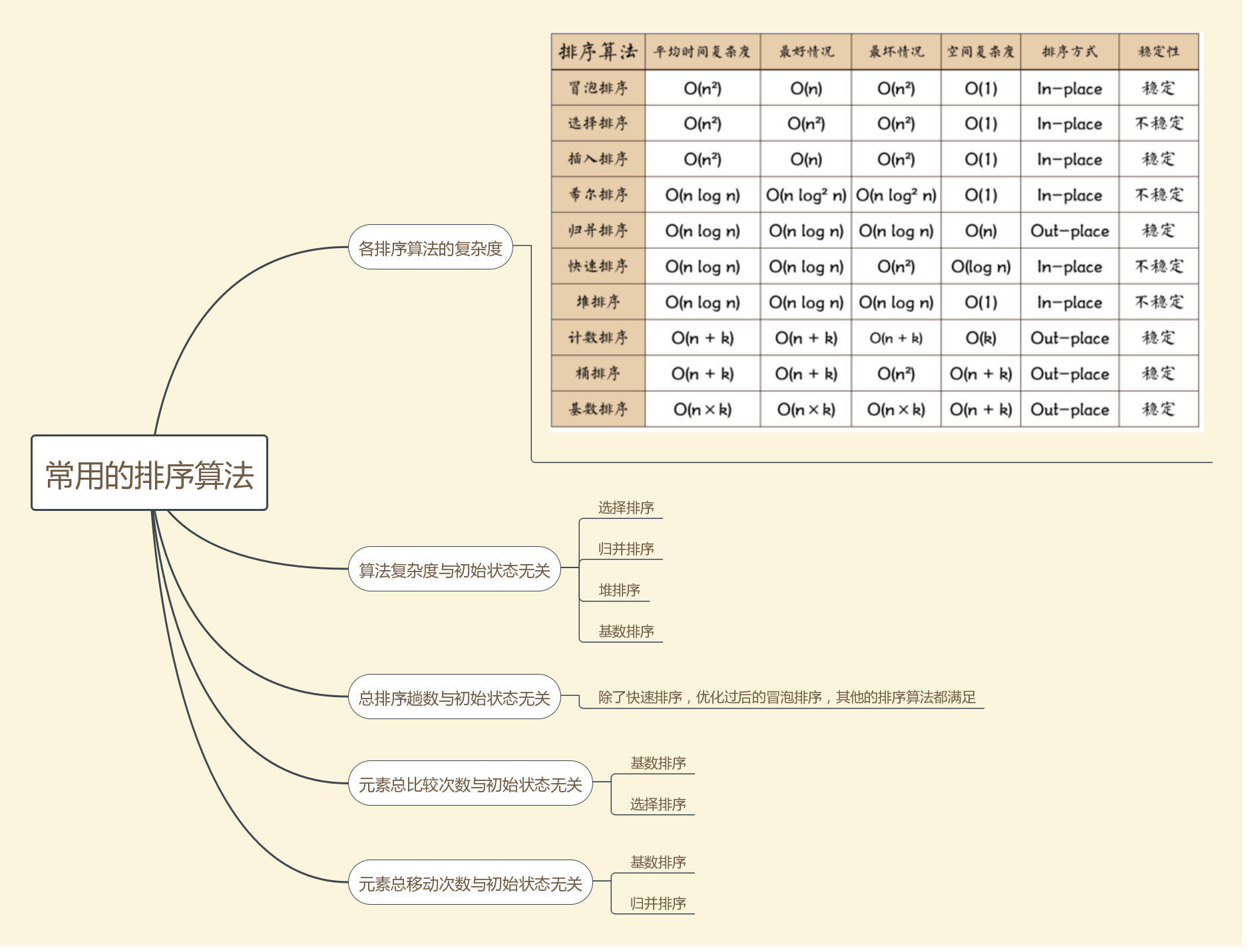
口诀:
- 复选归基堆(复选飞机堆)
- 趟快冒冒(有关)
- 比选基
- 移基归