1. 串的定义

1. 串的核心是字符
2. 空格串，是只包含空格的串，它和空串是有区别的，空格串有长度，且可以不止一个空格。

1. 顺序存储结构

note：

1. ch 是指针形式，因为我们要对其进行动态分配，但并不是链的形式
2. S.ch 是因为 S 本身不是指针，只有 S 本身是指针的时候才用 -> 访问其元素

2. 链式存储结构

2. 串的操作

串的比较通过字符的编码实现的，字符的编码是指字符在对应字符集中的序号。

2.1 如何比较两个串

比较原则

1. 如果是单个字符，按 ASCLL 比较
2. 如果是多个字符，长度相等，同样按 ASCLL 比较
3. 如果是多个字符，长度不等，短的更小

举例

1. “hap” < “happy”
2. “happen”<”happy”，因为 “y” > “e”，所以 happy 是大于 happen 的

int strcompare(Str s1,Str s2)
{
    for(int i=0;i<s1.length && i<s2.length;i++)
        if(s1.ch[i]!=s2.ch[i];
           return s1.ch[i]-s2.ch[i];
     return s1.length - s2.length;
}

2.2 赋值操作

串不能直接用 “=” 赋值，因为是数组

// 串的数据结构见 6.1 
int assignment(String *str,char *Character)
{
    // 先把要赋值到的内存空间清空
    if(str.ch)
        free(str.ch);
    char *c = Character;
    int len=0;
    // 统计 Character 即赋值源的字符信息
    while(c)
    {
        ++len;
        ++c; // 地址的增加
    }
    if(len==0)
    {
        str.ch=NULL;
        length=0;
        return 1;
    }
    else
    {
        // 开始分配操作
        str.ch = (char *)malloc(sizeof(char)*(len+1));
        // 如果分配空间失败
        if(str.ch==NULL)
            return 0;
        else
        {
            c=ch;
            for(int i=0;i<=len;i++)
                str.ch[i]=*c;
            str.length=len;
            return 1;
        }
    }
}

2.3 串连接操作

把两个串连接在一起的操作

int concat(Str *str,Str str1,Str str2)
{
    // 为防止意外，先清空此处的内存
    if(str.ch)
    {
        free(str.ch);
        str.ch=NULL;
    }

    str.ch=(char*)malloc(sizeof(char)*(str1.length+str2.length));
    if(str.ch==NULL)
        return 0;

    int i=0,j=0;
    if(i<str1.length)
    {
        str.ch[i]=str1.ch[i];
        ++i;
    }

    if(j<str2.length)
    {
        str.ch[i+j]=str2.ch[j];
        ++j;
    }

    str.length=str1.length+str2.length;
    return 1;
}

2.4 求子串的数目

2.5 判断子串是否出现在了主串中

3. 串的抽象数据类型

串关注的操作是查找字串的位置，得到指定位置的字串，替换字串。

StrAssign(T,*chars); // 生成一个其值等于字符串常量 chars 的串 T
StrCopy(T,S); // 串 S 存在，就复制串 S 到串 T
ClearString(S); // 串 S 存在，将串清空
StringEmpty(S); // 若串 S 为空，则返回 true
StrLength(S); // 返回串的元素个数，即串的长度
StrCompare(S,T); // 若 S>T，返回值大于 0；若等于，返回值等于 0；若小于，返回值小于 0
Concat(T,S1,S2); // 用 T 返回有 S1 和 S2 连接而成的新串
SubString(Sub,S,pos,len); // 串 S 存在，
                          // 1<=pos<=StrLength(S)
                          // 0<=len<=StrLength(S)-pos+1，这个地方 +1 是因为字符串是从 1 开始的

Index(S,T,pos); // 串 S 和串 T存在，T 为非空串，若主串 S 中存在和串 T 值相同的子串，则返回它在主串
                // S 中第 pos 个字符之后出现的位置，否则返回 0
                  // 也就是说这里 T 是子串
Replace(S,T,V); // 用 V 替换 S 中出现的所有与 T 相等且不重叠的子串
StrInsert(S,pos,T); // 在 S 的 pos 之前插入串 T
StrDelete(S,pos,len); // 从 S 中删除从第 pos 位置长度为 len 的子串

关于 Index 的实现

// 若主串 S 中第 pos 个字符之后存在与
// T 相等的子串，则返回第一个这样的子串在 S 
// 中的位置，否则返回 0
int Index(String S,String T,int pos)
{
    int n,m,i;
    String sub;
    if(pos>0)
    {
        n = StringLength(S);
        m = StringLength(T);
        i = pos;
        // n-m+1 表示必须要大于这个值，才能匹配 T
        // 的长度 
        while(i<=n-m+1)
        {
            SubString(sub,S,i,m);
            if(StrCompare(Sub,T)!=0)
                ++i;
            else 
                return i;
        }
    }
    return 0;
}

4. 朴素的模式匹配算法

子串的定位操作通常称作串的模式匹配。

具体的匹配过程参见《大话数据结构》

简单来说就是对主串的每一个字符做子串开头，与要匹配的字符串进行匹配，对主串做大循环，对每个字符开头做 T 的长度的小循环。

利用朴素模式匹配算法实现查找子串

// 若主串 S 中第 pos 个字符之后存在与
// T 相等的子串，则返回第一个这样的子串在 S 
// 中的位置，否则返回 0
int Index(String S,String T,int pos)
{
    // i 用于标识主串 S 当前位置的下标，若
    // pos 不为 1，则从 pos 位置开始匹配 
    int i=pos;

    // 用于标识 T 的位置的下标 
    int j=1;
    int pos=i;

    // S[0] 和 T[0] 中标识 S 和 T 的长度，串的实际数值从位置 1 开始
    while(i<=S[0]&&j<=T[0]) 
    {
        if(S[i]==T[i])
        {
            ++i;
            ++j;
        } 
        else
        {
            // 如果不匹配，则返回 S 之前开始
            // 的下标的下一个位置，期待下一次匹配 
            i=pos++;
            // j 返回 T 的首位 
            j=1;
        }
    } 
    if(j>T[0])
        return i-T[0];
    else    
        return 0; 
}

该算法的问题是效率太低了。

5. KMP 算法

具体内容参见《大话数据结构》
阮一峰讲 KMP
两种类型的 KMP 计算题：《王道》《408 15 8）

5.1 next 数组和 nextval 数组的推导

见《大话数据结构》P139（PDF P164）

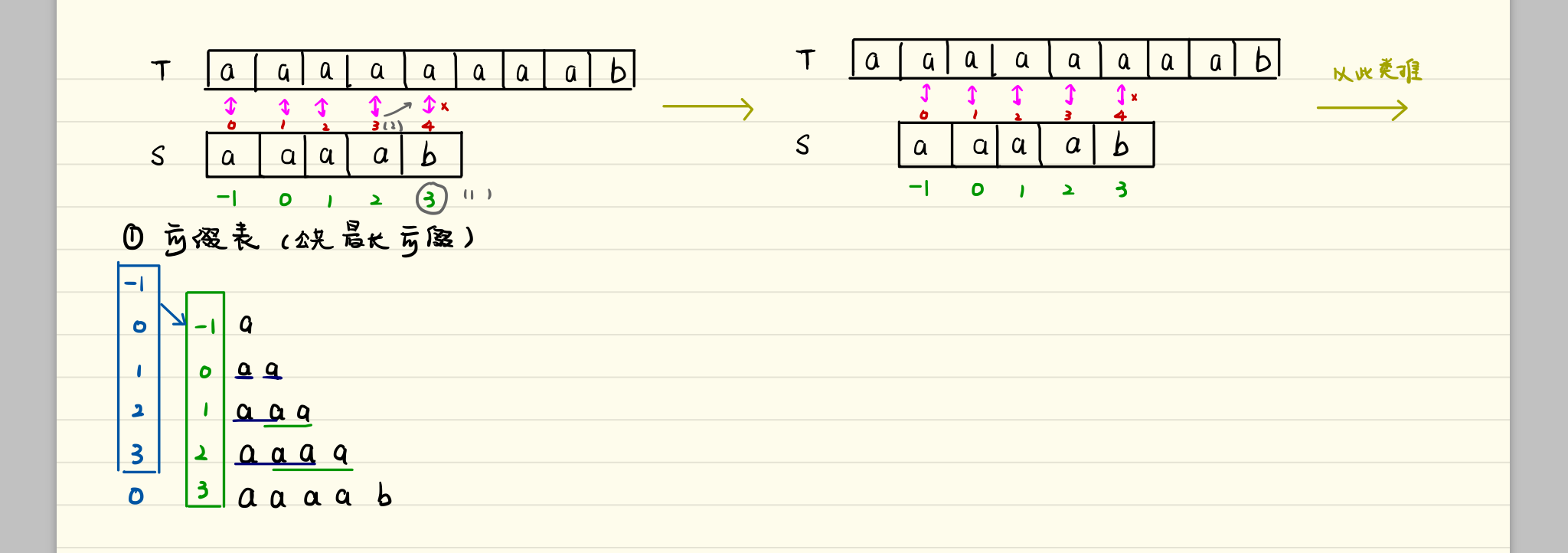
KMP 步骤

1. 建立部分匹配表（前后缀匹配表）
2. 当遇见不匹配的字符时，开始计算向后移动位数
3. 移动位数 =已匹配的字符数 - 最后一位匹配到的字符对应的部分匹配表的数字

void get_next(String T,int *next)
{
    int i,j;
    i=1;
    j=0;
    next[1]=0;
    // 此处 T[0] 表示 T 的长度
    while(i<T[0])
    {
        // T[i]表示后缀的单个字符
        // T[j]表示前缀的单个字符 
        if(j==0 || T[i]==T[j])
        {
            ++i;
            ++j;
            next[i]=j;
        }
        else
            j=next[j]; // 字符不相同对 j 进行回溯 
    }
}

int Index_KMP(String S,String T,int pos)
    {
        // i 是 S 当前位置的下标 
        int i=pos;
        // j 是 T 当前位置的下标 
        int j=1;
        int next[255];
        get_next(T,next);
        while(i<=S[0]&&j<=T[0])
        {

            if(j==0||S[i]==T[j])
            {
                ++i;
                ++j;    
            }
            else
            {
                // 返回 j 的回溯位置 
                j=next[j];
            }
        } 
        if(j>T[0])
            return i-T[0];
        else 
            return 0;
    }

6. 补充

6.1 串的数据结构

// 定长
typedef struct 
{ 
    // 多加的 1 是 '\0' 的结束位置 
    char string[maxSize+1];
    int length;
}String;

// 变长
typedef struct
{
    char *string;
    int length;
}String;

// 变长的方式需要使用 malloc 分配空间