1. 数组

1. 基本介绍

  1. 存储方式：顺序存储
  2. 常考题目计算题：数组元素的下标计算（偏移量）
    1. 行优先
    2. 列优先

2. 行优先和列优先

  1. 行优先：即行按从左至右的顺序被填满
  2. 列优先：即列按从上至下的顺序被填满

2. 矩阵的压缩存储

1. 矩阵

矩阵的表示

int A[m][n];
PS：

  1. m，n 的取值
    1. 常量
    2. 宏定义的量

矩阵的转置

思路：设置一个新的矩阵，把转置后的矩阵放进去

  1. #include <stdio.h>
  2. void transposition(int A[][3],int B[][2],int a,int b);
  4. main()
  5. {
  6.     int a=2;
  7.     int b=3;
  8.     // 二维数组可以不指定第一维，但必须指定第二维
  9.     // 如 A[][3]，是正确的
  11.     // 初始化二维数组时，后面的值也可以写的更完整，如{{1,2,3},{4,5,6}} 这样的形式，便于
  12.     // 阅读 
  13.     int A[2][3] = {1,2,3,4,5,6};
  14.     int B[3][2] = {0};
  16.     // 二维数组作为参数传递，直接给变量名即可，这是在传递
  17.     // 二维数组的首地址 
  18.     transposition(A,B,a,b);     
  19. }
  21. void transposition(int A[][3],int B[][2],int a,int b)
  22. {
  23.     printf("转置前：\n");
  24.     for(int i=0;i<a;i++)
  25.     {
  26.         for(int j=0;j<b;j++)
  27.         {
  28.             printf("%d ",A[i][j]);
  29.         }
  30.         printf("\n");        
  31.     }
  33.     for(int i=0;i<a;i++)
  34.     {
  35.         for(int j=0;j<b;j++)
  36.             B[j][i] = A[i][j];
  37.     }
  39.     printf("转置后：\n");
  40.     for(int i=0;i<b;i++)
  41.     {
  42.         for(int j=0;j<a;j++)
  43.         {
  44.             printf("%d ",B[j][i]);
  45.         }
  46.         printf("\n");        
  47.     }
  50. }

控制台运行
转置前：
1 2 3
4 5 6
转置后：
1 2
4 5
2 3

矩阵的加法

思路：按数学中矩阵的加法运算即可

#include <stdio.h>
#define maxSize 3

void add(int A[][maxSize],int B[][maxSize],int c[][maxSize],int a,int b);
main()
{
//    3 行 3 列的数组
    int a=3;

    int A[3][3] = {1,2,3,4,5,6,7,8,9};
    int B[3][3] = {1,2,3,4,5,6,7,8,9};
    int C[3][3] = {0};     

    add(A,B,C,a,a);
}

void add(int A[][maxSize],int B[][maxSize],int c[][maxSize],int a,int b)
{
    int i,j;
    // 显示数组 A 
    printf("数组 A：\n");
    for(i=0;i<a;i++)
    {
        for(j=0;j<b;j++)
        {
            printf("%d ",A[i][j]);
        }
        printf("\n");
    }
    printf("\n-----------------");

    // 显示数组 B 
    printf("数组B：\n");
    for(i=0;i<a;i++)
    {
        for(j=0;j<b;j++)
        {
            printf("%d ",B[i][j]);
        }
        printf("\n");
    }
    printf("\n-----------------");

    // 显示数组 C
    printf("数组C：\n");
    for(i=0;i<a;i++)
    {
        for(j=0;j<b;j++)
        {
            printf("%d ",B[i][j]+A[i][j]);
        }
        printf("\n");
    }     
}

控制台运行
数组 A：
1 2 3
4 5 6
7 8 9
————————-数组B：
1 2 3
4 5 6
7 8 9
————————-数组C：
2 4 6
8 10 12
14 16 18

特殊矩阵与稀疏矩阵

对称矩阵

满足条件 a = a 的矩阵称为对称矩阵

存储
对称矩阵因为其特性，所以只用存储下三角型的数据，这样存储空间就减半了，存储的数据个数为， 第六章 数组，矩阵与广义表 - 图1

对称矩阵在一维数据中的存储
image.png
几个特殊的下标

  1. a，元素在数组中下标为 0，是第 1 个元素
  2. 左下角元素 a，下标为 n(n-1)/2 ，是第 {n(n-1)/2}+1 个元素
  3. 右下角元素 a 下标是 {(1+n)n/2}-1

三角矩阵

三角矩阵根据数学定义，其存储方式只需在对称矩阵的一维存储数组中，增加一个存储空间，用于存放重复三角部分的元素 C （C 常常为 0），这个 C 就是上三角矩阵的 0
image.png
image.png

稀疏矩阵

稀疏矩阵是指元素中 0 元素特别多，且分布不均匀的矩阵（这是一个抽象的数学概念，具体稀疏还是稠密是相对的）

1. 顺序表示法
  1. 三元组（NOTE：三元组的存储元素的行列均从 0 开始）
  2. 伪地址表示法

1.1 利用三元组记录和创建矩阵

三元组包含的分量（非零元素个数，稀疏矩阵的行数，稀疏矩阵的列数）

#include <stdio.h>

void createThree(int A[][4],int B[][3],int row,int col);
void printB(int B[][3]);

main()
{
    int A[][4]={0,0,0,1,
                  0,0,3,2,
                  1,0,0,0,
                  0,2,0,0};
//    这里 B 的列数是 3 ，因为是三元组，只有
//    三个相关列 
    int B[][3]={};
    createThree(A,B,4,4);
    printB(B);
}

// 将矩阵 A 存储成 三元组 B 
void createThree(int A[][4],int B[][3],int row,int col)
{
    int k=1;
    int i,j;
    for(i=0;i<row;i++)
    {
        for(j=0;j<col;j++)
        {
            if(A[i][j]!=0)
            {
                // 核心代码，当该元素不为零时
                // 在三元组中记录其值，行号，列号（行列号都是从 0 开始）
                B[k][0]=A[i][j];
                B[k][1]=i;
                B[k][2]=j;
                ++k;
            }
        }
    }

    // 这里需要减一，因为一开始 k 是设置的 1 
    // 第 0 行记录三元组的相关信息（有效数据个数，有效数据行数和列数）
    B[0][0]=k-1; // 存储的有效数据的个数
    B[0][1]=row;
    B[0][2]=col; 

    for(i=0;i<k;i++)
    {
        for(j=0;j<3;j++)
        {
            printf("%d  ",B[i][j]);
        }
        printf("\n");
    }
    printf("\n");
}

// 将三元组 B 打印成矩阵
void printB(int B[][3])
{
    int k=1;
    int i,j;
    for(i=0;i<B[0][1];i++)
    {
        for(j=0;j<B[0][2];j++)
        {
            if(i==B[k][1] && j==B[k][2])
            {
                printf("%d ",B[k][0]);
                k++; 
            }
            else
            {
                printf("0 ");
            }
        }
        printf("\n");
    }
}

1.2 伪地址表示法

思想
利用相对位置来表示

存储
一行只有两个存储单元，分别存放数值和地址

计算方法
第六章 数组，矩阵与广义表 - 图5 用于计算相对位置

2. 链式表示法
  1. 邻接表表示法
  2. 十字链表表示法

2.1 邻接表表示法

规则
每一行非零元素串成一个链表，链表结点由两个分量（数值，列数）

（图片来源）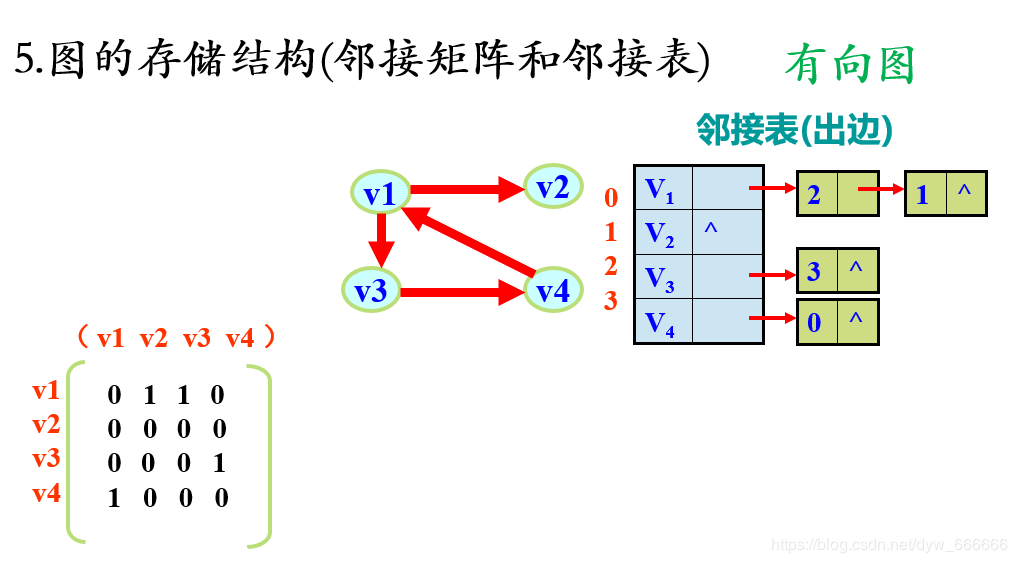
第六章 数组，矩阵与广义表 - 图6

note：这里的邻接表和图中的邻接矩阵用法类似

2.2 十字链表表示法

结点结构
行分量，列分量，值，指向下方指针（矩阵中以行为准的下一个元素），指向右方指针（同一行的后面的元素）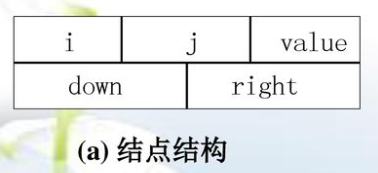
image.png

实例
这里行列数都是从 1 开始的。

（图片源于网络，侵删）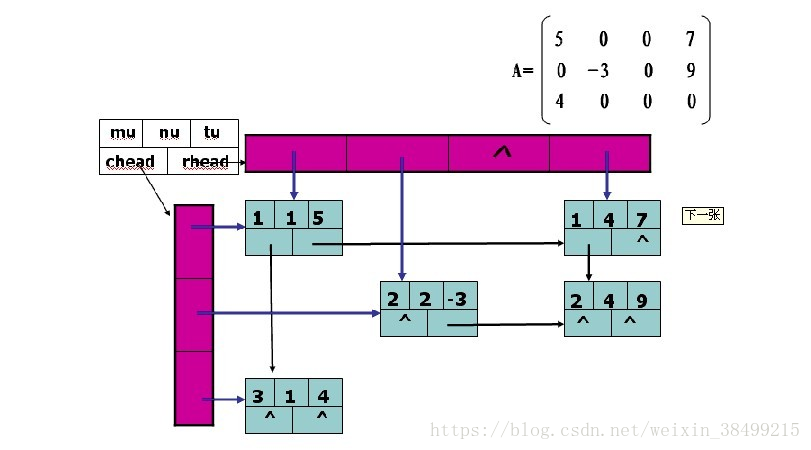
第六章 数组，矩阵与广义表 - 图8

3. 广义表

1. 定义

  1. 表元素是原子或者广义表的一种线性表的扩展结构。用于存储像 {1,{1,2,3}} 这样不合适用数组存储的形式
  2. 广义表又叫做列表，是一种线性存储结构，里面既可以存储不在分割的元素，也可以存储（可分割）广义表
  3. 单个元素称为原子，内部的广义表成为子表

2. 性质

  1. 长度：表中最上层元素的个数
  2. 深度：表中括号的最大层数，需要将子表展开
  3. 表头：第一个元素为广义表的表头
  4. 表尾：其余元素为表尾，如 {1，{1，2，3}，4} 中，1 是表头，{1，2，3}，4 又组成一个子表为表尾

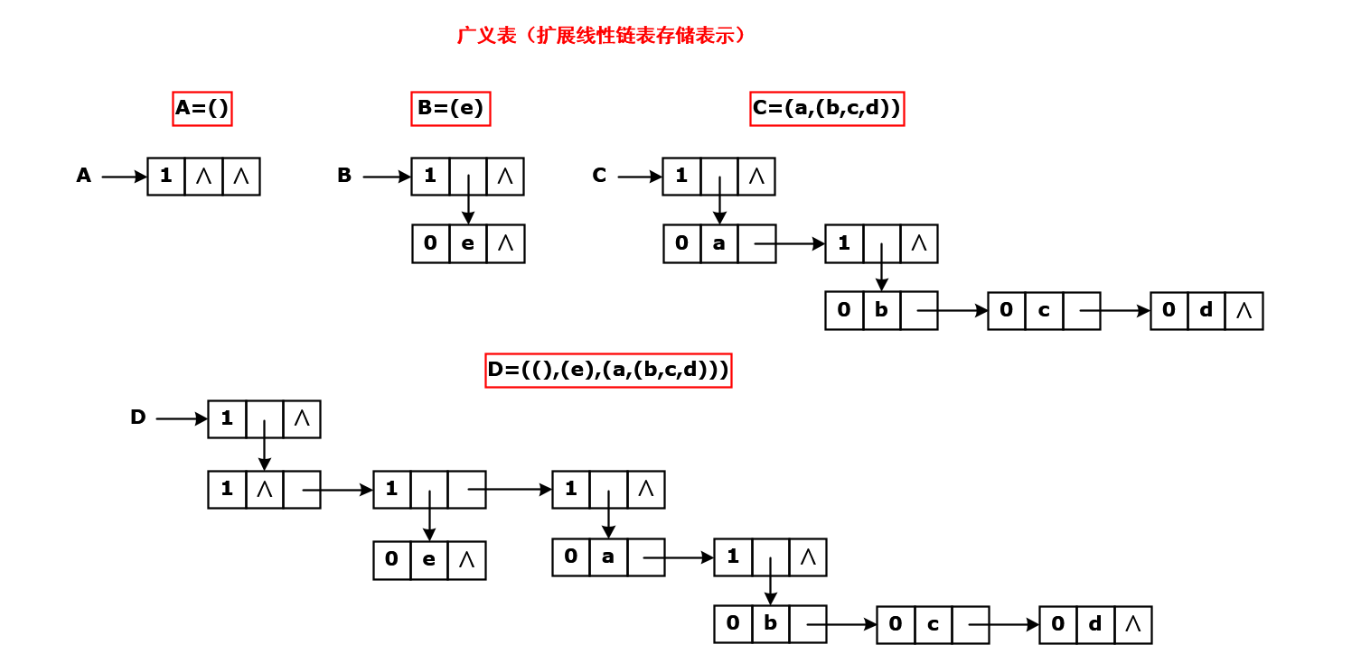
以下是广义表存储数据的一些常用形式：

  • A = ()：A 表示一个广义表，只不过表是空的。
  • B = (e)：广义表 B 中只有一个原子 e。
  • C = (a,(b,c,d)) ：广义表 C 中有两个元素，原子 a 和子表 (b,c,d)。
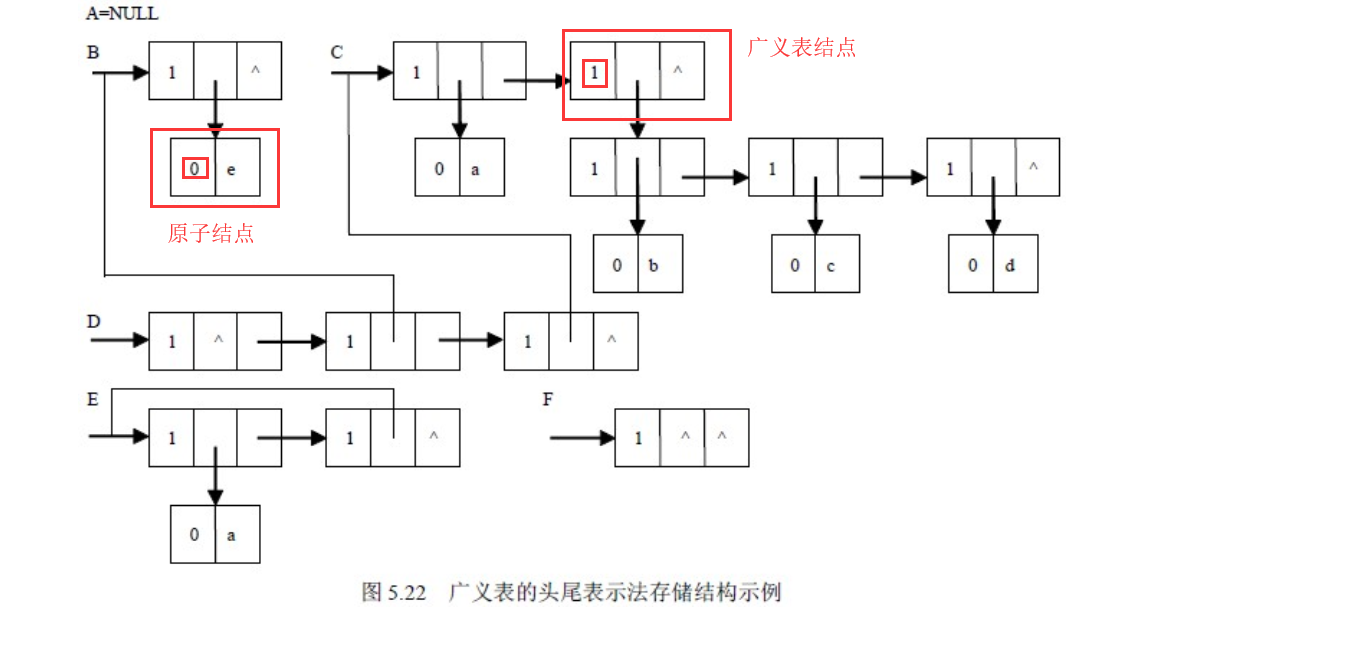
  • D = (A,B,C)：广义表 D 中存有 3 个子表，分别是A、B和C。这种表示方式等同于 D = ((),(e),(b,c,d)) 。
  • E = (a,E)：广义表 E 中有两个元素，原子 a 和它本身。这是一个递归广义表，等同于：E = (a,(a,(a,…)))。

3. 头尾链表存储结构

  1. 结点
    1. 原子结构
      1. 标记域：0 时为原子，1 时为广义表
      2. 数据域
    2. 广义表结构
      1. 标记域
      2. 头指针域：指向原子或者广义表
      3. 尾指针域：指向本层下一个广义表

image.png

4. 扩展线性表存储结构

  1. 原子结点
    1. 标记域
    2. 数据域
    3. 尾指针域
  2. 广义表结点
    1. 标记域
    2. 头指针域
    3. 尾指针域

image.png