前言 绪论

note：

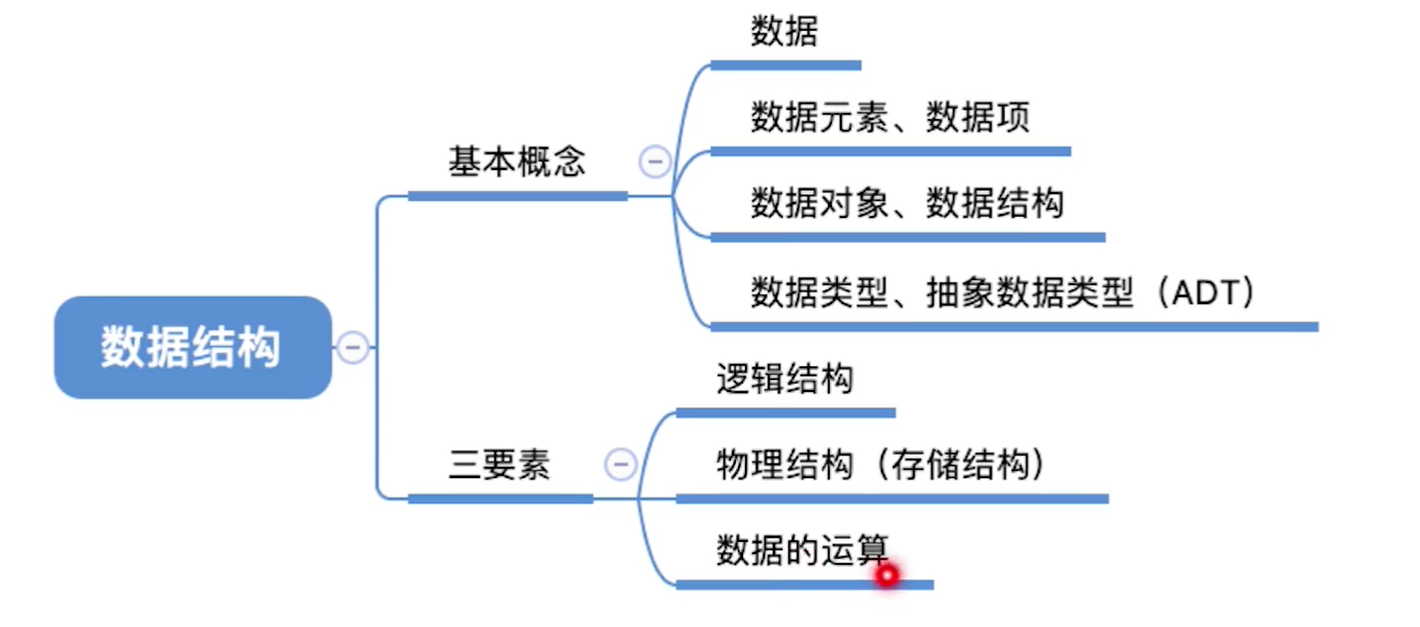
1. 顺序存储物理上是连续的，非顺序存储，物理上可以是非连续的
2. 存储结构对数据运算（操作）产生影响
3. 之所以讨论存储结构是为了在物理世界（计算机）中实际运行我们的数据
4. 讨论数据结构的顺序：逻辑结构->对数据的操作->存储结构（物理结构）
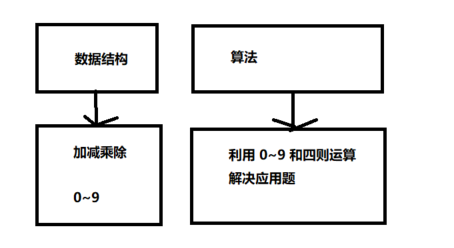
5. 算法与数据结构之间的关系：

第一节 算法复杂度

1.定义与术语

1. T(n)：语句总的执行次数 T 与问题规模 n 之间的函数关系。T(n) 随 n 的变化从而确定 n 的数量级
2. O(n)：时间复杂度，记作 T(n) = O(f(n))，算法执行时间的增长率和 f(n) 的增长率相同，称作渐进时间复杂度，简称时间复杂度。其中 f(n) 是问题规模 n 的某个函数
3. 用 O() 来体现时间复杂度，我们称之为大 O 记法
4. 算法是一个问题求解步骤的描述
5. 原地工作，还需要额外空间

2.推导大 O 阶与时间复杂度

2.1步骤

1. 去掉常数项
2. 去掉低阶项，只保留最高项
3. 置最高项系数为 1

2.2 常数阶

常数阶常常是顺序结构

int sum = 0,n = 100; // 只执行了一次
sum = (1+n)*n/2;     // 只执行了一次
printf("%d",sum);    // 只执行了一次

所以 f(n) = 3，根据推导过程，结果是 O(1)

2.3 线性阶

int i;
for(i-0;i<n;i++)
{//执行的步骤}

结果是 O(n)，通常一个的循环为线性阶

2.4 对数阶

int count = 1;
while (count<n)
{
    count = count*2;
}
// O(nlog2n)
for(k=1;k<n;k*=2)
{
    f(j=0;j<n;j++);
}

由于每次 count 乘以 2 之后，就距离 n 更近了一点，也就是说多少次 2 相乘后会大于 n 呢，由 2 = n 推出 x = logn，所以结果是 O(logn)。
通常，一个循环结构和一个前后 n 倍关系的顺序结构结果得到对数阶。

2.5 平方阶

int i,j;
for(i=0;i<n;i++)
{
    for(j=0;j<n;j++)
    {
        // 执行步骤
    }
}
for(i=0;i<n;i++)
{
    for(j=0;j<m;j++)
    {
        // 执行步骤
    }
}

第一个大循环块的结果是 O(n)，第二个大循环块的结果是O(m*n)

int i,j;
for(i=0;i<n;i++)
{
    for(j=i;j<n;j++)
    {
        // 执行步骤
    }
}

分析：当 i=0 时，内循环了 n 次，当 i = n-1 时，内循环了 n-1 次，以此类推，我们得到
根据大 O 推导方法，最终结果是 O(n)

2.8 算法执行时间与输入数据有关

2.7 常见的时间复杂度

1. 常见的时间复杂度

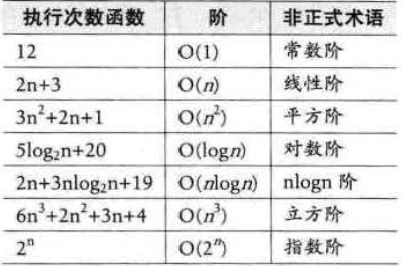
1. 时间复杂度耗时排行榜

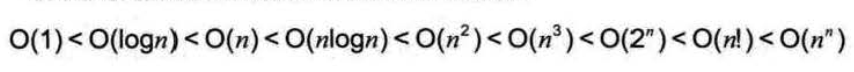
常对幂指阶，时间越来越多咧

3.最坏情况与平均情况

最坏情况：通常指的运行时间
平均情况：期望的运行时间

4. 如何分析时间复杂度的补充

1. 忽略顺序执行的代码，因为这些是常数项，只分析循环部分
2. 嵌套结构，只看最里面，且最里面为外层的乘积结果

第二节 空间复杂度

一般我们不讨论空间复杂度

第三节 基本概念

1. 算法的基本概念

1. 算法的特性
   1. 有穷性
   2. 确定性：相同的输入，必须得到相同的输出
   3. 输入
   4. 输出
   5. 可行性

2.数据结构的基本概念

1. 物理结构（存储结构）
   1. 顺序结构
      1. 顺序存储
      2. 链式存储
   2. 非顺序结构
      1. 索引存储
      2. 散列存储

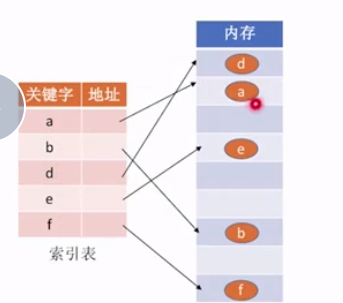(索引存储)