1 定义
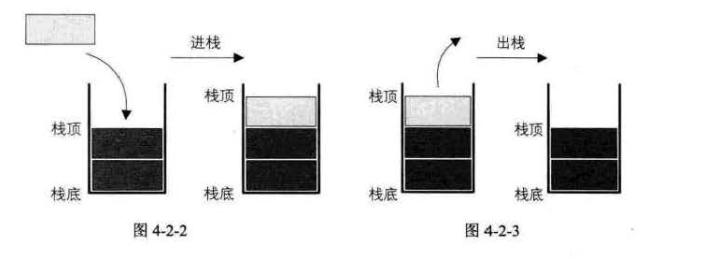
- 栈是只能在表尾(栈顶)进行插入和删除的线性表
- 队列是只能在一端插入,而在另一端删除的线性表
2 栈
1. 基本概念
- 栈的插入:进栈,压栈或者入栈
- 栈的删除:出栈,弹栈
- 栈的数学性质,n 个元素以某种顺序进栈,则其出栈的可能排列:
2. 进栈出栈的变化
PS:并不是最先进栈的元素就是最后出栈的
3. 抽象数据类型
InitStack(*S); // 初始化一个空栈DestroyStack(*S); // 销毁一个存在栈ClearStack(*S); // 清空一个栈StackEmpty(S); // 判断栈空GetTop(S,*e); // 若栈非空,返回栈顶值Push(*S,e); // 将新元素 e 插入到 S 中,并成为栈顶元素Pop(*S,*e); // 删除栈顶元素,并返回其值StackLength(S); // 返回 S 的元素个数
4. 栈的顺序结构及其实现 顺序栈相比于链栈是重点
- 栈的顺序结构称为顺序栈,其中下标为 0 的一端为栈底。top 指示栈顶元素的位置。
- 若存储栈的长度为 StackSize ,则 top 必须小于 StackSize。
- 只有一个元素存在 top = 0;没有元素存在(空栈),top = -1。
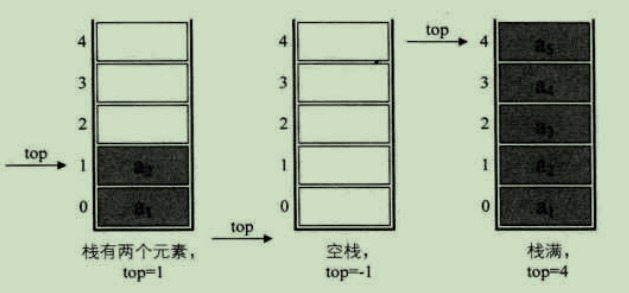
顺序栈的数据结构
typedef struct{// 存放栈的元素int data[maxSize];// 栈顶指针int top;} SqStack;
4.1 两个状态
// 栈空st.top = -1;// 栈满st.top = maxSize-1;
4.2 顺序栈的初始化
void init(Sqstack *st){st->top = -1;}
4.3 进栈操作
// 核心就两句代码st.top++;st.data[st.top]=x;Status Push(SqStack *S,SElemType e){// 判断栈满if(S->top == MAXSIZE -1)return 0;S->top++;S->data[S->top]=e;return 1;}
4.4 出栈操作
// 核心代码就两句x = st.data[st.top];st.top--;// 出栈操作Status Pop(SqStack *S,SElemType *e){if(S->top == -1) // 空栈return 0;// 把要出栈的元素先拷贝出来*e=S->data[S->top];S->top--;return 1;}
4.5 两栈共享
让一个栈的栈底为数组的始端(即下标为 0),另一个栈为栈的末端(下标为数组长度 n-
)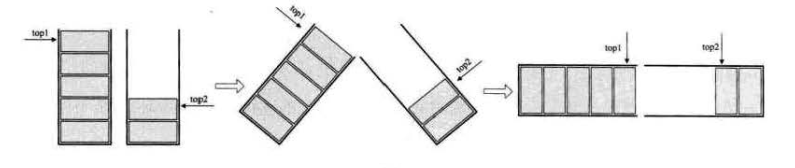
PS:top 1 和 top 2 是栈顶指针,只要两者不相等,那么栈就可以继续使用。
空栈
当 top1=-1 时,左栈为空;当 top2 = n 时,右栈为空。
满栈
若右栈为空,当左栈 = n-1 时,左栈全满。
若左栈为空,当右栈 = 0 时,右栈全满。
top1 + 1 == top2 是否相等,若相等则满
部分代码实现
// 共享栈数据结构
typedef struct
{
int elem[maxSize];
// top[0] 表示第一个栈,top[1] 表示第二个栈
int top[2];
}SqStack;
// 进栈操作
// stackNumber 是进栈号,即进入哪一个栈
int push(SqStack *st,int stackNumber,int x)
{
// 首先判断栈满
if(st.top[0]+1==st.top[1])
return 0;
// 若栈不满则进栈
if(stackNumber==1)
{
++(st.top[0]);
st.elem[st.top[0]] = x;
return 1;
}
else if(stackNumber==2)
{
--(st.top[1]);
st.elem[st.top[1]] = x;
return 1;
}
}
// 出栈操作
int pop(SqStack *st,int stackNumber,int x)
{
if(stackNumber==1)
{
// 判断栈空
if(st.top[0]==-1)
return 0;
x = st.elem[st.top[0]];
--(st.top[0]);
return 1;
}
else if(stackNumber==2)
{
// 判断栈空
if(st.top[1]==maxSize)
return 0;
x = st.elem[st.top[1]];
--(st.top[1]);
return 1;
}
// 若栈号都不是则退出
return 0;
}
5. 栈的链式存储结构及实现
- 链栈中栈顶放在单链表的头部,并且不需要头结点。
- 链栈不存在栈满的情况。
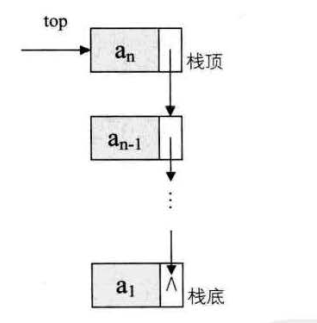
5.1 几个状态
// 栈空
lst->next=NULL;
// 栈满
链栈不存在栈满的情况(假设内存无限)
5.2 链栈的结构与链栈初始化
typedef struct LNode
{
int data;
struct LNode *next;
}LNode;
// 初始化
void init(LNode *lst)
{
lst = (LNode*)malloc(sizeof(LNode));
lst->next = null;
}
另一种链栈的初始化
![[1RZ}]]I%U%%$5]H4UX5(6.png
5.3 进栈操作(等于单链表的头插法)
思想
top 指向元素值为 e 的新结点,s 的直接后继为原 top 指向的结点。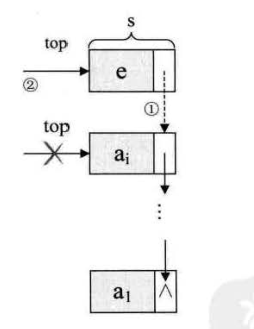
// 核心代码
p->next=lst->next;
lst->next=p;
void push(LNode *lst,int x)
{
// 创建要插入的新结点 p
LNode *p;
p = (LNode *)malloc(sizeof(LNode));
p->next=null;
// 将 p 插入到 lst 头结点的后面,并赋值
p->data = x;
p->next = lst->next;
lst->next = p;
}
5.4 出栈操作
思想
将栈顶指针下一一位:S->top = S->top->next;
释放 p(要被删除的结点):free(p);
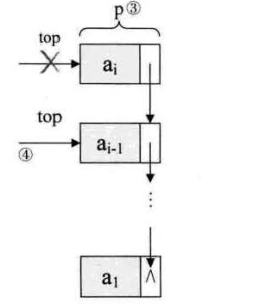
// 核心代码
p->next=lst->next;
lst->next=p->next;
free(p);
// 出栈操作
Status Pop(LNode *lst,int x)
{
LNode *p;
// 检查是否栈空
if(lst->next==NULL)
{
return 0;
}
p = lst->next;
lst->next = p->next;
free(p);
return 1;
}
6. 递归
- 递归就是自己调用自己
- 你可以这样简单的理解递归,那就是被调用的函数不是自己,而是另一个函数,不过和自己长得一模一样
- 正式因为栈的特殊结构,使得利用栈来实现递归会非常的合适
函数调用的背后
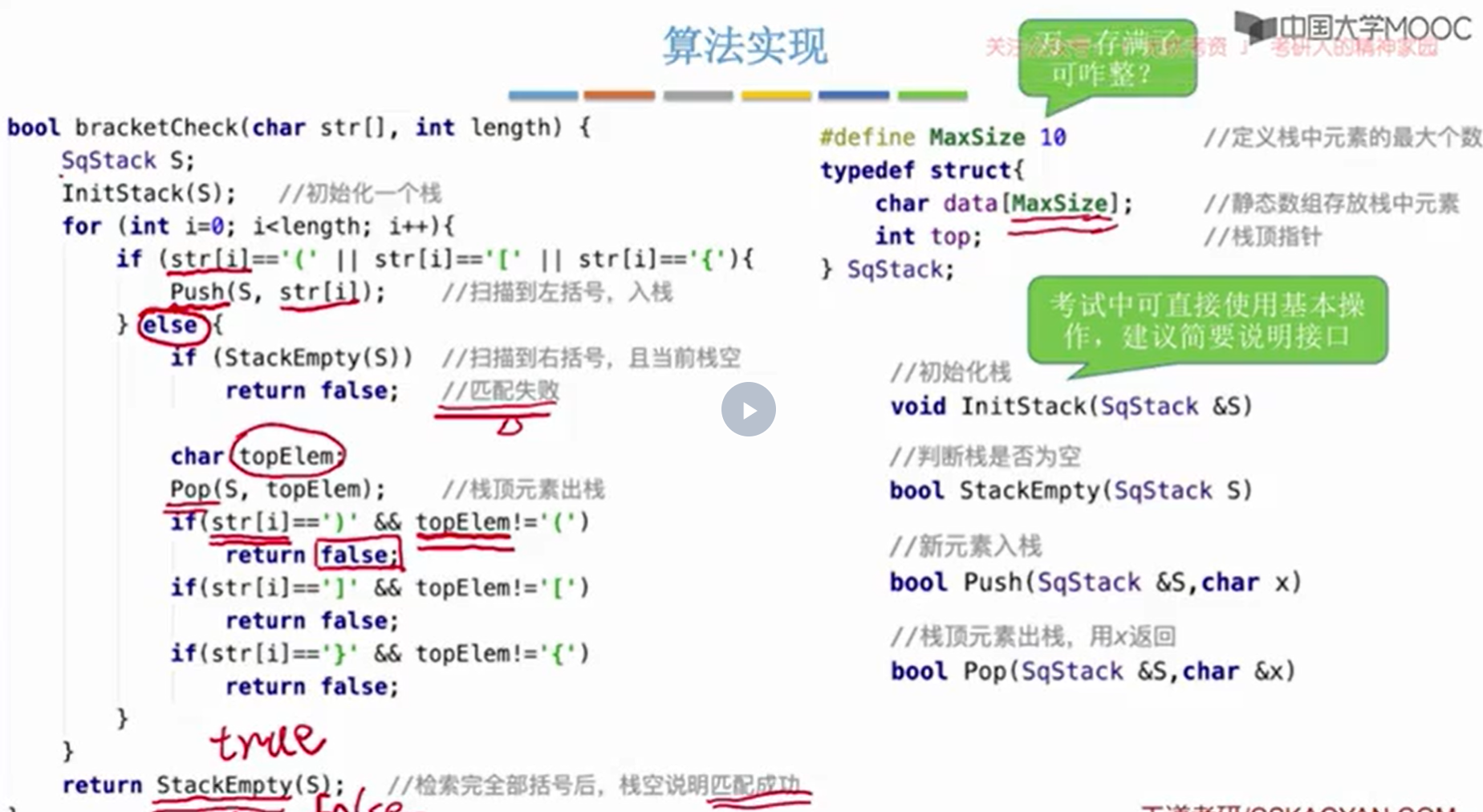
核心思想:每一个左标号压入栈中,每遇上一个右标号就检查匹配,匹配则出栈,否则失败。
括号匹配失败:
- 栈空,但还有下一个右标号
- 栈不空,但左右标号不匹配
- 栈残留,匹配完了,还剩一个左标号
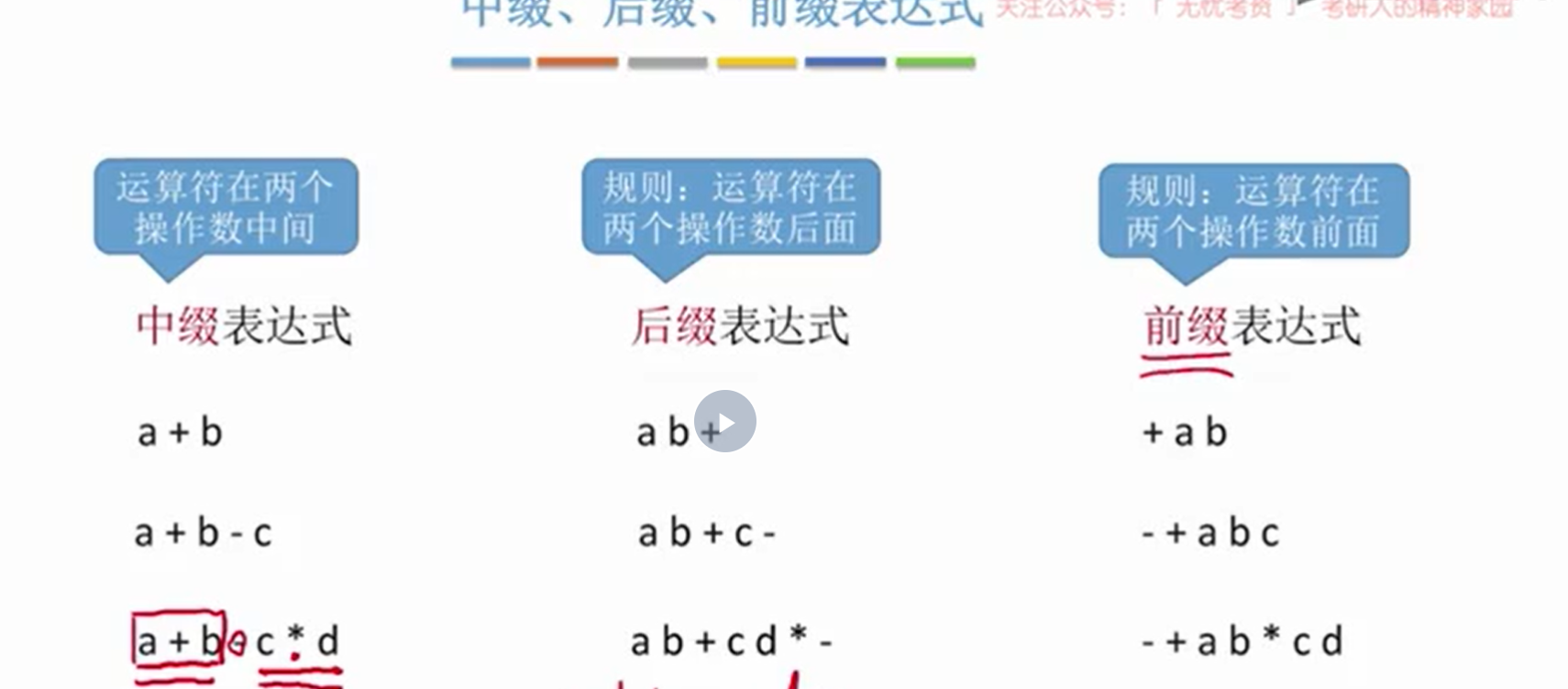
表达式求值


7. 队列
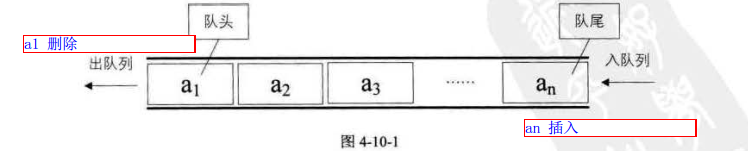
// 抽象数据类型
InitQueue(*Q); // 初始化操作,建立一个空队列
DestroyQueue(*Q); // 若队列存在则销毁它
ClearQueue(*Q); // 将队列清空
QueueEmpty(*Q); // 若队列为空返回 true
GetHead(Q,*e); // 若队列存在且非空,用 e 返回队列 Q 的队头元素
EnQueue(*Q,e); // 若队列存在,插入新元素 e 到队列 Q 中并称为队尾元素
DeQueue(*Q,*e); // 删除队列 Q 中队头元素,并用 e 返回其值
QueueLength(Q); // 返回队列 Q 中的元素个数
7.1 循环队列
队列用 front 来表示头指针,rear 来表示尾指针,当 front = rear 时,表示空队列。
note:
- front 指向刚出队的位置,rear 指向刚进队的位置,指向队尾的下一个存储空间。出队 front 后移,进队 rear 后移
出队操作 front=(front+1)%8,这样 front 的取值就在环内(0,1,2,3,4,5,6,7,0,1…)
1. 队满和队空的判断问题
队空:
front == rear- 队满,我们让数组中还有一个空闲单元表示队满(而不是全部空间被占用),如下图。

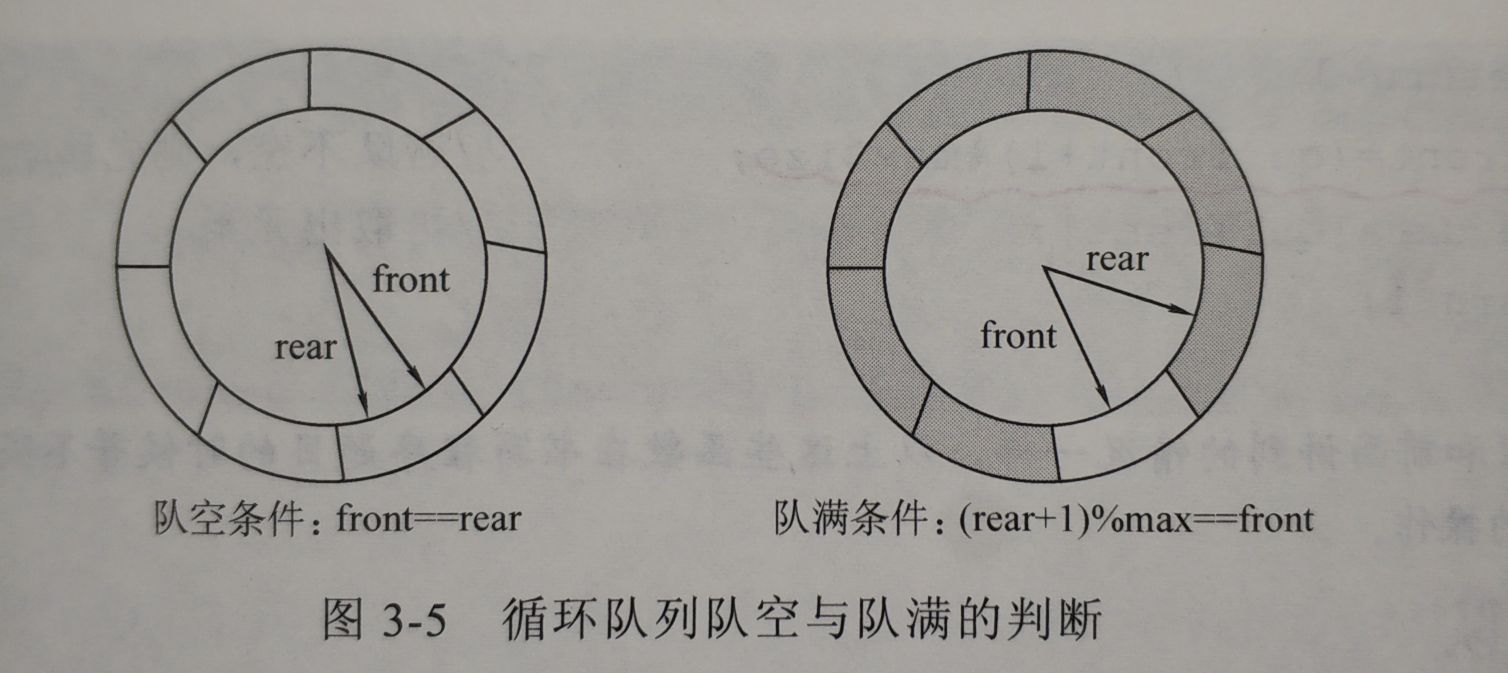
队空
front == rear;
进队和出队
出队 front = (front+1)%maxSize
进队 rear = (rear+1)%maxSize
队满判断的公式
队列长度公式
其中 QueueSize 表示队列的最大尺寸
2. 循环队列的基本操作
typedef int QElemType;
typedef int Status;
typedef struct
{
QElemType data[MAXSIZE];
int front;
int rear;
}SqQueue;
// 初始化
Status initQueue(SqQueue *Q)
{
Q->front=0;
Q->rear=0;
return 1;
}
// 返回队列的长度
Status Queuelength(SqQueue Q)
{
return (Q.rear-Q.front+MAXSIZE)%MAXSIZE;
}
//入队操作
Status EnQueue(SqQueue *Q,QElemType e)
{
if((Q->rear+1)%MAXSIZE==Q->front)
return 0;
Q->data[Q->rear]=e;
// rear 的指针向后移一位(循环后移)
Q->rear=(Q->rear+1)%MAXSIZE;
return 1;
}
// 出队操作
Status DeQueue(SqQueue *Q,QElemType *e)
{
if(Q->front==Q->rear)
return 0;
*e = Q->data[Q->front];
Q->front = (Q->front+1)%MAXSIZE;
return 1;
}
7.2 队列的链式存储结构及实现
链队列的头指针指向队列的头结点,队尾指针指向终端结点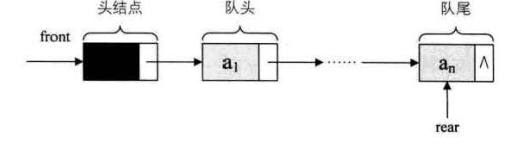
- 链队没有队满的情况,因为是链,所以只要内存不满就不满
- 其中链尾作为队尾,链头作为队头
1 抽象数据结构
typedef int QElemType;
typedef struct QNode
{
QElemType data;
struct QNode *next;
}QNode,*QueuePtr;
typedef struct
{
QueuePtr font,rear;
}LinkQueue;
判空的条件
// 两个任何一个满足则满足链队空的条件
lqu->rear == NULL;
lqu->first == NULL;
7.2 入队操作
在尾部插入结点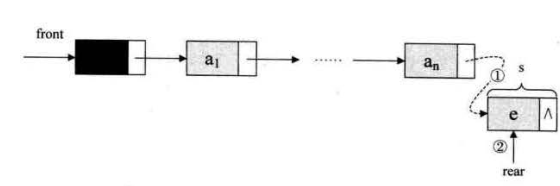
// 入队
Status EnQueue(LinkQueue *Q,QElemType e)
{
QueuePtr s=(QueuePtr)malloc(sizeof(QNode));
if(!s)
exit(0);
s->data=e;
s->next=NULL;
Q->rear->next=s; // 把新结点放到原队尾结点的后继
Q->rear=s; // 把 s 结点正式设为队尾结点
return 1;
}
7.3 出队操作
- 将头结点的后继改为它后面的结点,若只剩一个元素,则将 rear 指向头结点
- 对于出队操作,可能会首尾两个节点都要修改
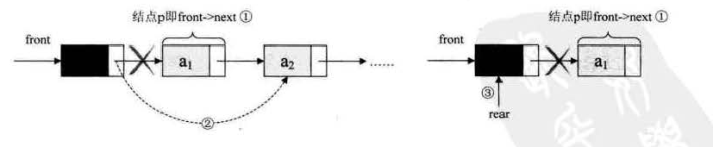
// 出队
Status DeQueue(LinkQueue *Q,QElemType *e)
{
QueuePtr p;
if(Q->front==Q->rear)
return 0;
p=Q->front->next;
*e=p->data;
Q->front->next=p->next;
if(Q->rear==p)
Q->rear=Q->front;
free(p);
return 1;
}
7.4 双端队列
见《天勤高分笔记》
7.5 链队
1. 链队的实现(定义)
2. 链队的初始化(带头结点)

4. 入队(带头结点)
![H~6[[XOBL8%2F881P9IX4]X.png](/uploads/projects/fromdark@yx0hps/ea40854302d6b91df82dab5ee9a2d0cb.png)
5. 入队(不带头结点)
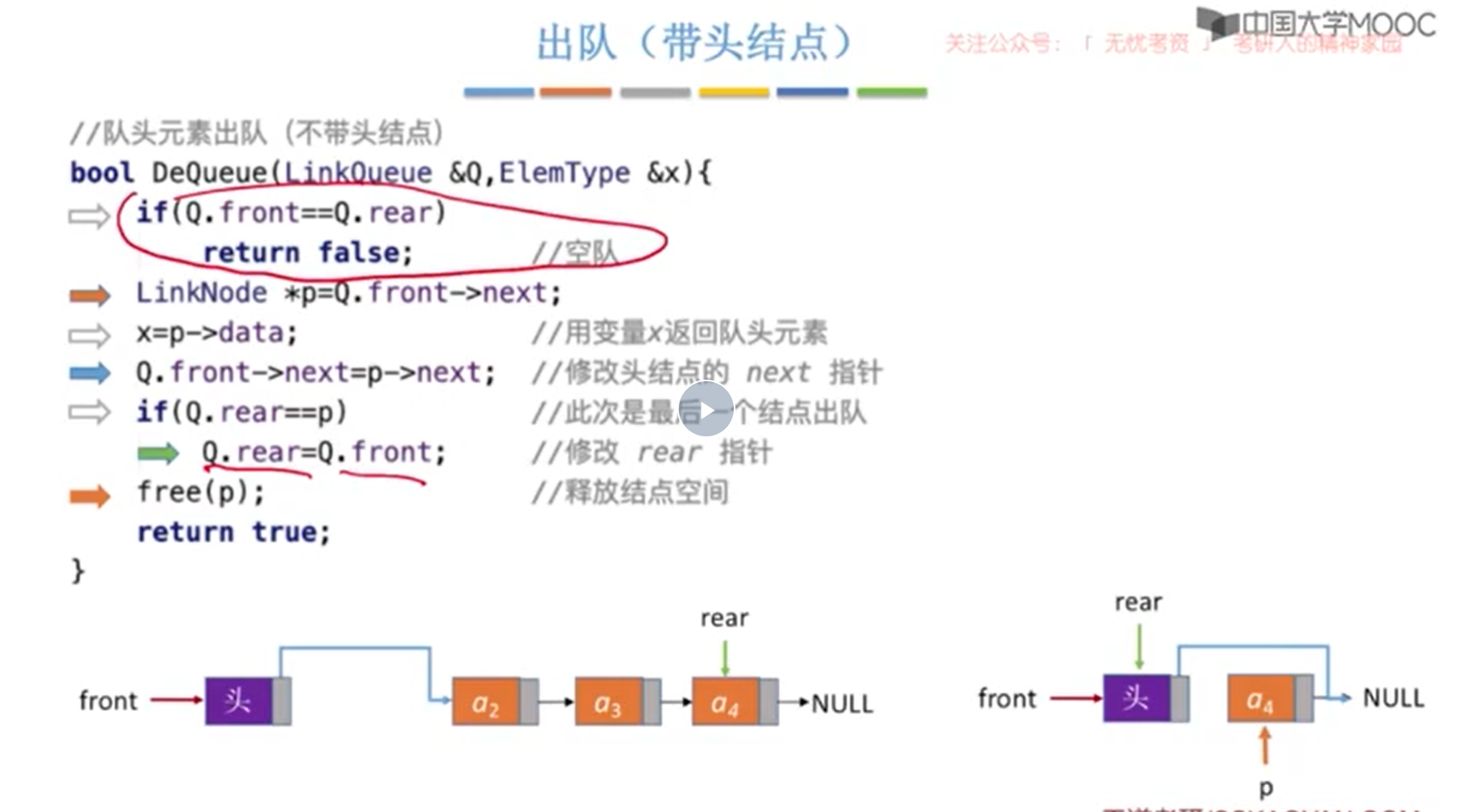
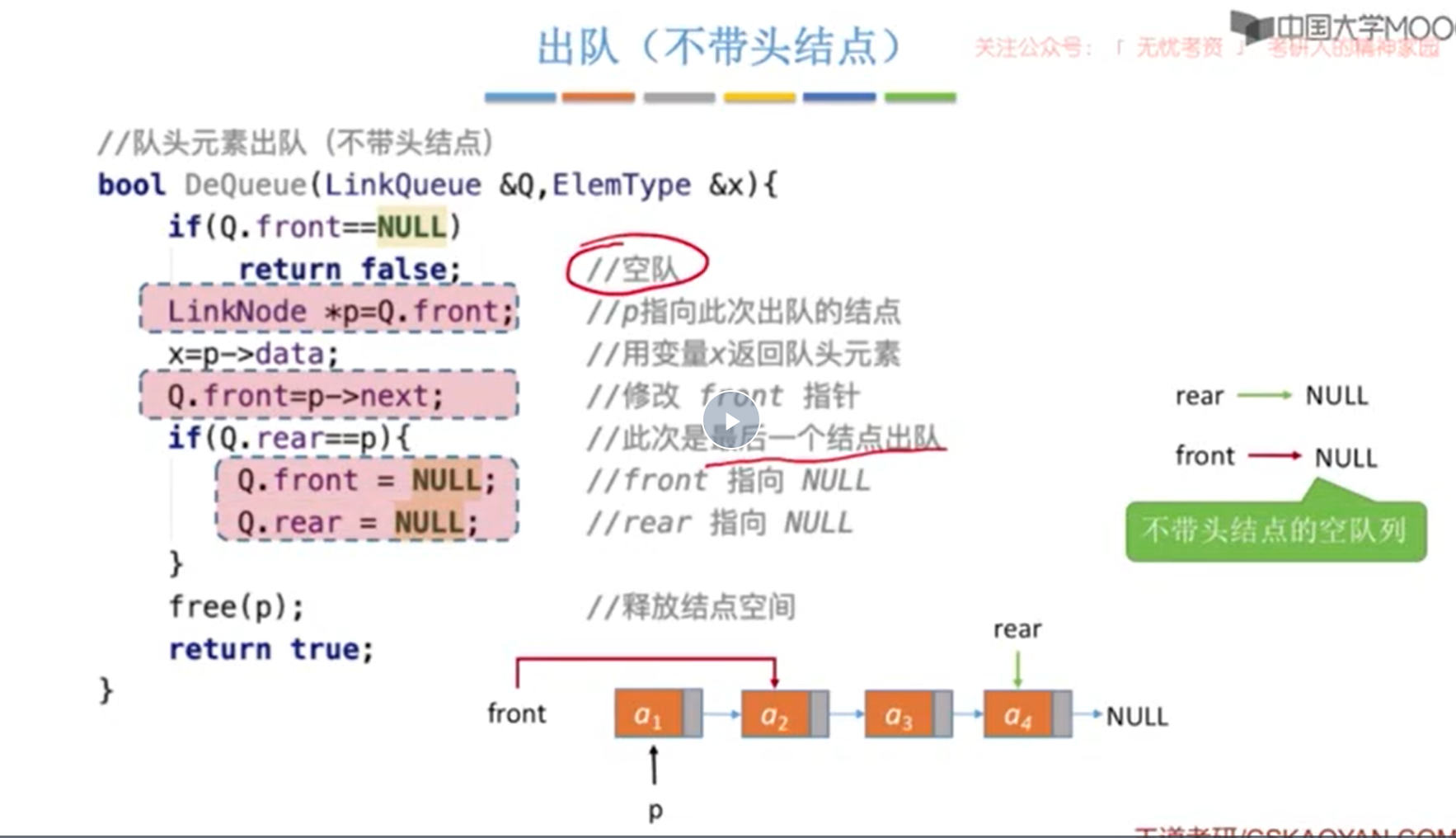
7. 出队(不带头结点)
8. 其他考点
1. 判断操作系列是否合法
- 输入操作个数 = 输出操作个数
- 在给定范围内,输入操作个数 > 输出操作个数
- 出栈数量有多少![%%TI60{04_8~NK)NLH8BNO.png
![OQ[S(84CZC]U2V68T8RQMP6.png](/uploads/projects/fromdark@yx0hps/6ec03a225350da46ff176e3d0e5d2348.png)
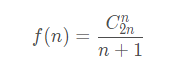
![0B0X4L8W_MUA{8A7HAB]U%V.png](/uploads/projects/fromdark@yx0hps/8dfca4518064b62e6c50c8ceb2d2f603.png)

