LRU力扣地址:https://leetcode-cn.com/problems/lru-cache/
题目要求:
运用你所掌握的数据结构,设计和实现一个 LRU (最近最少使用) 缓存机制 。实现 LRUCache 类:1、LRUCache(int capacity) 以正整数作为容量 capacity 初始化 LRU 缓存2、int get(int key) 如果关键字 key 存在于缓存中,则返回关键字的值,否则返回 -1 。3、void put(int key, int value) 如果关键字已经存在,则变更其数据值;如果关键字不存在,则插入该组「关键字-值」。当缓存容量达到上限时,它应该在写入新数据之前删除最久未使用的数据值,从而为新的数据值留出空间。来源:力扣(LeetCode)链接:https://leetcode-cn.com/problems/lru-cache著作权归领扣网络所有。商业转载请联系官方授权,非商业转载请注明出处。
解法一:使用自定义单链表的形式进行实现
自定义的单链表缓存对于第21个用例无法通过,会超出时间限制,就先放过吧,哈哈,虽然有点笨,写的还慢。
package 极客算法.基础38讲._01_LRU缓存算法;/*** 思路:使用单链表的形式进行控制LRU缓存淘汰算法* 解题思路:* 1.使用链表的方式来实现,LRU缓存淘汰策略* 2.对于get与put操作* get操作:(1)如果关键字 key 存在于缓存中,则返回关键字的值,否则返回 -1 。* put操作:(1)如果关键字已经存在,则变更其数据值;* (2)如果关键字不存在,则插入该组「关键字-值」。* (3)当缓存容量达到上限时,它应该在写入新数据之前删除最久未使用的数据值,从而为新的数据值留出空间。* 来源:力扣(LeetCode)* 链接:https://leetcode-cn.com/problems/lru-cache* 著作权归领扣网络所有。商业转载请联系官方授权,非商业转载请注明出处。* ["LRUCache","put","put","get","put","get","put","get","get","get"]* [[2],[1,1],[2,2],[1],[3,3],[2],[4,4],[1],[3],[4]]** LRUCache lRUCache = new LRUCache(2);* lRUCache.put(1, 1); // 缓存是 {1=1}* lRUCache.put(2, 2); // 缓存是 {1=1, 2=2}* lRUCache.get(1); // 返回 1* lRUCache.put(3, 3); // 该操作会使得关键字 2 作废,缓存是 {1=1, 3=3}* lRUCache.get(2); // 返回 -1 (未找到)* lRUCache.put(4, 4); // 该操作会使得关键字 1 作废,缓存是 {4=4, 3=3}* lRUCache.get(1); // 返回 -1 (未找到)* lRUCache.get(3); // 返回 3* lRUCache.get(4); // 返回 4** 来源:力扣(LeetCode)* 链接:https://leetcode-cn.com/problems/lru-cache* 著作权归领扣网络所有。商业转载请联系官方授权,非商业转载请注明出处。*//*** Your LRUCache object will be instantiated and called as such:* LRUCache obj = new LRUCache(capacity);* int param_1 = obj.get(key);* obj.put(key,value);*//*** 1.需要声明一个单链表* 2.在一步骤之前需要一个节点的声明,* 3.为单链表进行添加相关的缓存操作*/public class MySingletonList {/*** 声明到该类MySingletonList的内部,防止和外部的LRUCache类中的Node发生冲突。* 因为在LRUCache中的Node类是声明在其同一个包下,所以会发生冲突,等于是在同一个包下存在着两个相同的类*/class Node{int key;int val;Node next;public Node(int key, int val) {this.key = key;this.val = val;}// 不用提供属性的get和set方法}/*** 单链表。里面包含些许方法,比如说* 从* {1=1, 2=2}* {2=2, 1=1}* {1=1, 3=3}* 可以看出,每次的节点的访问都是放入到链表的最后面,所以需要链表的尾节点添加操作。* 方法:(1)尾部节点的添加操作* (2)如果节点存在的话,需要进行删除。*/class LinkedList {int count; // 存储已经存在多少个节点Node head; //该节点是头节点,固定链表的节点,可以顺利找到节点的首个有用的节点public LinkedList() {head = new Node(0,0);}@Deprecatedpublic void addOld(Node newNode) {Node a = head.next;while(a!=null) {a = a.next;}// The value newNode assigned to 'a' is never useda = newNode; // 直接赋值是因为已经找到了链表的最后一个节点,所以即a节点表示的是last.next,所以可以直接赋值。++count;}public void add(Node newNode) {Node a = head;while(a.next!=null) {a = a.next;}a.next = newNode; // 直接赋值是因为已经找到了链表的最后一个节点,所以即a节点表示的是last.next,所以可以直接赋值。++count;}/*** 说明,key的值是唯一的,并且如果后面value的值默认是必须要和之前的相同的key是一样的。* @param key 通过key判断是否存在节点。* @return 返回是否存在该key值的节点,存在返回value的值,不存在返回-1,通过返回值判断exist*/public int existNode(int key) {Node a = head.next;while(a!=null) {if(a.key == key) return a.val;a = a.next;}// 当前节点a指向了最后一个元素。return -1;}/*** 因为是作为缓存使用,所以不存在单独删除节点的存在。* 一般使用都是,因为该节点已经存在于缓存当中,但是在链表中需要移动到最后一个元素。所以需要进行删除* @param key*/public void delNode(int key) {Node a = head; // 作为需要删除节点的前一个节点进行使用Node b = head.next;while (b != null) {if(b.key == key) {// 对于删除操作,应该是已经确认了已经存在该节点,所以才进行删除操作。a.next = b.next;--count;return ;} else {// 节点向后移动a = b;b = a.next;}}}/*** 删除头节点,最近未使用的*/public void delFirstNode1() {Node a = head;a = a.next;--count;}/*** 删除头节点,最近未使用的*/public void delFirstNode() {Node a = head;a.next = a.next.next;--count;}public String toString() {Node a = head.next;String str = new String();System.out.println(this.count);while(a!=null) {str = a.key + "," + a.val;a = a.next;}return "{" + str + "}";}}int capacity;LinkedList linkedList;public MySingletonList(int capacity) {this.capacity = capacity;linkedList = new LinkedList();}@Deprecatedpublic int get1(int key) {return linkedList.existNode(key);}/*** 这里需要先将Node查找到的进行删除再添加。* @param key* @return*/public int get(int key) {int result = linkedList.existNode(key);if(result == -1) {return result;}linkedList.delNode(key);linkedList.add(new Node(key, result));return result;}/*** 进行put操作的话,首先需要先进行链表判断是否存在该节点* 存在的话,进行删除和添加操作* 不存在的话,进行删除,在进行添加操作* @param key* @param value*/public void put(int key, int value) { // 这里需要进行优化,否者再力扣中会超出时间限制int result = linkedList.existNode(key);if(result==-1) {// 不存在,进行判断缓存是否已经满了。if(this.capacity == linkedList.count) { //满了,先删除头节点,再添加linkedList.delFirstNode();linkedList.add(new Node(key, value));} else { // 直接添加linkedList.add(new Node(key, value));}} else {// 存在的话,不用判断是否已经满了。linkedList.delNode(key);linkedList.add(new Node(key, value));}}// 进行测试public static void main(String[] args) {MySingletonList lRUCache = new MySingletonList(2);lRUCache.put(1, 1); // 缓存是 {1=1}lRUCache.put(2, 2); // 缓存是 {1=1, 2=2}lRUCache.get(1); // 返回 1lRUCache.put(3, 3); // 该操作会使得关键字 2 作废,缓存是 {1=1, 3=3}lRUCache.put(4, 4); // 该操作会使得关键字 1 作废,缓存是 {4=4, 3=3}lRUCache.get(1); // 返回 -1 (未找到)lRUCache.get(3); // 返回 3lRUCache.get(4); // 返回 4}}
解法二:双向链表+hash表
https://leetcode-cn.com/problems/lru-cache/solution/zui-jin-mian-zi-jie-yi-mian-peng-dao-lia-1t15/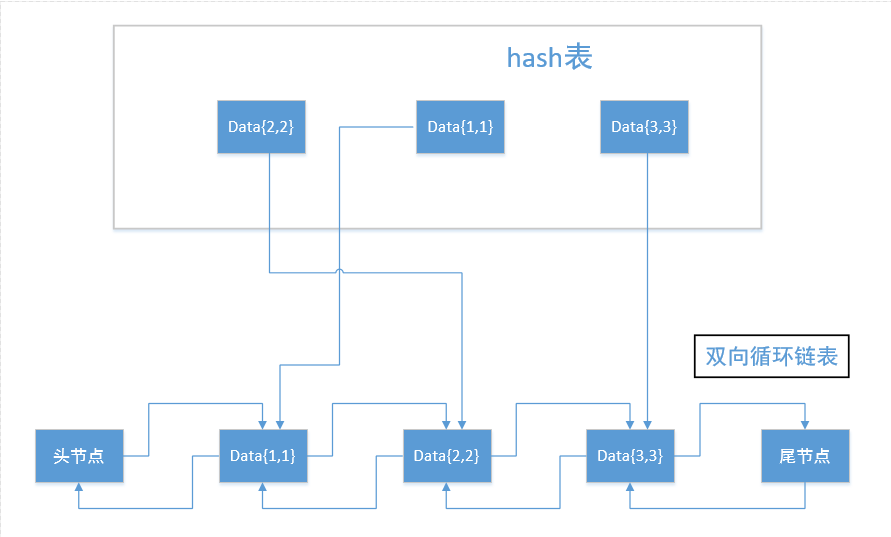
package 极客算法.基础38讲._01_LRU缓存算法;
import java.util.HashMap;
/**
* 采用hash表+双向链表的方式进行实现LRUChche缓存策略
* 双向链表相对于单链表而言,删除更加快速。并且通过Hash表的存储方式,能够将Node的查询速度加快。
* 并且对于传入的key和value值而言,key是唯一的,并且只有唯一的value,这是一个默认就是已经存在的标准
*/
public class DoubleLinkedListAndHashTable {
/**
* HashMap只能放到外面,因为是采用双向循环链表+Hash表的组合的方式进行处理。所以不能再双向链表中包含Hash表。
* 之前一直再写的时候并没有特别去关心数据结构所放到的位置,导致许多地方无从下手,通过对视频的观看学习,发现保持头脑清醒和
* 清晰的解题思路才是正确的,否则一直会在困难螺旋中一直出不来。
*/
HashMap<Integer, Node> hash;
DoubleLinkedList doubleLinkedList;
int capacity;
public DoubleLinkedListAndHashTable(int capacity) {
this.capacity = capacity;
hash = new HashMap<>();
doubleLinkedList = new DoubleLinkedList();
}
public int get(int key) {
if(hash.containsKey(key)) {
// 注意这里还有一个隐藏的操作就是查询到的时候,需要将双向链表中的节点删除再添加
// 此时双向链表是一定存在的。
// int value = doubleLinkedList.delNode(hash.get(key)); // 这个和下面这个也是可以的。因为每次put都会创建新的节点
int value = hash.get(key).val;
put(key, value);
return value;
}
return -1;
}
public void put(int key, int value) {
// 先判断是否存在。
if(hash.containsKey(key)) {
//存在的话,先删除再添加
Node node = new Node(key, value);
this.doubleLinkedList.delNode(hash.get(key));
this.doubleLinkedList.addFirstNode(node);
hash.put(key,node);
} else {
// 不存在的话,先要进行判断缓存是否已经满了
Node newNode = new Node(key, value);
if(hash.size() == capacity) {
// 先删除头节点。再添加
int key2 = doubleLinkedList.delLastNode();
hash.remove(key2);
doubleLinkedList.addFirstNode(newNode);
} else {
// 没有满的话直接添加到两个地方
doubleLinkedList.addFirstNode(newNode);
}
hash.put(key, newNode);
}
}
/**
* 双向链表需要提供的操作:
* 首先先从单链表去看,我们完成需要哪些功能,再近似成功的写法上完成类似的功能。
* 1)判断是否存在该节点
* 2)插入节点(尾插)
* 3)删除节点
*
* 对于上面的三个方法,我们需要实现的方法主要是插入和删除,因为Hash表会为我们提供某些方法
* 比如说通过HashMap<Integer, Node>的方式通过查询key的存在可以判断节点的存在。
* 另外Hash表里面有获得表的存储的节点的大小的方法。
* 综上所叙述,我们双向链表只需要实现两个方法即可。尾部插入和删除操作
*/
class DoubleLinkedList {
Node head;
Node tail; // tail 尾巴
public DoubleLinkedList() {
head = new Node(0,0);
tail = new Node(0,0);
// 这里必须要在初始化的时候进行连接上,否则会报空指针异常
head.next = tail;
tail.prev = head;
}
/**
* 节点操作最好对应节点操作。。。
* @param key
*/
@Deprecated
public void delNode1(int key) {
Node first = head.next;
while(first.key != key) {
first = first.next;
}
// 进行节点的删除。
Node prev = first.prev;
Node next = first.next;
prev.next = next;
next.prev = prev;
}
public int delNode(Node node) {
// 此时的节点已经是在链表中的节点,所以直接将其当为链表中的节点进行操作
node.prev.next = node.next;
node.next.prev = node.prev;
return node.val;
}
public void addFirstNode(Node newNode) {
newNode.next = head.next;
newNode.prev = head;
head.next.prev = newNode;
head.next = newNode;
}
public int delLastNode() {
Node last = tail.prev;
last.prev.next = tail;
tail.prev = last.prev;
return last.key;
}
}
class Node {
int key;
int val;
Node next; // 表示下一个节点
Node prev; // 表示指向前一个节点
public Node(int key, int val) {
this.key = key;
this.val = val;
}
}
}
解法三:力扣官方



一看到键和值就想到hash表,因为其可以得到O(1)的复杂度
因为要每次get的时候都是需要更新数据的
package 极客算法.基础38讲._01_LRU缓存算法;
import java.util.HashMap;
import java.util.Map;
public class OfficialSolutionLRUCache {
class DLinkedNode {
int key;
int value;
DLinkedNode prev;
DLinkedNode next;
public DLinkedNode() { // 这样感觉后面写感觉舒服些。对吧。。。
}
public DLinkedNode(int _key, int _value) {
key = _key;
value = _value;
}
}
private Map<Integer, DLinkedNode> cache = new HashMap<Integer, DLinkedNode>();
private int size;
private int capacity;
private DLinkedNode head, tail;
public OfficialSolutionLRUCache(int capacity) {
this.size = 0;
this.capacity = capacity;
// 使用伪头部和伪尾部节点
head = new DLinkedNode();
tail = new DLinkedNode();
head.next = tail;
tail.prev = head;
}
public int get(int key) {
DLinkedNode node = cache.get(key);
if (node == null) {
return -1;
}
// 如果 key 存在,先通过哈希表定位,再移到头部
moveToHead(node);
return node.value;
}
public void put(int key, int value) {
DLinkedNode node = cache.get(key);
if (node == null) {
// 如果 key 不存在,创建一个新的节点
DLinkedNode newNode = new DLinkedNode(key, value);
// 添加进哈希表
cache.put(key, newNode);
// 添加至双向链表的头部
addToHead(newNode);
++size; //?这样是为了,提高效率吗。
if (size > capacity) {
// 如果超出容量,删除双向链表的尾部节点
DLinkedNode tail = removeTail();
// 删除哈希表中对应的项
cache.remove(tail.key);
--size;
}
}
else {
// 如果 key 存在,先通过哈希表定位,再修改 value,并移到头部
node.value = value;
moveToHead(node);
}
}
private void addToHead(DLinkedNode node) {
node.prev = head;
node.next = head.next;
head.next.prev = node;
head.next = node;
}
private void removeNode(DLinkedNode node) {
node.prev.next = node.next;
node.next.prev = node.prev;
}
// node一定是被前后节点所包围的。无需担心,正常使用
private void moveToHead(DLinkedNode node) {
removeNode(node);
addToHead(node);
}
private DLinkedNode removeTail() {
DLinkedNode res = tail.prev;
removeNode(res);
return res;
}
}
//
// 作者:LeetCode-Solution
// 链接:https://leetcode-cn.com/problems/lru-cache/solution/lruhuan-cun-ji-zhi-by-leetcode-solution/
// 来源:力扣(LeetCode)
// 著作权归作者所有。商业转载请联系作者获得授权,非商业转载请注明出处。

