借助递归树来分析递归算法的时间复杂度。

递归树与时间复杂度分析

递归的思想就是，将大问题分解为小问题来求解，然后再将小问题分解为小小问题。
如果我们把这个一层一层的分解过程画成图，它其实就是一棵树。我们给这棵树起一个名字，叫作递归树。
斐波那契递归树：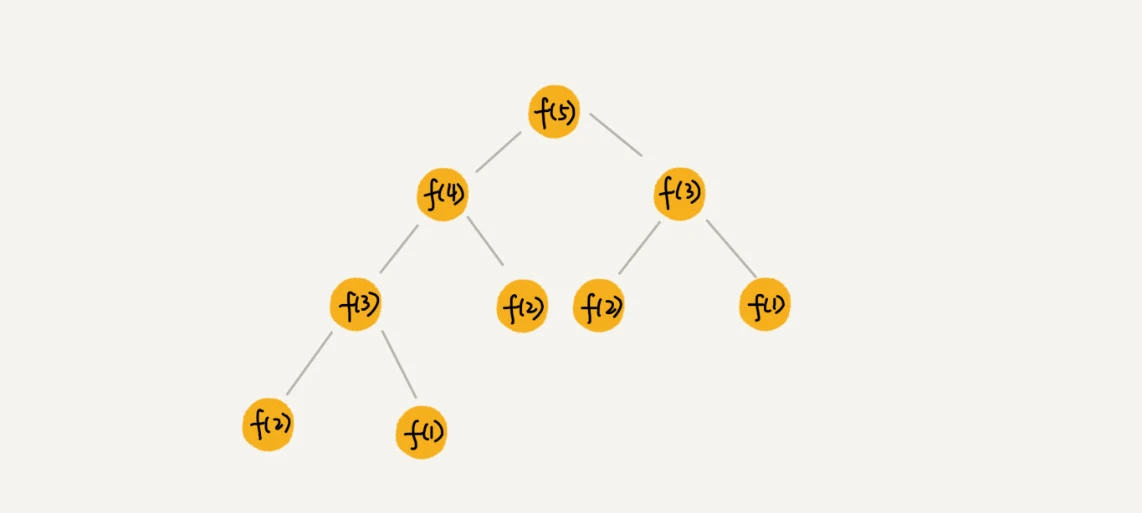

归并排序：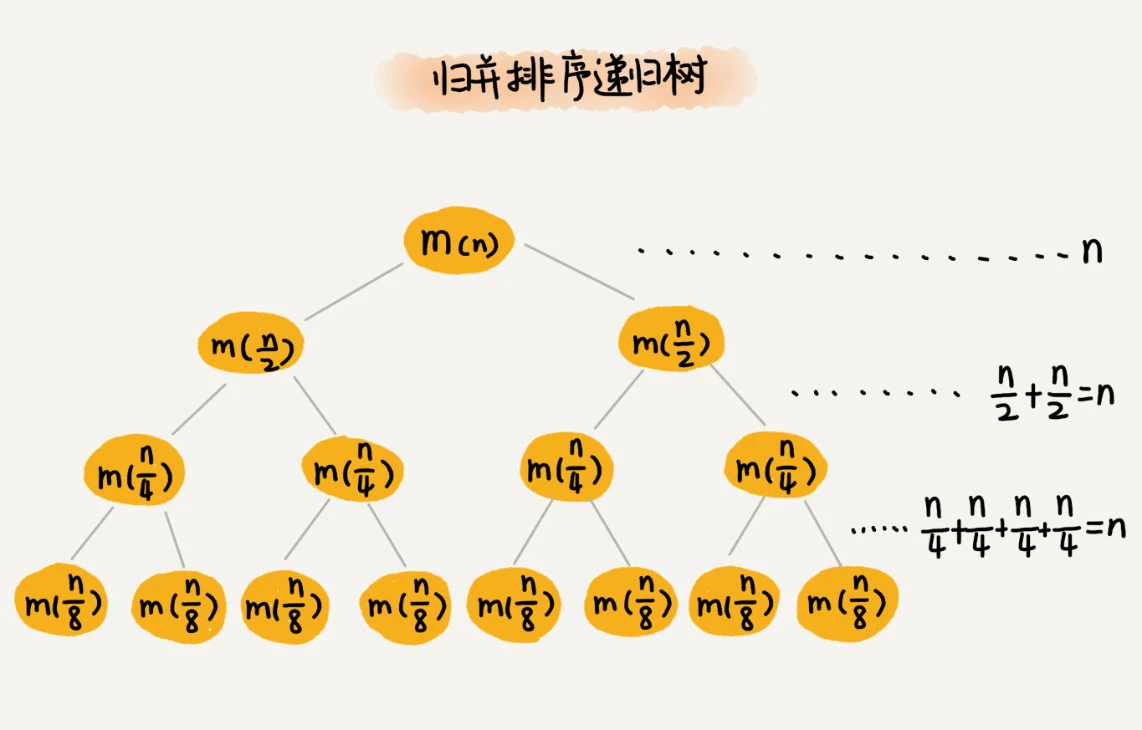

因为每次分解都是一分为二，所以代价很低，我们把时间上的消耗记作常量 1。归并算法中比较耗时的是归并操作，也就是把两个子数组合并为大数组。从图中我们可以看出，每一层归并操作消耗的时间总和是一样的，跟要排序的数据规模有关。我们把每一层归并操作消耗的时间记作 n。
现在，我们只需要知道这棵树的高度 h，用高度 h 乘以每一层的时间消耗 n，就可以得到总的时间复杂度 O(n∗h)。
从归并排序的原理和递归树，可以看出来，归并排序递归树是一棵满二叉树。我们前两节中讲到，满二叉树的高度大约是 log2n，所以，归并排序递归实现的时间复杂度就是 O(nlogn)。我这里的时间复杂度都是估算的，对树的高度的计算也没有那么精确，但是这并不影响复杂度的计算结果。

实战一：分析快速排序的时间复杂度

在用递归树推导之前，我们先来回忆一下用递推公式的分析方法。你可以回想一下，当时，我们为什么说用递推公式来求解平均时间复杂度非常复杂？
快速排序在最好情况下，每次分区都能一分为二，这个时候用递推公式 T(n)=2T(n/2 )+n，很容易就能推导出时间复杂度是 O(nlogn)。但是，我们并不可能每次分区都这么幸运，正好一分为二。
我们假设平均情况下，每次分区之后，两个分区的大小比例为 1:k。当 k=9 时，如果用递推公式的方法来求解时间复杂度的话，递推公式就写成 T(n)=T(n/10)+T(9n/10)+n。
这个公式可以推导出时间复杂度，但是推导过程非常复杂。那我们来看看，用递归树来分析快速排序的平均情况时间复杂度，是不是比较简单呢？我们还是取 k 等于 9，也就是说，每次分区都很不平均，一个分区是另一个分区的 9 倍。如果我们把递归分解的过程画成递归树，就是下面这个样子：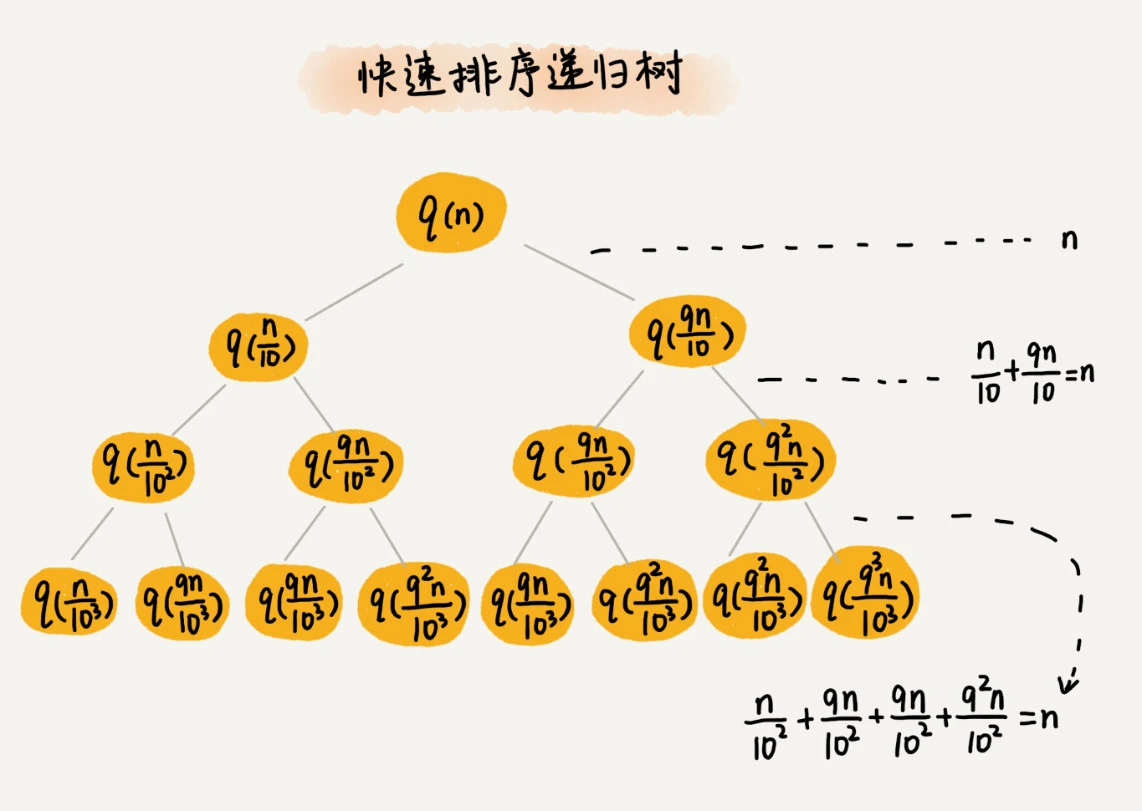

快速排序的过程中，每次分区都要遍历待分区区间的所有数据，所以，每一层分区操作所遍历的数据的个数之和就是 n。我们现在只要求出递归树的高度 h，这个快排过程遍历的数据个数就是 h∗n ，也就是说，时间复杂度就是 O(h∗n)。
因为每次分区并不是均匀地一分为二，所以递归树并不是满二叉树。这样一个递归树的高度是多少呢？
我们知道，快速排序结束的条件就是待排序的小区间，大小为 1，也就是说叶子节点里的数据规模是 1。从根节点 n 到叶子节点 1，递归树中最短的一个路径每次都乘以 1/10，最长的一个路径每次都乘以 9/10。通过计算，我们可以得到，从根节点到叶子节点的最短路径是 (log10)n，最长的路径是 (log10/9)n。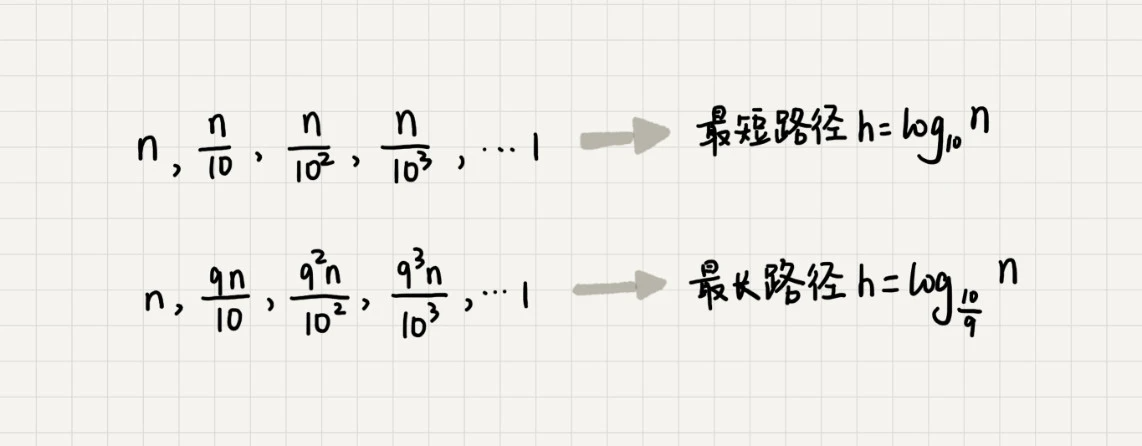

所以，遍历数据的个数总和就介于 n(log10)n 和 n(log10/9)n 之间。根据复杂度的大 O 表示法，对数复杂度的底数不管是多少，我们统一写成 logn，所以，当分区大小比例是 1:9 时，快速排序的时间复杂度仍然是 O(nlogn)。
刚刚我们假设 k=9，那如果 k=99，也就是说，每次分区极其不平均，两个区间大小是 1:99，这个时候的时间复杂度是多少呢？
我们可以类比上面 k=9 的分析过程。当 k=99 的时候，树的最短路径就是 (log100)n，最长路径是 (log100/99)n，所以总遍历数据个数介于 n(log100)n 和 n(log100/99)n之间。尽管底数变了，但是时间复杂度也仍然是 O(nlogn)。
也就是说，对于 k 等于 9，99，甚至是 999，9999……，只要 k 的值不随 n 变化，是一个事先确定的常量，那快排的时间复杂度就是 O(nlogn)。所以，从概率论的角度来说，快排的平均时间复杂度就是 O(nlogn)。

实战二：分析斐波那契数列的时间复杂度

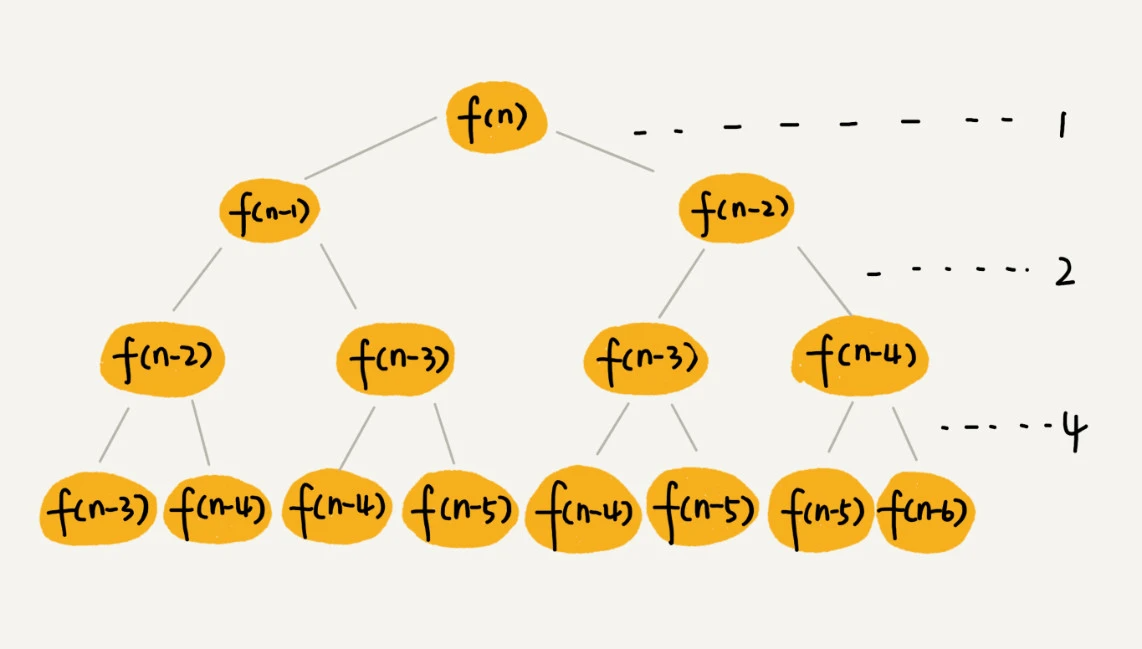
这棵递归树的高度是多少呢？
f(n) 分解为 f(n−1) 和 f(n−2)，每次数据规模都是 −1 或者 −2，叶子节点的数据规模是 1 或者 2。所以，从根节点走到叶子节点，每条路径是长短不一的。如果每次都是 −1，那最长路径大约就是 n；如果每次都是 −2，那最短路径大约就是 n/2。
每次分解之后的合并操作只需要一次加法运算，我们把这次加法运算的时间消耗记作 1。所以，从上往下，第一层的总时间消耗是 1，第二层的总时间消耗是 2，第三层的总时间消耗就是 2^2。依次类推，第 k 层的时间消耗就是 2^(k−1)，那整个算法的总的时间消耗就是每一层时间消耗之和。如果路径长度都为 n，那这个总和就是 2^n−1。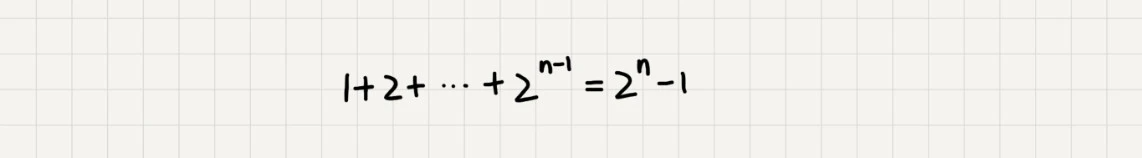

如果路径长度都是 n/2 ，那整个算法的总的时间消耗就是 2^(n/2)−1。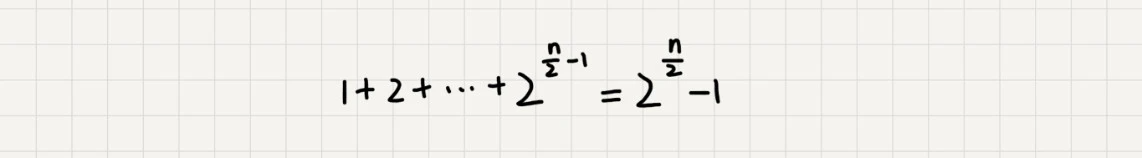

所以，这个算法的时间复杂度就介于 O(2^n) 和 O(2^(n/2)) 之间。虽然这样得到的结果还不够精确，只是一个范围，但是我们也基本上知道了上面算法的时间复杂度是指数级的，非常高。

实战三：分析全排列的时间复杂度

排列组合，n!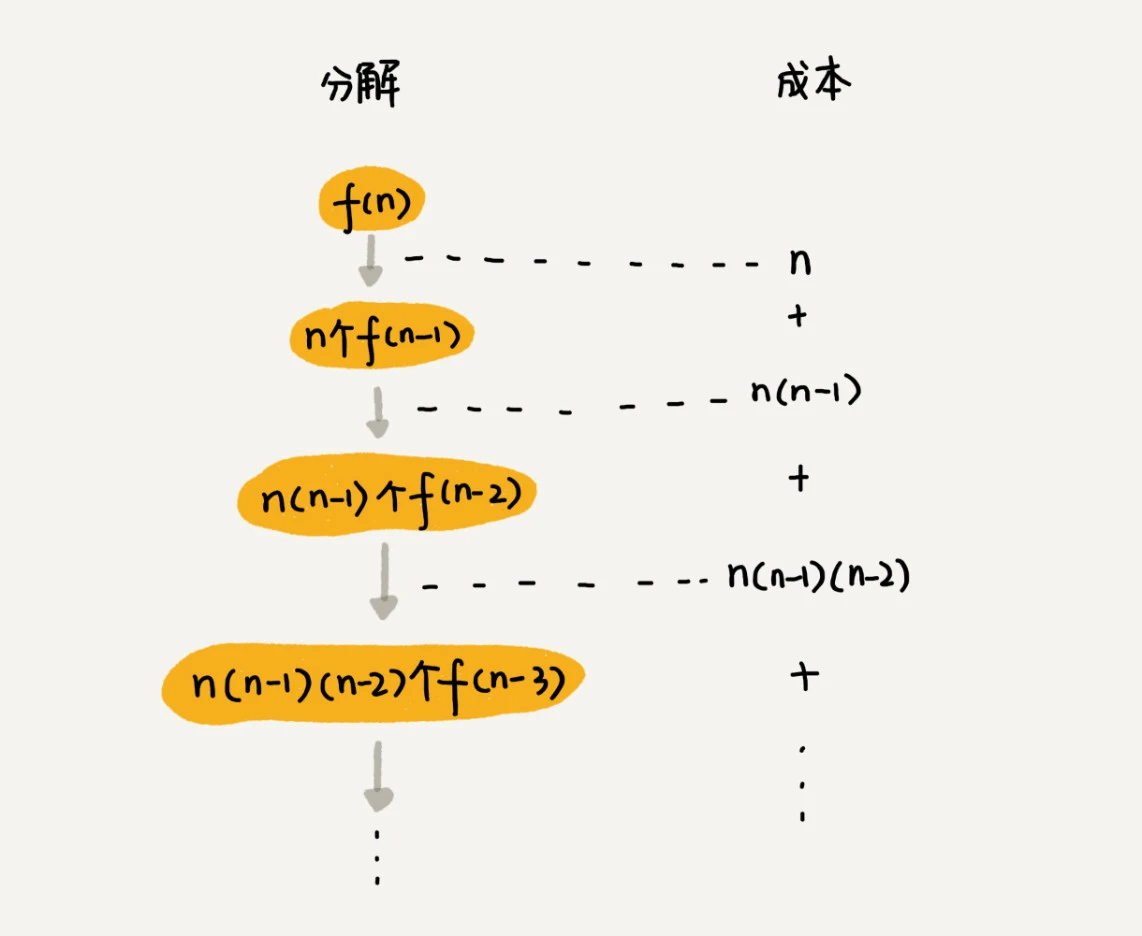

掌握分析的方法很重要，思路是重点，不要纠结于精确的时间复杂度到底是多少。

内容小结

有些代码比较适合用递推公式来分析，比如归并排序的时间复杂度、快速排序的最好情况时间复杂度；有些比较适合采用递归树来分析，比如快速排序的平均时间复杂度。而有些可能两个都不怎么适合使用，比如二叉树的递归前中后序遍历。
时间复杂度分析的理论知识并不多，也不复杂，掌握起来也不难，但是，在我们平时的工作、学习中，面对的代码千差万别，能够灵活应用学到的复杂度分析方法，来分析现有的代码，并不是件简单的事情，所以，你平时要多实战、多分析，只有这样，面对任何代码的时间复杂度分析，你才能做到游刃有余、毫不畏惧。

课后思考

1 个细胞的生命周期是 3 小时，1 小时分裂一次。求 n 小时后，容器内有多少细胞？请你用已经学过的递归时间复杂度的分析方法，分析一下这个递归问题的时间复杂度。

f(0) = 1
f(1) = f(0)2
f(2) = f(1)2
f(3) = f(2)2 - f(0)
f(4) = f(3)2 - f(1)
f(5) = f(4)2 - f(2)
f(n) = 2f(n-1) - f(n-3)

f(0) = 1
f(1) = f(0) + f(0)
f(2) = f(1) + f(1)
f(3) = f(2) + f(1) + f(0)
f(4) = f(3) + f(2) +f(1)
f(5) = f(4) + f(3) + f(2)
f(n) = f(n-1) + f(n-2)+ f(n-3)

为什么要说明第三个呢，因为这个和斐波那契类似，用加法那么就可以直接套用斐波那契的，虽然减法也可以。
那么现在就出来了
三个步长，1，2，3
那么如果步长为都为n或n/3时，那么他的区间就算出来了。
1+2+3+4…..+2^(n-1) = 2^n -1
1+4+7+…+3^(n/3-1) = 3^(n/3) -1
那么时间复杂度就介于O(2^n)到O(3^(n/3))之间。