median-of-two-sorted-arrays

中位数性质：（元素个数为n， 已排序）

  • 当 n 为奇数时，中位数是第 n/2 个元素
  • 当 n 为偶数时，中位数是第 n/2 个元素和第 n/2+1 个元素的平均值

只有1个数组时，将数组分为2个部分

  1. 当数组长度为偶数时，中位数有2个：左边数组最大值、右边数组最小值

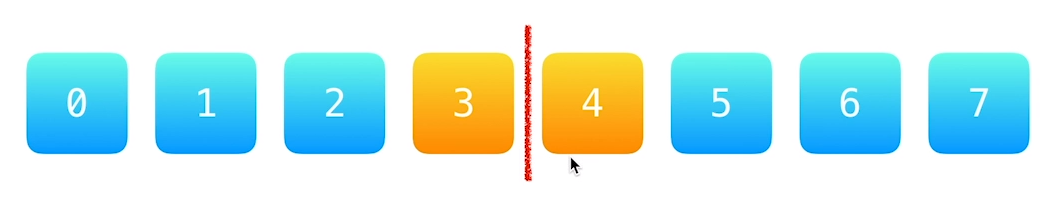
image.png

  1. 当数组为奇数时，中位数有1个，我们把中位数分到左边数组

    左边数组多一个，中位数在左边数组最大值

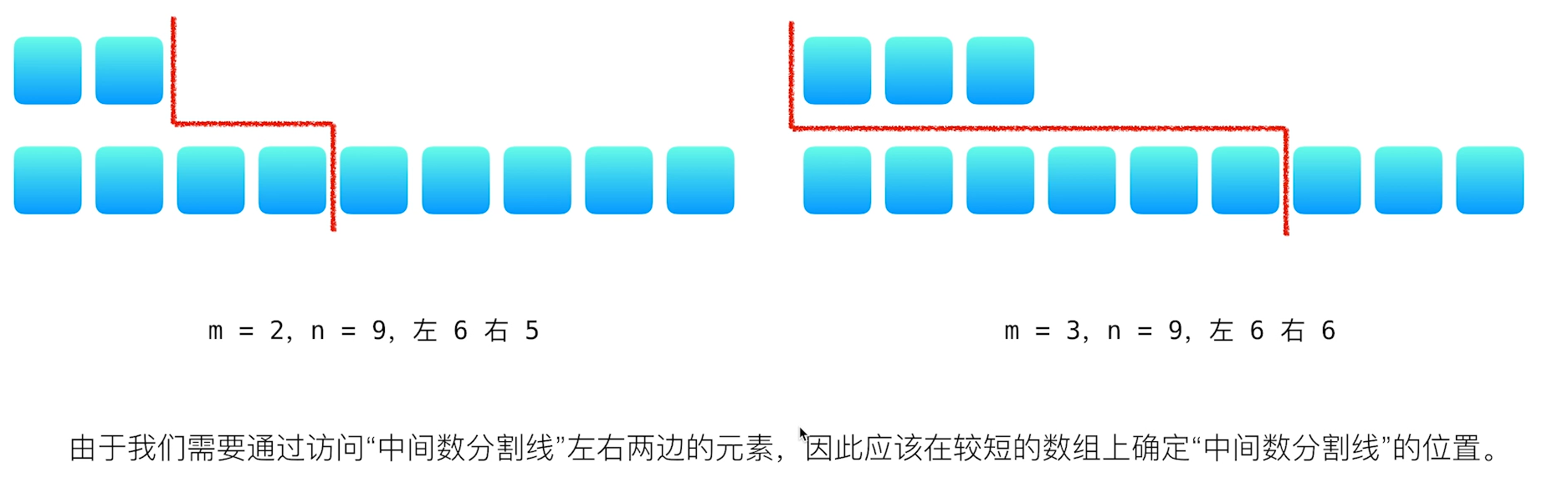
    image.png
    有2个数组时，仍可以将2个数组分割为2个部分
    image.png
    我们不用去确定分割线确定分割线在2个数组中的位置，我们计算分割线左边和右边元素的个数即可
    image.png
    要确保交叉小于等于关系
    image.png
    极端情况 1

  • 在较短的数组上确定分割线的位置，防止数组越界

image.png
极端情况 2
image.png

  1. class Solution {
  2.     public double findMedianSortedArrays(int[] nums1, int[] nums2) {
  3.         if (nums1.length > nums2.length) {
  4.             int[] tmp = nums1;
  5.             nums1 = nums2;
  6.             nums2 = tmp;
  7.         }
  8.         int m = nums1.length;
  9.         int n = nums2.length;
  10.         // 分割线左边所有元素的个数： m + (n - m + 1) /2
  11.         int totalLeft = (m + n + 1) / 2;
  13.         // 在 nums1 的区间 [0, m] 里查找恰当的分割线
  14.         // 使得 nums1[i-1] <= nums2[j] && nums2[j-1] <= nums1[i]
  15.         int left = 0;
  16.         int right = m;
  18.         // 循环条件结束的条件为指针重合，即分割线已找到
  19.         while (left < right) {
  20.             int i = left + (right - left + 1) / 2;
  21.             int j = totalLeft - i;
  22.             if (nums1[i-1] > nums2[j]) {
  23.                 // 下一轮区间为 [left, i-1]
  24.                 right = i - 1;
  25.             } else {
  26.                 // 下一轮区间为 [i, right]
  27.                 left = i;
  28.             }
  29.         }
  30.         int i = left;
  31.         int j = totalLeft -i;
  32.         int nums1LeftMax = i == 0 ? Integer.MIN_VALUE : nums1[i-1];
  33.         int nums1RightMin = i == m ? Integer.MAX_VALUE : nums1[i];
  34.         int num2LeftMax = j == 0 ? Integer.MIN_VALUE : nums2[j-1];
  35.         int num2RightMin = j == n ? Integer.MAX_VALUE : nums2[j];
  37.         if ((m + n) % 2 == 0) {
  38.             return (double) (Math.max(nums1LeftMax, num2LeftMax) + Math.min(nums1RightMin, num2RightMin)) / 2.0;
  39.         } else {
  40.             return Math.max(nums1LeftMax, num2LeftMax);
  41.         }
  43.     }
  44. }

参考：https://leetcode-cn.com/problems/median-of-two-sorted-arrays/solution/xun-zhao-liang-ge-you-xu-shu-zu-de-zhong-wei-s-114/411176