定义

红黑树是一种含有红黑节点并能自平衡的二叉树。满足以下性质

  1. 节点颜色只能是红或黑
  2. 根节点是黑色
  3. 叶子节点 NIL 是黑色
  4. 每个红色节点的2个子节点一定是黑色
  5. 任意一个节点到每个叶子节点的路径都包含数量相同的黑节点

二叉查找树

树和它的子树满足以下约束：左节点小于父节点，右节点大于父节点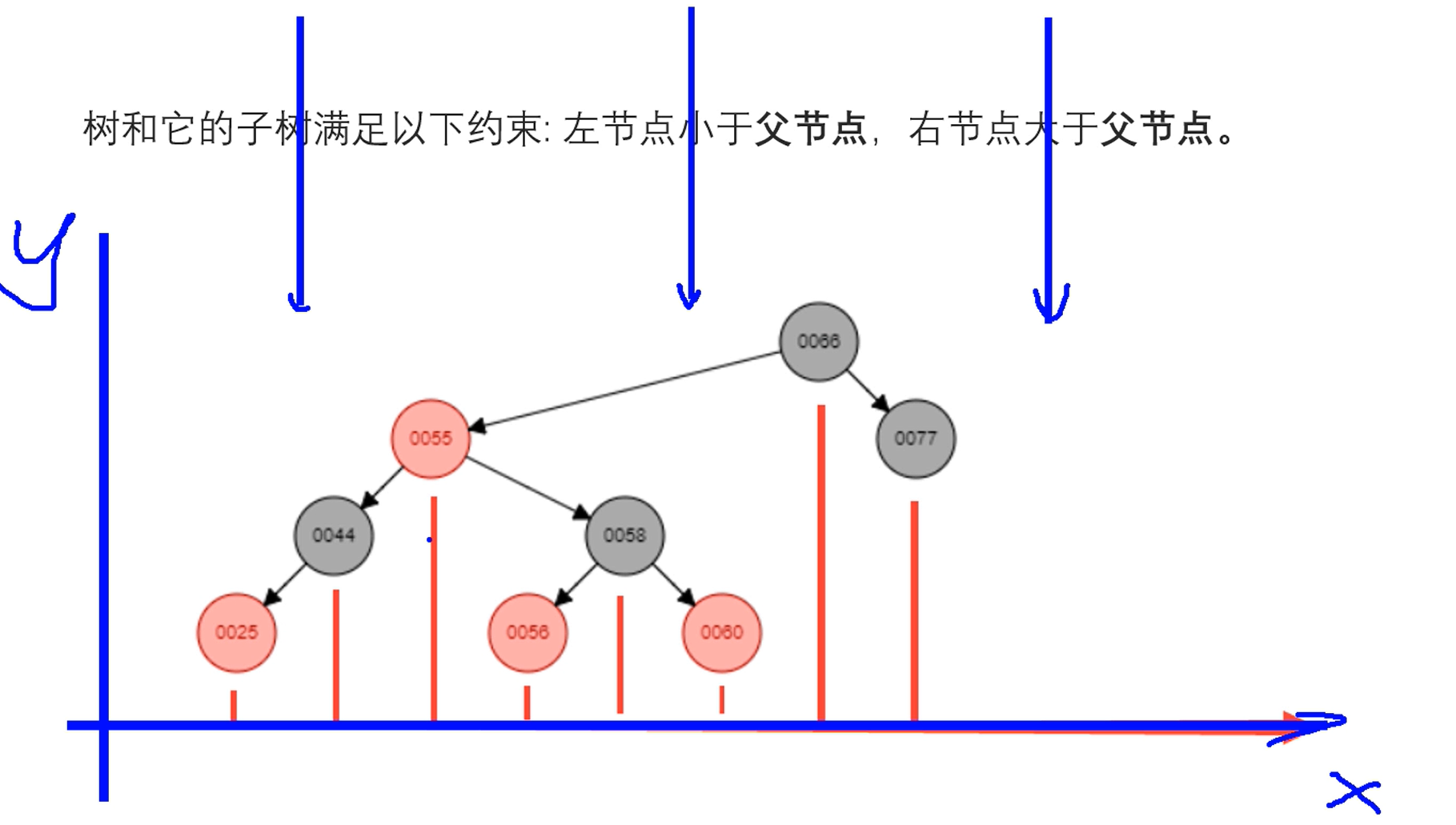
image.png

会发现投影到x轴是递增的

红黑树性质1

红黑树每个节点多了一个颜色标记位，黑色或红色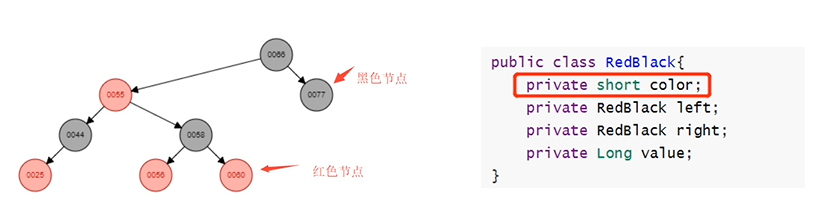
image.png

红黑树性质2

根节点是黑色的，（这样才能满足红黑树的其他性质）

红黑树性质3

每个叶子节点（NIL）都是黑色的虚拟节点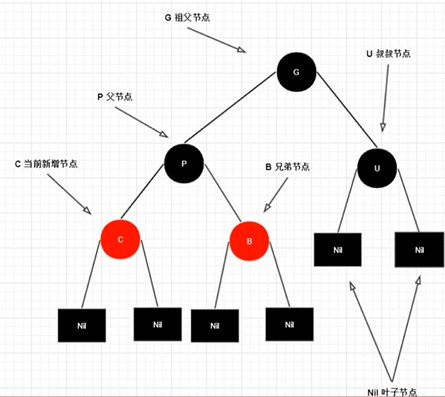
image.png

红黑树性质4

每个红色节点的两个子节点一定都是黑色
=> 不能有2个连续的红色 => 红色节点的父节点一定是黑色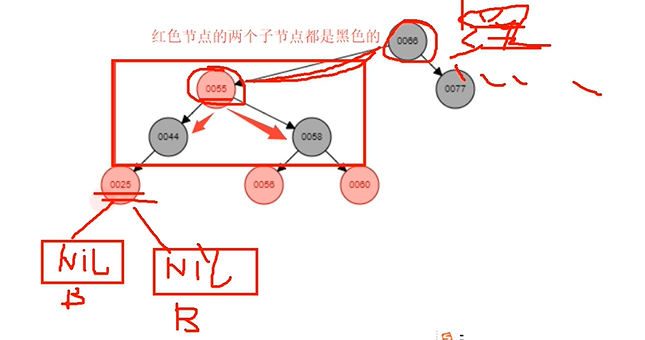
image.png

红黑树性质5

任意一节点到每个叶子节点的路径都包含数量相等的黑节点。黑色完美平衡。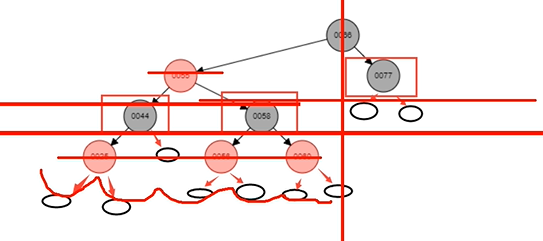
image.png

操作

红黑树的平衡性

红黑树是非完美平衡二叉树，是完美黑色平衡二叉查找树

  • 二叉查找树是一颗不稳定的树，如下图（已经变成了一个链表了）

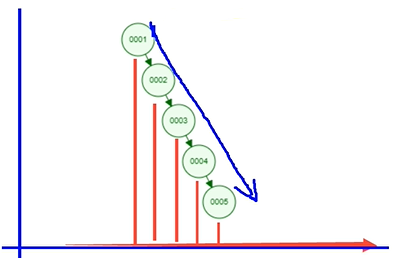
image.png

  • 红黑树是一颗稳定的平衡二叉树

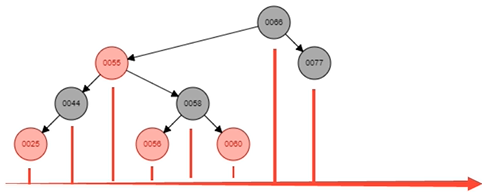
image.png

自平衡的最小单元

红黑树自平衡只考虑CPGU三代

  • C : 当前节点
  • P : 父节点
  • G : 祖父节点
  • U : 叔叔节点

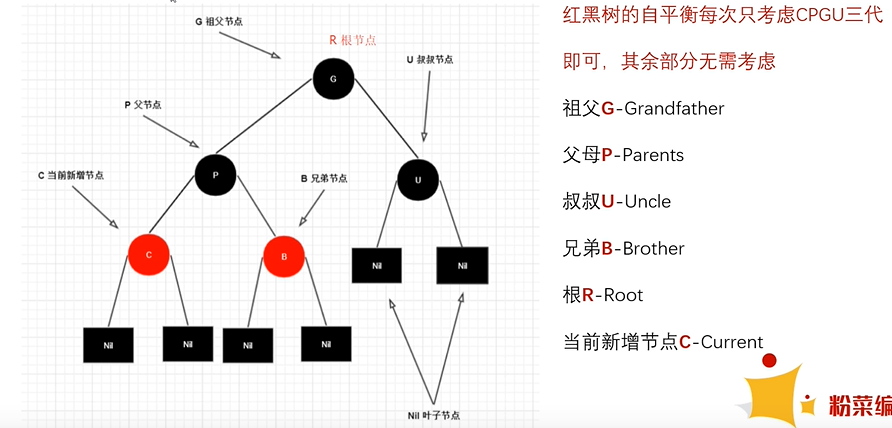
image.png

红黑树新增节点默认都是红色节点，因为红色节点它不会影响黑色节点的层级（性质5），加入任何黑色节点，都需要调整树

自平衡的原子操作

红黑树的自平衡包括：变色，旋转。其中旋转又可以分为左旋和右旋。旋转要 有圆心，有方向。
旋转节点围绕子节点旋转 （子节点为圆心）

| 旋转操作 | image.png | - 以圆心的上方判断是左旋还是右旋

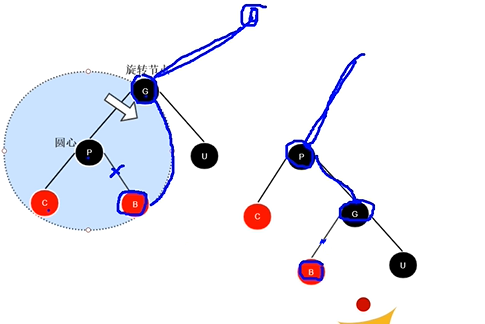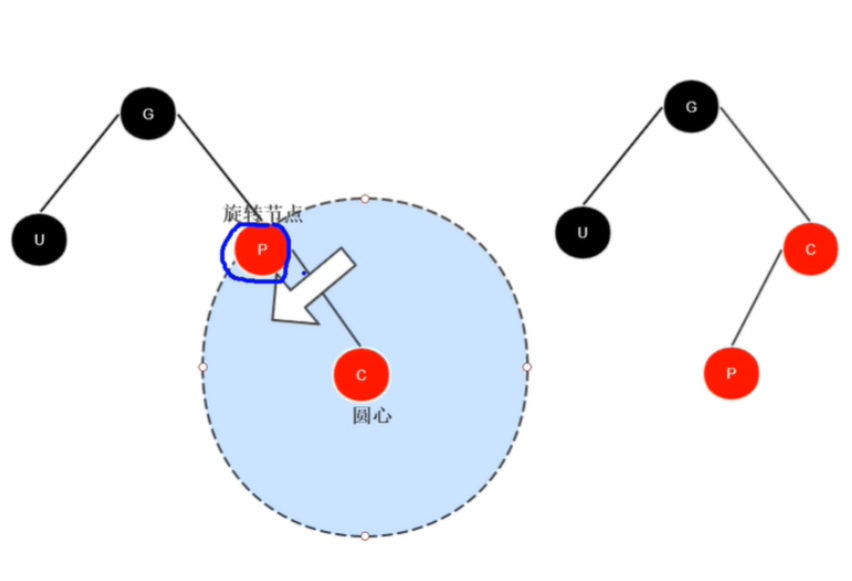  • 基于最短路劲判断是左旋还是右旋 | | :—-: | —- | —- | | 右旋操作 | image.png | 只要有节点旋转，就会产生互换 | | 左旋操作 | image.png | 旋转操作的圆心一定是它的子节点 |

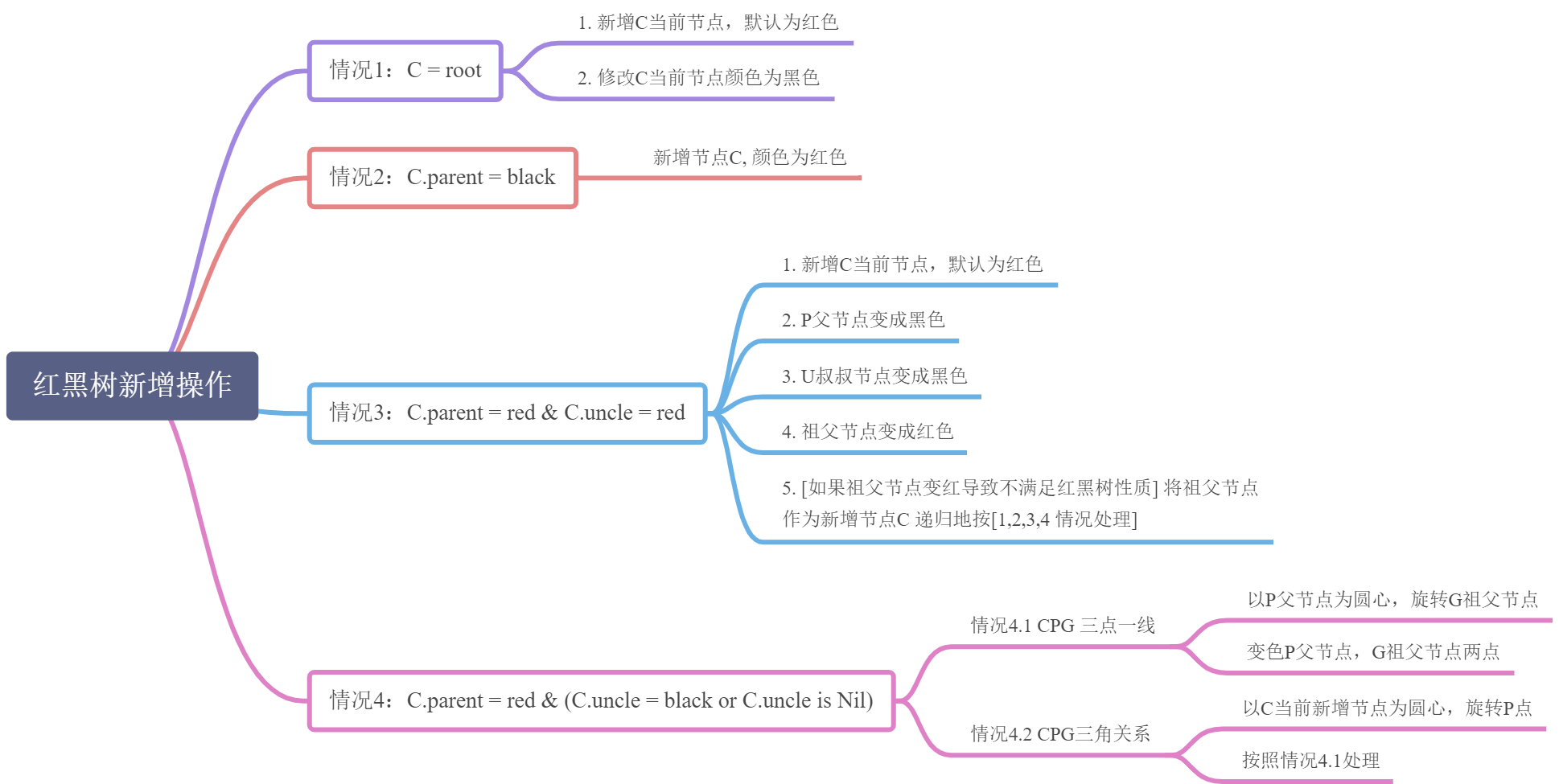
红黑树的新增操作

  • 情况1：C = root
  • 情况2：C.parent = black
  • 情况3：C.parent = red & C.uncle = red
  • 情况4：C.parent = red & (C.uncle = black or C.uncle is Nil) 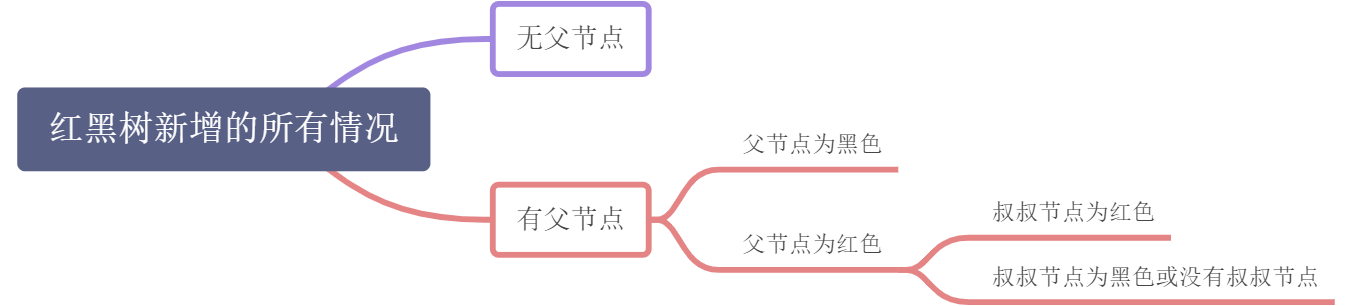红黑树 - 图12对于不同情况的具体操作： 红黑树 - 图13