一、简介

  • 数据结构：计算机存储、组织数据的方式，就像锅碗瓢盆
  • 算法：一系列解决问题的清晰指令，就像食谱
  • 程序 = 数据结构 + 算法


数据结构**

  • 栈、队列、链表
  • 集合、字典
  • 树、堆、图

算法

  • 链表：遍历链表、删除链表节点
  • 树、图：深度/广度优先遍历
  • 数组：冒泡/选择/插入/归并/快速排序、顺序/二分搜索

算法设计思想

  • 分而治之
  • 动态规划
  • 贪心算法
  • 回溯算法

算法解题四步分析法

  1. 模拟：模拟题目的运行
  2. 规律：尝试总结出题目的一般规律和特点
  3. 匹配：找到符合这些特点的数据结构与算法
  4. 边界：考虑特殊情况

二、时间复杂度与空间复杂度

1、时间复杂度

  • 一个函数，用大O表示，比如O(1)、O(n)、O(logN)
  • 定性描述该算法的运行时间（执行次数）

2、空间复杂度

  • 一个函数，用大O表示，比如O(1)、O(n)、O(n ^ 2)
  • 算法在运行过程中临时占用存储空间大小的量度（占用的内存单元）

三、栈

一个后进先出的数据结构

1、使用场景例子

  • 十进制转二进制
  • 有效的括号（LeetCode-20）
  • js函数调用堆栈

2、常用操作方式

  • push、pop、stack[stack.length - 1]

四、队列

一个先进先出的数据结构

1、使用场景例子

  • 食堂排队打饭
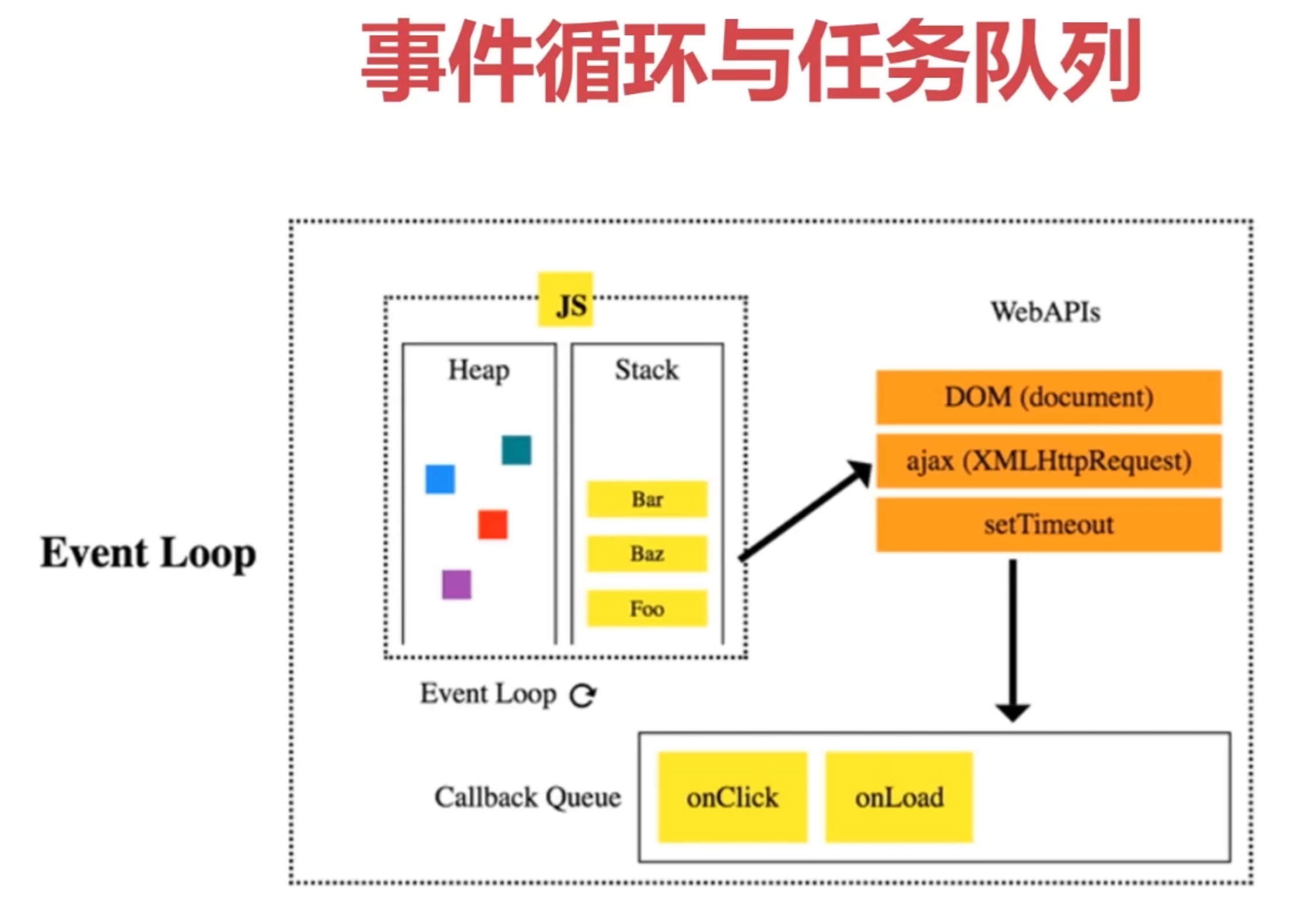
  • JS异步中的任务队列
  • 计算最近请求次数（LeetCode-933）

事件循环与任务队列.png

2、常用操作方式

  • push、shift、queue[0]

五、链表

  • 多个元素组成的列表
  • 元素存储不连续，用 next 指针连在一起
  • 在 js 中使用 Object 实现链表

1、链表和数组的区别

  • 数组：增删非首尾元素时往往需要移动元素
  • 链表：增删非首尾元素，不需要移动元素，只需要更改 next 的指向即可

2、链表创建方法及操作

  1. const a = { val: 'a' };
  2. const b = { val: 'b' };
  3. const c = { val: 'c' };
  4. const d = { val: 'd' };
  5. a.next = b;
  6. b.next = c;
  7. c.next = d;
  9. // 遍历链表
  10. let p = a;
  11. while (p) {
  12.     console.log(p.val);
  13.     p = p.next;
  14. }
  16. // 插入
  17. const e = { val: 'e' };
  18. c.next = e;
  19. e.next = d;
  21. // 删除
  22. c.next = d;

3、算法场景

  • 删除链表中的节点（LeetCode-237）
  • 反转链表（LeetCode-206）
  • 两数相加（LeetCode-2）
  • 删除排序链表中的重复元素（LeetCode-83）
  • 环形链表（LeetCode-141）

4、JS 中的链表 — 原型链

  • 原型链的本质是链表
  • 原型链上的节点是各种原型对象，比如 Function.prototype、Object.prototype
  • 原型链通过 __proto__ 属性链接各种原型对象

4.1 常见原型链

  • obj -> Object.prototype -> null
  • func -> Function.prototype -> Object.prototype -> null
  • arr -> Array.prototype -> Object.prototype -> null

4.2 原型链知识点

  • 如果 A 沿着原型链能找到 B.prototype，那么 A instanceof B 为 true
  1. // 手动实现 instanceof
  2. const instanceof = (A, B) => {
  3.     let p = A
  4.     while (p) {
  5.         if (p === B.prototype) {
  6.             return true
  7.         }
  8.         p = p.__proto__
  9.     }
  10.     return false
  11. }
  • 如果在 A 对象上没有找到 x 属性，那么会沿着原型链找 x 属性（如 toString）

5、JS 中的链表 — 使用链表指针获取 JSON 的节点值

  1. const json = {
  2.     a: { b: { c: 1 } },
  3.     d: { e: 2 },
  4. }
  6. const path = ['a', 'b', 'c']
  8. let p = json
  9. path.forEach(k => {
  10.     p = p[k]
  11. })

六、集合

  • 一种无序且唯一的数据结构
  • ES6 中有集合，名为 Set
  • 集合的常用操作：去重、判断某元素是否在集合中、求交集
  1. // 去重
  2. const arr = [1, 1, 2, 2]
  3. const arr2 = [...new Set(arr)]
  5. // 判断元素是否在集合中
  6. const set = new Set(arr)
  7. const has = set.has(1)
  9. // 求交集
  10. const set2 = new Set([2, 3])
  11. const set3 = new Set([...set].filter(v => set2.has(v)))

1、算法场景

  • 两个数组的交集（LeetCode-349）

2、ES6 的 Set

  • 使用 Set 对象：new、add、delete、has、size
  1. let mySet = new Set();
  3. mySet.add(1);
  4. mySet.add(5);
  5. mySet.add(5);
  6. mySet.add('some text');
  7. let o = { a: 1, b: 2 };
  8. mySet.add(o);
  9. mySet.add({ a: 1, b: 2 });
  11. const has = mySet.has(o);
  13. mySet.delete(5);
  14. console.log(mySet.size)
  • 迭代 Set：多种迭代方法、Set 与 Array 互转、求交集/差集
  1. // 三种迭代方法，其中第一、第二种等价
  2. for(let item of mySet.keys()) console.log(item)
  3. for(let item of mySet.values()) console.log(item)
  4. for(let [key, value] of mySet.entries()) console.log(key, value);
  5. mySet.forEach((value, key, current) => {})
  7. // Set 与 Array 互转
  8. const myArr = Array.from(mySet);
  9. const myArr2 = [...mySet]
  11. const mySet2 = new Set([1,2,3,4]);
  13. // 求交集/差集
  14. const intersection = new Set([...mySet].filter(x => mySet2.has(x)));
  15. const difference = new Set([...mySet].filter(x => !mySet2.has(x)));

七、字典

  • 与集合类似，也是存储唯一值的数据结构，但它是以键值对的形式来存储
  • ES6 中有字典，名为 Map
  • 常用操作：键值对的增删改查
  1. const m = new Map();
  3. // 增
  4. m.set('a', 'aa');
  5. m.set('b', 'bb');
  7. // 删
  8. m.delete('b');
  9. // m.clear();
  11. // 改
  12. m.set('a', 'aaa');
  14. // 查
  15. m.get('a')
  17. // 遍历和与数组互转，方法同集合(set)

1、算法场景

  • 两个数组的交集（LeetCode-349）
  • 有效的括号（LeetCode-20）
  • 两数之和（LeetCode-1）
  • 无重复字符的最长子串（LeetCode-3）
  • 最小覆盖子串（LeetCode-76）

八、树

  • 一种分层数据的抽象模型
  • 前端工作中常见的树包括：DOM树、级联选择、树形控件
  • JS中没有树，但是可以用 Object 和 Array 构建树
  • 常用操作：深度/广度优先遍历、先中后序遍历

1、深度/广度优先遍历

  • 深度优先遍历：尽可能深的搜索树的分支
  • 广度优先遍历：先访问离根节点最近的节点

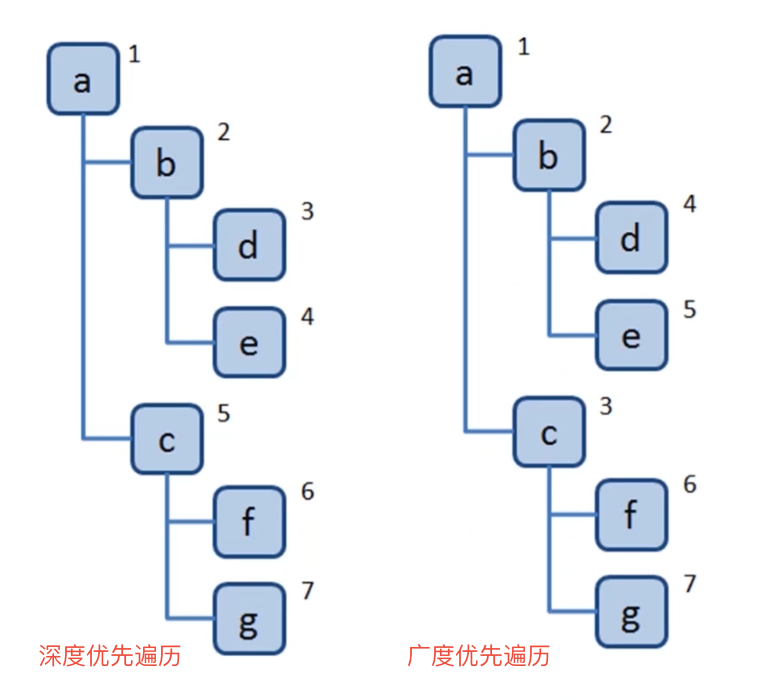
深度、广度优先遍历.png

1.1 深度优先遍历口诀

  1. 访问根节点
  2. 对根节点的 children 挨个进行深度优先遍历
  1. // dfs
  2. const tree = {
  3.     val: 'a',
  4.     children: [
  5.         {
  6.             val: 'b',
  7.             children: [
  8.                 {
  9.                     val: 'd',
  10.                     children: [],
  11.                 },
  12.                 {
  13.                     val: 'e',
  14.                     children: [],
  15.                 }
  16.             ],
  17.         },
  18.         {
  19.             val: 'c',
  20.             children: [
  21.                 {
  22.                     val: 'f',
  23.                     children: [],
  24.                 },
  25.                 {
  26.                     val: 'g',
  27.                     children: [],
  28.                 }
  29.             ],
  30.         }
  31.     ],
  32. };
  34. const dfs = (root) => {
  35.     console.log(root.val);
  36.     root.children.forEach(dfs);
  37. };
  39. dfs(tree);

1.2 广度优先遍历口诀

  1. 新建一个队列，把根节点入队
  2. 把队头出队并访问
  3. 把队头的 children 挨个入队
  4. 重复第二、三步，直到队列为空
  1. // bfs
  2. const tree = {
  3.     val: 'a',
  4.     children: [
  5.         {
  6.             val: 'b',
  7.             children: [
  8.                 {
  9.                     val: 'd',
  10.                     children: [],
  11.                 },
  12.                 {
  13.                     val: 'e',
  14.                     children: [],
  15.                 }
  16.             ],
  17.         },
  18.         {
  19.             val: 'c',
  20.             children: [
  21.                 {
  22.                     val: 'f',
  23.                     children: [],
  24.                 },
  25.                 {
  26.                     val: 'g',
  27.                     children: [],
  28.                 }
  29.             ],
  30.         }
  31.     ],
  32. };
  34. const bfs = (root) => {
  35.     const q = [root];
  36.     while (q.length > 0) {
  37.         const n = q.shift();
  38.         console.log(n.val);
  39.         n.children.forEach(child => {
  40.             q.push(child);
  41.         });
  42.     }
  43. };
  45. bfs(tree);

2、二叉树先中后序遍历

  • 树中每个节点最多只能有两个子节点
  • 在 JS 中通常用 Object 来模拟二叉树
  1. const binaryTree = {
  2.     val: 1,
  3.     left: {
  4.         val: 2,
  5.         left: null,
  6.         right: null
  7.     },
  8.     right: {
  9.         val: 3,
  10.         left: null,
  11.         right: null
  12.     }
  13. }

2.1 先序遍历算法口诀

  1. 访问根节点
  2. 对根节点的左子树进行先序遍历
  3. 对根节点的右子树进行先序遍历

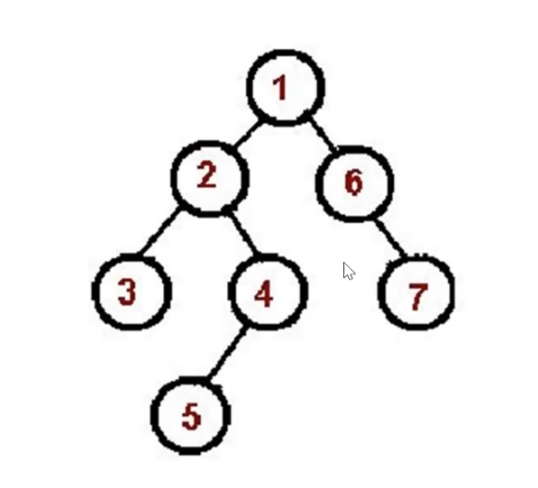
先序遍历.png

  1. // preorder
  2. const bt = {
  3.     val: 1,
  4.     left: {
  5.         val: 2,
  6.         left: {
  7.             val: 4,
  8.             left: null,
  9.             right: null,
  10.         },
  11.         right: {
  12.             val: 5,
  13.             left: null,
  14.             right: null,
  15.         },
  16.     },
  17.     right: {
  18.         val: 3,
  19.         left: {
  20.             val: 6,
  21.             left: null,
  22.             right: null,
  23.         },
  24.         right: {
  25.             val: 7,
  26.             left: null,
  27.             right: null,
  28.         },
  29.     },
  30. };
  32. // 递归版
  33. const preorder = (root) => {
  34.     if (!root) { return; }
  35.     console.log(root.val);
  36.     preorder(root.left);
  37.     preorder(root.right);
  38. };
  40. // 非递归版
  41. const preorder = (root) => {
  42.     if (!root) { return; }
  43.     const stack = [root]
  44.     while (stack.length) {
  45.         const n = stack.pop()
  46.         console.log(n.val)
  47.         if (n.right) stack.push(n.right)
  48.         if (n.left) stack.push(n.left)
  49.     }
  50. };
  52. preorder(bt);

2.2 中序遍历算法口诀

  1. 对根节点的左子树进行中序遍历
  2. 访问根节点
  3. 对根节点的右子树进行中序遍历

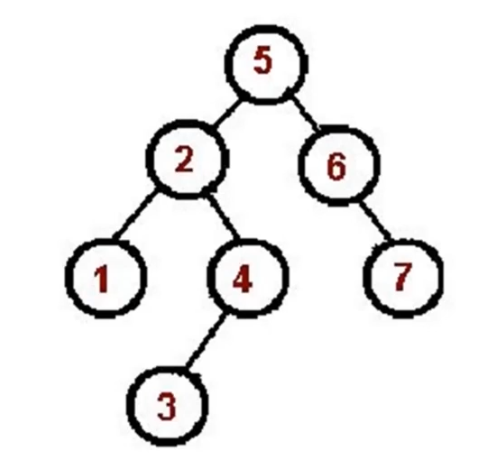
中序遍历.png

  1. // inorder
  2. // 递归版
  3. const inorder = (root) => {
  4.     if (!root) { return; }
  5.     inorder(root.left);
  6.     console.log(root.val);
  7.     inorder(root.right);
  8. };
  10. // 非递归版
  11. const inorder = (root) => {
  12.     if (!root) { return; }
  13.     const stack = []
  14.     let p = root
  15.     while (stack.length || p) {
  16.         while (p) {
  17.             stack.push(p)
  18.             p = p.left 
  19.         }
  20.         const n = stack.pop()
  21.         console.log(n.val)
  22.         p = n.right
  23.     }
  24. };
  26. inorder(bt);

2.3 后序遍历算法口诀

  1. 对根节点的左子树进行中序遍历
  2. 对根节点的右子树进行中序遍历
  3. 访问根节点

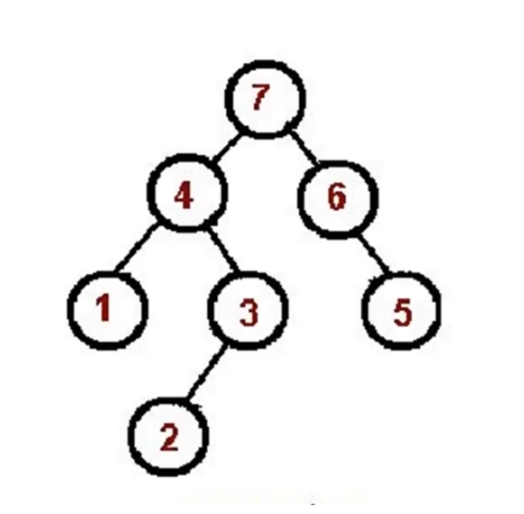
后序遍历.png

  1. // postorder
  2. // 递归版
  3. const inorder = (root) => {
  4.     if (!root) { return; }
  5.     inorder(root.left);
  6.     inorder(root.right);
  7.     console.log(root.val);
  8. };
  10. // 非递归版
  11. // 逆序思考，类似先序遍历（根右左）
  12. const postorder = (root) => {
  13.     if (!root) { return; }
  14.     const stack = [root]
  15.     const outputStack = []
  16.     while (stack.length) {
  17.         const n = stack.pop()
  18.         outputStack.push(n)
  19.         if (n.left) stack.push(n.left)
  20.         if (n.right) stack.push(n.right)
  21.     }
  22.     while (outputStack.length) {
  23.         const n = outputStack.pop()
  24.         console.log(n.val)
  25.     }
  26. };
  28. postorder(bt);

3、算法场景

  • 二叉树的最大深度（LeetCode-104）
  • 二叉树的最小深度（LeetCode-111）
  • 二叉树的层序遍历（LeetCode-102）
  • 二叉树的中序遍历（LeetCode-94）
  • 路径总和（LeetCode-112）

4、前端与树

  • 遍历 JSON 的所有节点值
  1. const json = {
  2.     a: { b: { c: 1 } },
  3.     d: [1, 2],
  4. };
  6. const dfs = (n, path) => {
  7.     console.log(n, path);
  8.     Object.keys(n).forEach(k => {
  9.         dfs(n[k], path.concat(k));
  10.     });
  11. };
  13. dfs(json, []);
  • 渲染 Antd 的树组件

九、图

  • 图是网络结构的抽象，是一组由边连接的节点
  • 图可以表示任何二元关系，比如道路、航班等
  • JS 中没有图，但是可以用 Object 和 Array 构建图
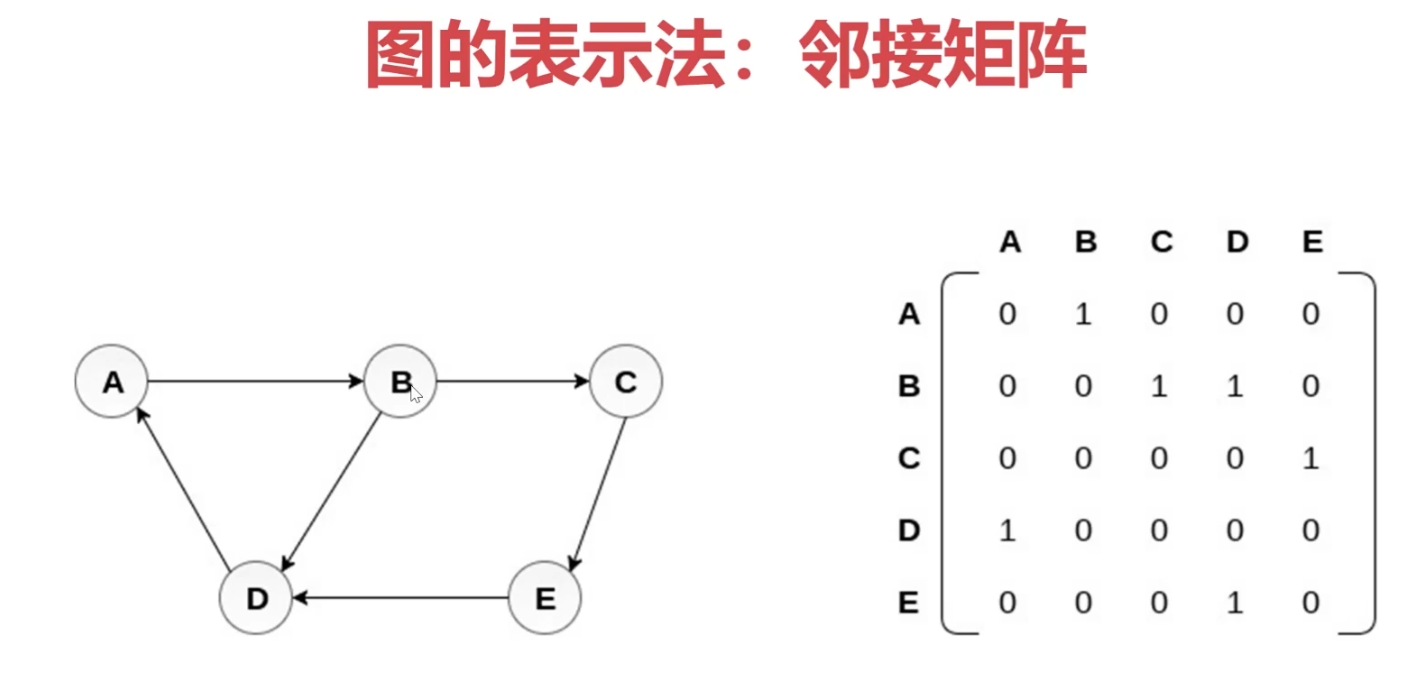
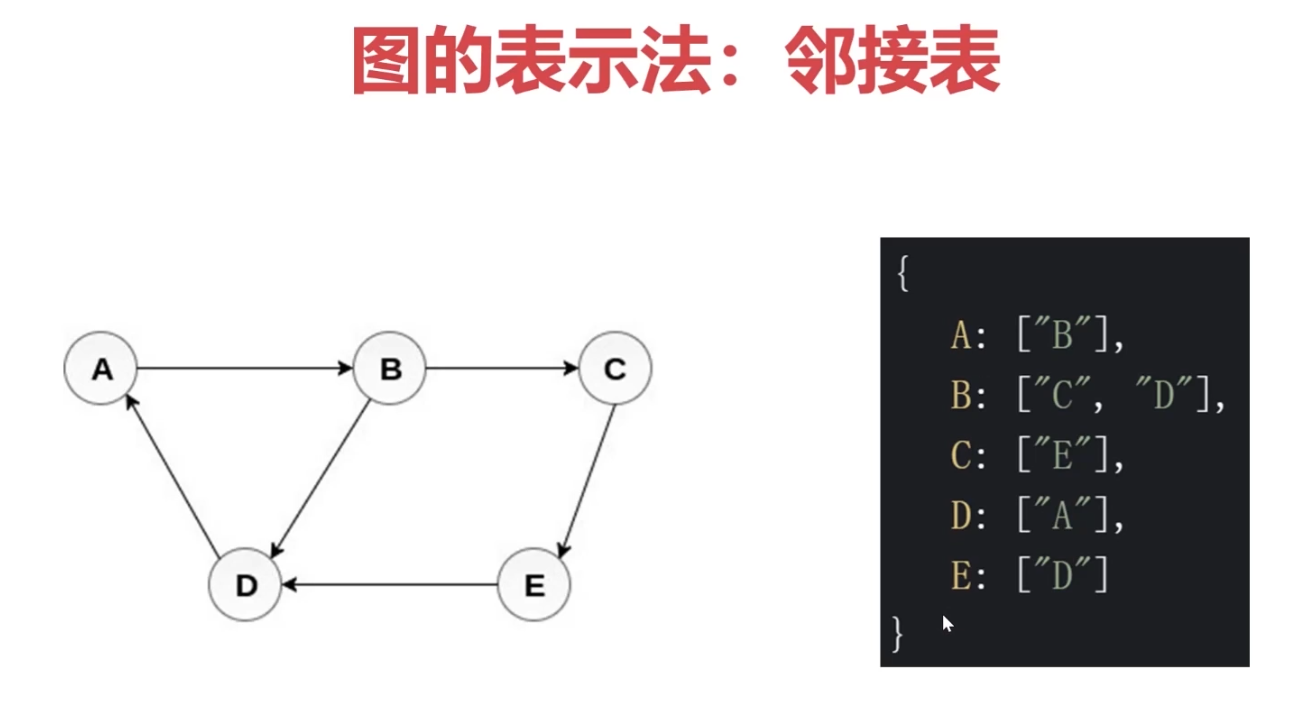
  • 图的表示法：邻接矩阵、邻接表、关联矩阵等
  • 常用操作：深度/广度优先遍历

邻接矩阵.png
邻接表.png

1、图的深度/广度优先遍历

  • 深度优先遍历：尽可能深的搜索图的分支
  • 广度优先遍历：先访问离根节点最近的节点

1.1 深度优先遍历口诀

  1. 访问根节点
  2. 对根节点的没访问过的相邻节点挨个进行深度优先遍历

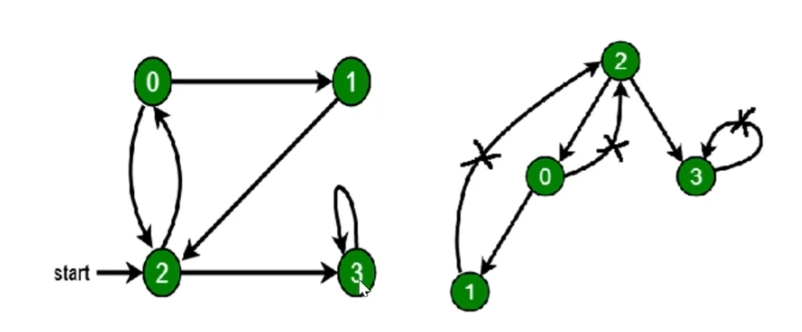
图-深度优先遍历.png

  1. const graph = {
  2.   0: [1, 2],
  3.   1: [2],
  4.   2: [0, 3],
  5.   3: [3]
  6. };
  8. const visited = new Set()
  9. const dfs = (n) => {
  10.   console.log(n)
  11.   visited.add(n)
  12.   graph[n].forEach(c => {
  13.       if (!visited.has(c)) {
  14.         dfs(c)
  15.     }
  16.   })
  17. }

1.2 广度优先遍历口诀

  1. 新增一个队列，把根节点入队
  2. 把队头出队并访问
  3. 把队头的没访问过的相邻节点入队
  4. 重复第二、三步直到队列为空

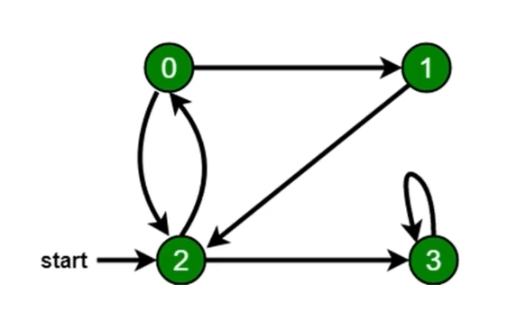
图-广度优先遍历.png

  1. const graph = {
  2.   0: [1, 2],
  3.   1: [2],
  4.   2: [0, 3],
  5.   3: [3]
  6. };
  8. const bfs = (root) => {
  9.   const visited = new Set()
  10.   visited.add(root)
  11.     const q = [root]
  12.   while(q.length) {
  13.       const n = q.shift()
  14.       console.log(n)
  15.       graph[n].forEach(c => {
  16.           if (!visited.has(c)) {
  17.             q.push(c)
  18.         visited.add(c)
  19.         } 
  20.     })
  21.   }
  22. }

2、算法场景

  • 有效数字（LeetCode-65）
  • 太平洋大西洋水流问题（LeetCode-417）
  • 克隆图（LeetCode-133）

十、堆

堆.png

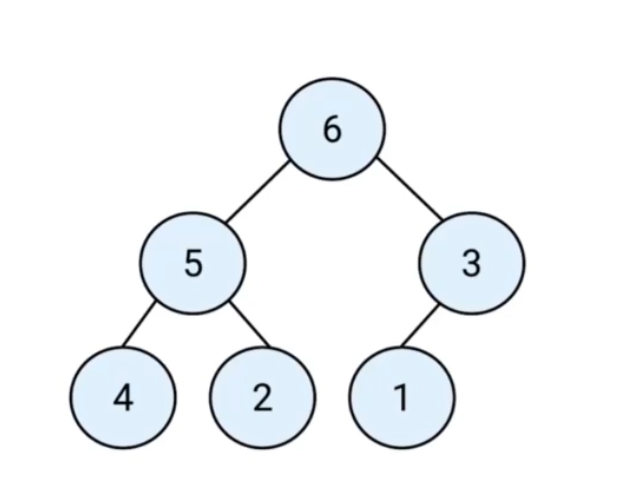
  • 堆是一种特殊的完全二叉树（节点完全填满，只能剩余右侧的节点）
  • 所有的节点都大于等于（最大堆）或小于等于（最小堆）它的子节点

1、JS 中的堆

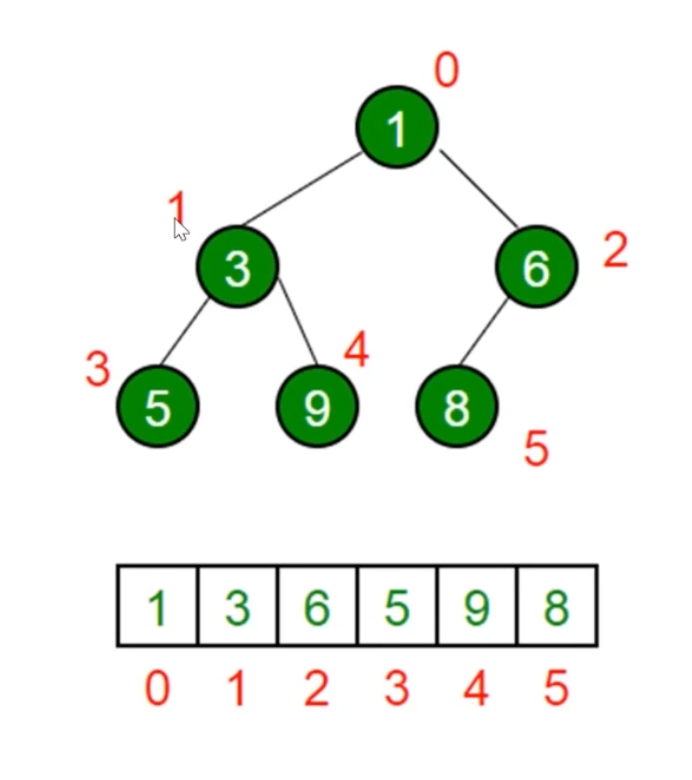
js中的堆.png

  • JS 中通常用数组来表示堆
  • 左侧子节点的位置是2 * index + 1
  • 右侧子节点的位置是2 * index + 2
  • 父节点的位置是 (index - 1) / 2

2、堆的应用

  • 堆能高效、快速地找出最大/最小值，时间复杂度是 O(1)
  • 找出第 k 个最大（小）元素

2.1 找出第 k 个最大（小）元素

第K个最大元素.png

2.2 最小堆类实现

  • 在类中，声明一个数组，用来装元素
  • 主要方法：插入、删除堆顶、获取堆顶、获取堆大小

插入
  1. 将值插入堆的底部，即数组的尾部
  2. 然后上移：将这个值和它的父节点进行交换，直到父节点小于等于这个插入的值

大小为 k 的堆中插入元素的时间复杂度为 O(logk)

删除堆顶
  1. 用数组尾部元素替换堆顶（直接删除堆顶会破坏堆结构）
  2. 然后下移：将新堆顶和它的子节点进行交换，直到子节点大于等于这个新堆顶

大小为 k 的堆中删除堆顶的时间复杂度为 O(logk)

获取堆顶和堆的大小
  • 获取堆顶：返回数组的头部

  • 获取堆的大小：返回数组的长度 ```javascript class MinHeap { constructor() { this.heap = [] }

    swap(i1, i2) { const temp = this.heap[i1] this.heap[i1] = this.heap[i2] this.heap[i2] = temp }

    getParentIndex(i) { return (i - 1) >> 1 // return Math.floor((i - 1) / 2) }

    getLeftIndex(i) { return i * 2 + 1 }

    getRightIndex(i) { return i * 2 + 2 }

    shiftUp(index) { if (index === 0) return const parentIndex = this.getParentIndex(index) if (this.heap[parentIndex] > this.heap[index]) {

    1. this.swap(parentIndex, index)
    2. this.shiftUp(parentIndex)

    } }

    shiftDown(index) { const leftIndex = this.getLeftIndex(index) const rightIndex = this.getRightIndex(index)

    if (this.heap[leftIndex] < this.heap[index]) {

    1. this.swap(leftIndex, index)
    2. this.shiftDown(leftIndex)

    } if (this.heap[rightIndex] < this.heap[index]) {

    1. this.swap(rightIndex, index)
    2. this.shiftDown(rightIndex)

    } }

    // 插入方法 insert(value) { this.heap.push(value) this.shiftUp(this.heap.length - 1) }

    // 删除方法 pop() { this.heap[0] = this.heap.pop() this.shiftDown(0) }

    // 获取堆顶 top() { return this.heap[0] }

    // 获取堆大小 size() { return this.heap.length } }

// 示例 const h = new MinHeap() h.insert(3) h.insert(2) h.insert(1) h.pop()

  1. <a name="GlNGh"></a>
  2. ### 3、算法场景
  4. - 数组中的第 K 个最大元素（LeetCode-215）
  5. - 前 K 个高频元素（LeetCode-347）
  6. - 合并 K 个排序链表（LeetCode-23）
  8. <a name="uVEvR"></a>
  9. ## 十一、搜索排序
  10. <a name="WWed6"></a>
  11. ### 1、排序
  12. 把某个乱序的数组变成升序或者降序的数组，JS 中的排序如 sort 方法，常见排序算法如下：
  13. <a name="swz6I"></a>
  14. #### 1.1 冒泡排序
  15. **思路：**
  17. 1. 比较所有相邻元素，如果第一个比第二个大，则交换它们
  18. 2. 一轮下来可以保证最后一个数是最大的
  19. 3. 执行 n - 1 轮，就可以完成排序 
  21. **<br />**代码实现：**
  22. ```javascript
  23. // 时间复杂度 O(n^2)
  24. // 升序
  25. Array.prototype.bubbleSort = function () {
  26.   for (let i = 0; i < this.length - 1; i += 1) {
  27.     for (let j = 0; j < this.length - 1 - i; j += 1) {
  28.       if (this[j] > this[j + 1]) {
  29.         const temp = this[j]
  30.         this[j] = this[j + 1]
  31.         this[j + 1] = temp
  32.       }
  33.     }
  34.   }
  35. }
  37. const arr = [5, 4, 3, 2, 1]
  38. arr.bubbleSort()
  39. console.log(arr)

1.2 选择排序

思路：

  1. 找到数组中的最小值，选中它并将其放置在第一位
  2. 接着找到第二小的值，选中它并将其放置在第二位
  3. 以此类推，执行 n - 1 轮


代码实现：**

  1. // 时间复杂度 O(n^2)
  2. // 升序
  3. Array.prototype.selectionSort = function () {
  4.   for (let i = 0; i < this.length - 1; i += 1) {
  5.     let minIndex = i
  6.     for (let j = i + 1; j < this.length; j += 1) {
  7.       if (this[minIndex] > this[j]) {
  8.         minIndex = j
  9.       }
  10.     }
  11.     if (i !== minIndex) {
  12.       const temp = this[i]
  13.       this[i] = this[minIndex]
  14.       this[minIndex] = temp
  15.     }
  16.   }
  17. }
  19. const arr = [5, 4, 3, 2, 1]
  20. arr.selectionSort()
  21. console.log(arr)

1.3 插入排序

思路：

  1. 从第二个数开始，将其“提取”往前比
  2. 比它大就往后移一格，否则将其插入
  3. 以此类推进行到最后一个数


代码实现：**

  1. // 时间复杂度 O(n^2)
  2. // 升序
  3. Array.prototype.insertSort = function () {
  4.   for (let i = 1; i < this.length; i += 1) {
  5.     const temp = this[i]
  6.     for (let j = i - 1; j >= 0; j -= 1) {
  7.       if (this[j] > temp) {
  8.         this[j + 1] = this[j]
  9.         this[j] = temp
  10.       } else {
  11.         break
  12.       }
  13.     }
  14.   }
  15. }
  17. const arr = [5, 4, 3, 2, 1]
  18. arr.insertSort()
  19. console.log(arr)

1.4 归并排序

思路：

  1. 分：把数组劈成两半，再递归地对子数组进行“分”操作，直到分成一个个单独的数
  2. 合：把两个数合并为有序数组，再对有序数组进行合并，直到全部子数组合并为一个完整数组

合并两个有序数组：

  1. 新建一个空数组 res，用于存放最终排序后的数组
  2. 比较两个有序数组的头部，较小者出队并推入 res 中
  3. 如果两个数组还有值，就重复第二步


代码实现：**

  1. // 时间复杂度 O(nlogn)
  2. // 升序
  3. Array.prototype.mergeSort = function () {
  4.   const rec = (arr) => {
  5.     if (arr.length === 1) return arr
  6.     const mid = Math.floor(arr.length / 2)
  7.     const left = arr.slice(0, mid)
  8.     const right = arr.slice(mid, arr.length)
  9.     const orderLeft = rec(left)
  10.     const orderRight = rec(right)
  11.     const res = []
  12.     while (orderLeft.length || orderRight.length) {
  13.       if (orderLeft.length && orderRight.length) {
  14.         res.push(orderLeft[0] < orderRight[0] ? orderLeft.shift() : orderRight.shift())
  15.       } else if (orderLeft.length) {
  16.         res.push(orderLeft.shift())
  17.       } else if (orderRight.length) {
  18.         res.push(orderRight.shift())
  19.       }
  20.     }
  21.     return res
  22.   }
  23.   const res = rec(this)
  24.   res.forEach((v, i) => {
  25.     this[i] = v
  26.   })
  27. }
  29. const arr = [5, 4, 3, 2, 1]
  30. arr.mergeSort()
  31. console.log(arr)

1.5 快速排序

思路：

  1. 分区：从数组中任意选择一个“基准”，所有比基准小的元素放在基准前面，比基准大的元素放在基准的后面
  2. 递归：递归地对基准前后的子数组进行分区


代码实现：**

  1. // 时间复杂度 O(nlogn)
  2. // 升序
  3. Array.prototype.quickSort = function () {
  4.   const rec = (arr) => {
  5.     if (arr.length <= 1) return arr
  6.     const left = []
  7.     const right = []
  8.     const mid = arr[0]
  9.     for (let i = 1; i < arr.length; i += 1) {
  10.       if (arr[i] < mid) {
  11.         left.push(arr[i])
  12.       } else {
  13.         right.push(arr[i])
  14.       }
  15.     }   
  16.     return [...rec(left), mid, ...rec(right)]
  17.   }
  18.   const res = rec(this)
  19.   res.forEach((v, i) => {
  20.     this[i] = v
  21.   })
  22. }
  24. const arr = [5, 4, 3, 2, 1]
  25. arr.quickSort()
  26. console.log(arr)

2、搜索

找出数组中某个元素的下标，JS 中的搜索如 indexOf、findIndex等方法，常见搜索算法如下：

2.1 顺序搜索

思路：

  1. 遍历数组
  2. 找到跟目标值相等的元素，就返回它的下标
  3. 遍历结束后，如果没找到，就返回 -1


代码实现：**

  1. // 时间复杂度 O(n)
  2. Array.prototype.sequentialSearch = function (target) {
  3.   for(let i = 0; i < this.length; i += 1) {
  4.     if (this[i] === target) return i
  5.   }
  6.   return -1
  7. }
  9. const arr = [5, 4, 3, 2, 1]
  10. const index = arr.sequentialSearch(2)
  11. console.log(index)

2.2 二分搜索

必须有序
思路：

  1. 从数组的中间元素开始，如果中间元素正好是目标值，则搜索结束
  2. 如果目标值大于或小于中间元素，则在大于或小于中间元素的那一半数组中搜索


代码实现：**

  1. // 时间复杂度 O(logn)
  2. Array.prototype.binarySearch = function (target) {
  3.   let begin = 0
  4.   let end = this.length - 1
  5.   while (begin <= end) {
  6.     const mid = Math.floor((end + begin) / 2)
  7.     if (this[mid] === target) {
  8.       return mid
  9.     } else if (this[mid] < target) {
  10.       begin = mid + 1
  11.     } else if (this[mid] > target) {
  12.       end = mid - 1
  13.     }
  14.   }
  15.   return -1
  16. }
  18. const arr = [1, 2, 3, 4, 5]
  19. const index = arr.binarySearch(2)
  20. console.log(index)

3、算法场景

  • 合并两个有序链表（LeetCode-21）
  • 猜数字大小（LeetCode-374）

十二、分而治之

  • 分而治之是算法设计中的一种方法，是一种思想
  • 它将一个问题分成多个和原问题相似的小问题，递归解决小问题，再将结果合并以解决原来的问题

1、场景一：归并排序

  • 分：把数组从中间一分为二
  • 解：递归地对两个子数组进行归并排序
  • 合：合并有序子数组

2、场景二：快速排序

  • 分：选基准，按基准把数组分成两个子数组
  • 解：递归地对两个子数组进行快速排序
  • 合：对两个子数组进行合并

3、算法场景

  • 猜数字大小（LeetCode-374）
  • 翻转二叉树（LeetCode-226）
  • 相同的树（LeetCode-100）
  • 对称二叉树（LeetCode-101）

十三、动态规划

  • 动态规划是算法设计中的一种方法，是一种思想
  • 它将一个问题分解为相互重叠的子问题，通过反复求解子问题，来解决原来的问题

何为相互重叠呢？看一个典型的例子，斐波那契数列
斐波那契数列.png

1、动态规划 vs 分而治之

  • 相同点：动态规划和分而治之都是将一个问题分解为子问题
  • 不同点：动态规划是相互重叠的子问题，子问题之间有关联关系；分而治之的子问题彼此相互独立

2、算法场景

  • 爬楼梯（LeetCode-70）
  • 打家劫舍（LeetCode-198）

十四、贪心算法

  • 贪心算法是算法设计中的一种方法，是一种思想
  • 期盼通过每个阶段的局部最优选择，从而达到全局的最优
  • 结果并不一定是最优

1、算法场景

  • 分饼干（LeetCode-455）
  • 买卖股票的最佳时机（LeetCode-122）

十五、回溯算法

  • 回溯算法是算法设计中的一种方法，是一种思想
  • 回溯算法是一种渐进式寻找并构建问题解决方式的策略
  • 回溯算法会先从一个可能的动作开始解决问题，如果不行，就回溯并选择另一个动作，直到将问题解决


1、适用场景

  • 有很多路
  • 这些路里，有死路，也有出路
  • 通常需要递归来模拟所有的路

以全排列为例：
全排列.png

2、算法场景

  • 全排列（LeetCode-46）
  • 子集（LeetCode-78）