数据结构概念：数据结构是计算机存储、组织数据的方式。数据结构是指相互之间存在一种或多种特定关系的数据元素的集合。通常情况下，精心选择的数据结构可以带来更高的运行或者存储效率。数据结构往往同高效的检索算法和索引技术有关。
常用数据结构：数组(Array)、栈(Stack)、队列(Queue)、链表(Linked List)、树(Tree)、图(Graph)、堆(Heap)、散列表(Hash)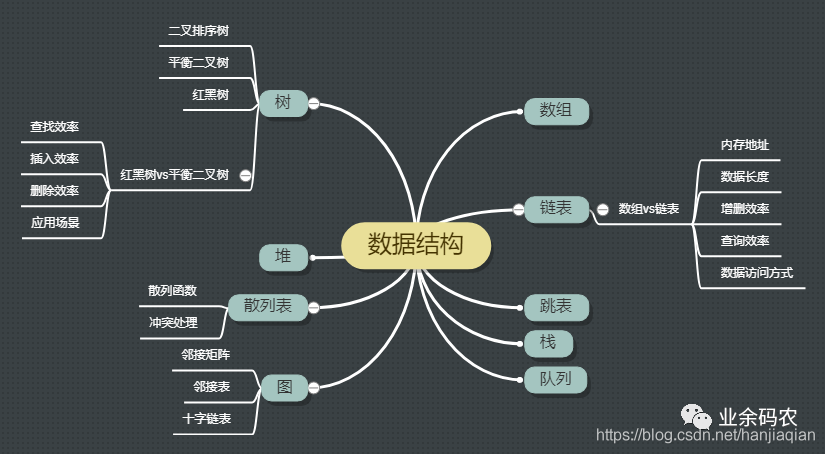
image.png
算法的意义： 算法研究的目的是为了更有效的处理数据，提高数据运算效率。数据的运算是定义在数据的逻辑结构上，但运算的具体实现要在存储结构上进行。

一、树的遍历

树的遍历分为两类：

  • 深度优先（DFS）
    • 前序遍历
    • 中序遍历
    • 后序遍历
  • 广度优先（BFS）
    • 层次遍历

      准备：定义节点

      1. public class TreeNode {
      2. String value = null; // 根节点
      3. TreeNode leftChildren = null; // 左子节点
      4. TreeNode rightChildren = null; // 右子节点
      5. public TreeNode(String value, TreeNode leftChildren, TreeNode rightChildren) {
      6.    this.value = value;
      7.    this.leftChildren = leftChildren;
      8.    this.rightChildren = rightChildren;
      9. }
      10. public TreeNode(String value) {
      11.    this.value = value;
      12. }
      13. public void setValue(String value) {
      14.    this.value = value;
      15. }
      16. public void setLeftChildren(TreeNode leftChildren) {
      17.    this.leftChildren = leftChildren;
      18. }
      19. public void setRightChildren(TreeNode rightChildren) {
      20.    this.rightChildren = rightChildren;
      21. }
      22. public String getValue() {
      23.    return value;
      24. }
      25. public TreeNode getLeftChildren() {
      26.    return leftChildren;
      27. }
      28. public TreeNode getRightChildren() {
      29.    return rightChildren;
      30. }
      31. }

      1、深度优先(DFS)

      1.1、前序遍历
      思路：先根节点->左子树->右子树；
      结构如下：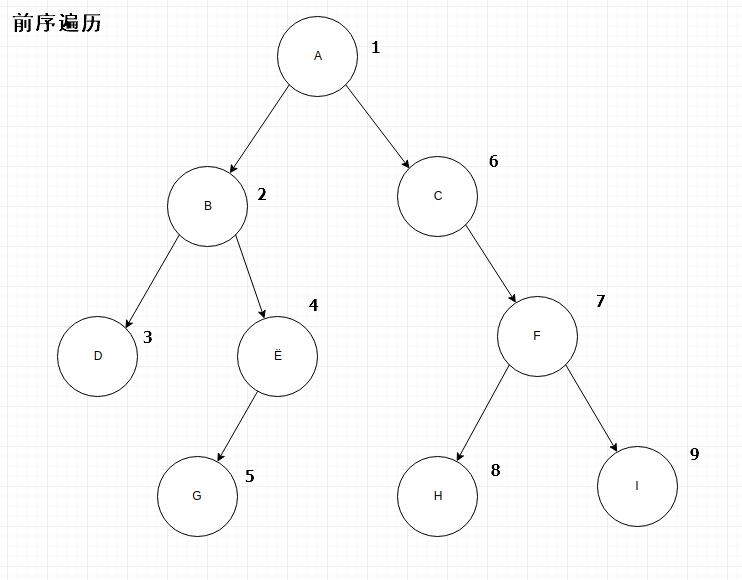
      image.png ```java

public class TreeSearch {

  1. public TreeNode getTargetTree() {
  2.     // 叶子节点
  3.     TreeNode G = new TreeNode("G");
  4.     TreeNode D = new TreeNode("D");
  5.     TreeNode E = new TreeNode("E", G, null);
  6.     TreeNode B = new TreeNode("B", D, E);
  7.     TreeNode H = new TreeNode("H");
  8.     TreeNode I = new TreeNode("I");
  9.     TreeNode F = new TreeNode("F", H, I);
  10.     TreeNode C = new TreeNode("C", null, F);
  11.     // 构造根节点
  12.     TreeNode root = new TreeNode("A", B, C);
  13.     return root;
  14. }
  16. /**
  17.  * 前序遍历 先根节点->左子树->右子树；
  18.  */
  19. public void preOrderVisitTreeNode(TreeNode node) {
  20.     if (null != node) {
  22.         System.out.print(node.value);
  24.         if (null != node.getLeftChildren()) {
  25.             preOrderVisitTreeNode(node.getLeftChildren());
  26.         }
  27.         if (null != node.getRightChildren()) {
  28.             preOrderVisitTreeNode(node.getRightChildren());
  29.         }
  30.     }
  31. }
  34. public static void main(String[] args) {
  36.     TreeTest treeSearch = new TreeTest();
  37.     TreeNode tree = treeSearch.getTargetTree();
  39.     System.out.print("前序遍历:");
  40.     treeSearch.preOrderVisitTreeNode(tree);
  41.     System.out.println("");    
  42. }

} //先序遍历:ABDEGCFHI

  1. **1.2、中序遍历**<br /> 思路：先左子树->根节点->右子树；<br />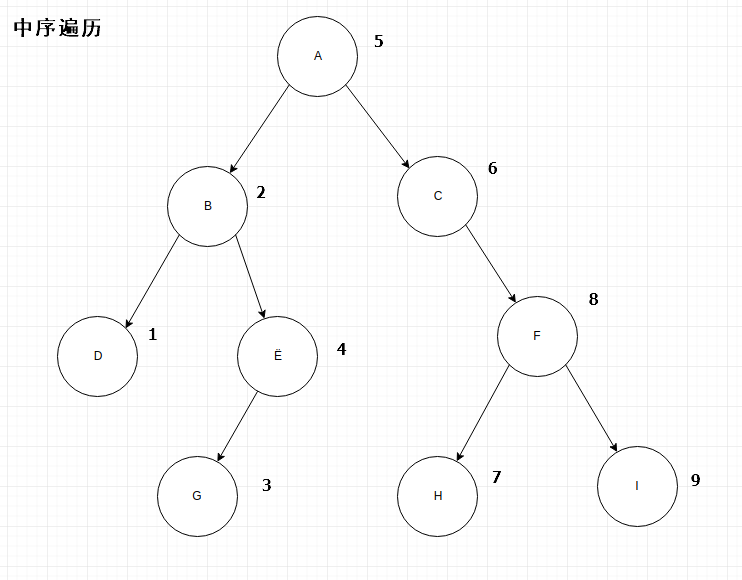![image.png](https://cdn.nlark.com/yuque/0/2022/png/26093269/1652165499146-dff77ea6-f6ad-42b5-bb98-b5a13b2a2dac.png#clientId=ube2d197e-b664-4&crop=0&crop=0&crop=1&crop=1&from=paste&id=u203ea0fb&margin=%5Bobject%20Object%5D&name=image.png&originHeight=580&originWidth=742&originalType=url&ratio=1&rotation=0&showTitle=false&size=51992&status=done&style=none&taskId=uaec5a546-1231-4a18-9a82-c0312c4737d&title=)
  2. ```java
  3. public class TreeSearch { 
  4.       public TreeNode getTargetTree() {
  5.         // 叶子节点
  6.         TreeNode G = new TreeNode("G");
  7.         TreeNode D = new TreeNode("D");
  8.         TreeNode E = new TreeNode("E", G, null);
  9.         TreeNode B = new TreeNode("B", D, E);
  10.         TreeNode H = new TreeNode("H");
  11.         TreeNode I = new TreeNode("I");
  12.         TreeNode F = new TreeNode("F", H, I);
  13.         TreeNode C = new TreeNode("C", null, F);
  14.         // 构造根节点
  15.         TreeNode root = new TreeNode("A", B, C);
  16.         return root;
  17.     }
  19.     /**
  20.      *  中序遍历 先左子树->根节点->右子树；
  21.      */
  22.     public void inorderVisitTreeNode(TreeNode node) {
  23.         if (null != node) {
  24.             if (null != node.getLeftChildren()) {
  25.                 inorderVisitTreeNode(node.getLeftChildren());
  26.             }
  28.             System.out.print(node.value);
  30.             if (null != node.getRightChildren()) {
  31.                 inorderVisitTreeNode(node.getRightChildren());
  32.             }
  33.         }
  34.     }
  36.     public static void main(String[] args) {
  37.         TreeTest treeSearch = new TreeTest();
  38.         TreeNode tree = treeSearch.getTargetTree();
  40.         System.out.print("中序遍历:");
  41.         treeSearch.inorderVisitTreeNode(tree);
  42.         System.out.println("");
  43.     }
  44. }
  45. //中序遍历:DBGEACHFI

1.3、后续遍历
思路：先左子树->右子树->根节点；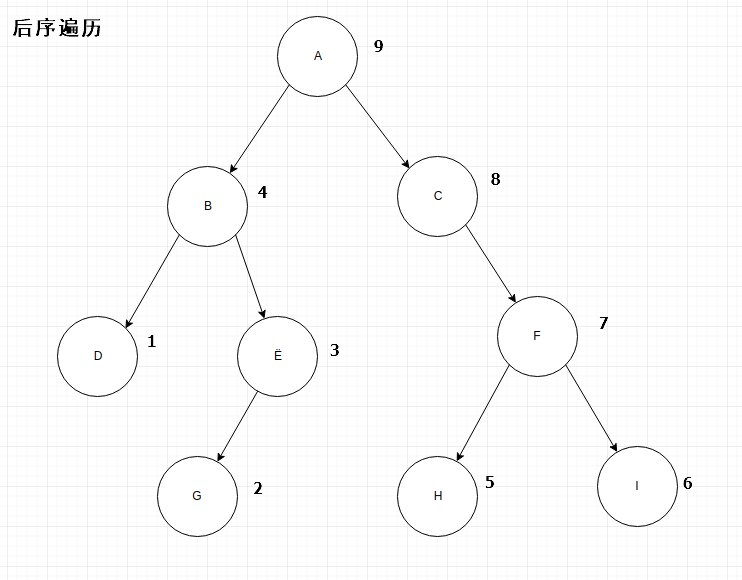
image.png

  1. public class TreeSearch { 
  2.       public TreeNode getTargetTree() {
  3.         // 叶子节点
  4.         TreeNode G = new TreeNode("G");
  5.         TreeNode D = new TreeNode("D");
  6.         TreeNode E = new TreeNode("E", G, null);
  7.         TreeNode B = new TreeNode("B", D, E);
  8.         TreeNode H = new TreeNode("H");
  9.         TreeNode I = new TreeNode("I");
  10.         TreeNode F = new TreeNode("F", H, I);
  11.         TreeNode C = new TreeNode("C", null, F);
  12.         // 构造根节点
  13.         TreeNode root = new TreeNode("A", B, C);
  14.         return root;
  15.     }
  16.     /**
  17.      *  后序遍历 先左子树->右子树->根节点；
  18.      */
  19.     public void postOrderVisitTreeNode(TreeNode node) {
  20.         if (null != node) {
  21.             if (null != node.getLeftChildren()) {
  22.                 postOrderVisitTreeNode(node.getLeftChildren());
  23.             }
  24.             if (null != node.getRightChildren()) {
  25.                 postOrderVisitTreeNode(node.getRightChildren());
  26.             }
  28.             System.out.print(node.value);
  29.         }
  30.     }
  32.     public static void main(String[] args) {
  33.        TreeTest treeSearch = new TreeTest();
  34.        TreeNode tree= treeSearch.getTargetTree();
  36.         System.out.print("后序遍历:");
  37.         treeSearch.postOrderVisitTreeNode(tree);
  38.         System.out.println("");
  39.     }
  40. //结果：后序遍历:DGEBHIFCA

2、广度优先

2.1、层次遍历
思路：先根节点，然后第二层，第三层，依次往下走，（同层节点从左往右输出）;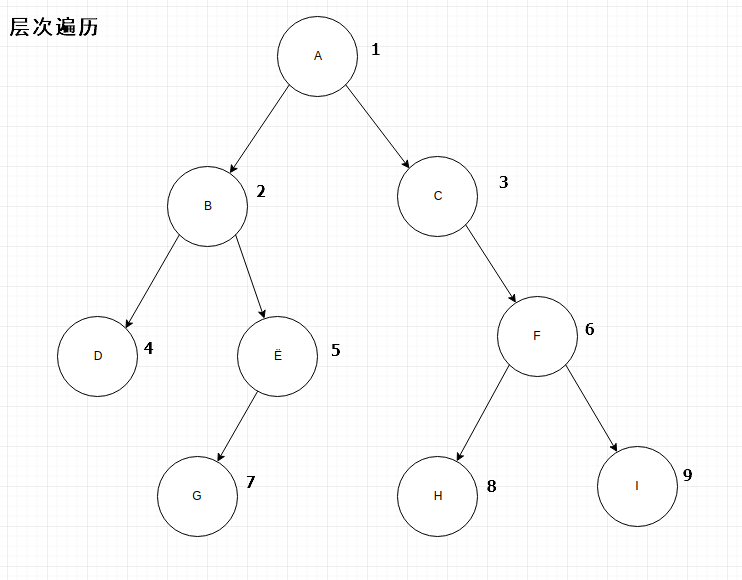
image.png
层序遍历:ABCDEFGHI
层序遍历二叉树，是非递归的队列实现的，就是利用队列的先进先出（FIFO）实现的。

  1. public class TreeTest {
  3.     public TreeNode getTargetTree() {
  4.         // 叶子节点
  5.         TreeNode G = new TreeNode("G");
  6.         TreeNode D = new TreeNode("D");
  7.         TreeNode E = new TreeNode("E", G, null);
  8.         TreeNode B = new TreeNode("B", D, E);
  9.         TreeNode H = new TreeNode("H");
  10.         TreeNode I = new TreeNode("I");
  11.         TreeNode F = new TreeNode("F", H, I);
  12.         TreeNode C = new TreeNode("C", null, F);
  13.         // 构造根节点
  14.         TreeNode root = new TreeNode("A", B, C);
  15.         return root;
  16.     }
  17.     /**
  18.      * 层次遍历
  19.      */
  20.     public void levelOrderVisitTreeNode(TreeNode node) {
  21.         if (null != node) {
  22.             LinkedList<TreeNode> list = new LinkedList<>();
  23.             list.add(node);
  24.             TreeNode currentNode;
  25.             while (!list.isEmpty()) {
  27.                 currentNode = list.poll();
  29.                 System.out.print(currentNode.value);
  31.                 if (null != currentNode.getLeftChildren()) {
  32.                     list.add(currentNode.getLeftChildren());
  33.                 }
  34.                 if (null != currentNode.getRightChildren()) {
  35.                     list.add(currentNode.getRightChildren());
  36.                 }
  37.             }
  38.         }
  39.     }
  41.     public static void main(String[] args) {
  43.         TreeTest treeSearch = new TreeTest();
  44.         TreeNode tree = treeSearch.getTargetTree();
  46.         System.out.print("层次遍历:");
  47.         treeSearch.levelOrderVisitTreeNode(tree);
  48.     }
  49. }