一、三个窗口
命令行窗口
当前文件夹窗
设置当前文件夹
- 在当前文件夹工具栏或当前文件夹窗口中选择某文件夹
使用cd命令
>>cd e:\work
工作区窗口
搜索路径
搜索顺序

设置文件搜索路径使用path命令
>>path(path,'e:\work')用对话框设置文件搜索路径
二、数据类型
整形
- 无符号整数(8位 16位 32位 64位)
- 带符号整数(8位 16位 32位 64位)
```
x=int8(129) x= 127
浮点型
- 单精度(4个字节)
- 双精度(8个字节,matlab默认类型)
```
//single函数 将其他类型转为单精度型
//double函数 将其他类型转换为双精度型
//class函数 查看数据类型
class(4) ans=double
class(single(4)) ans=single
<a name="C0q9D"></a> ## 复型 分为实部和虚部两部分,都默认为双精度型,虚部单位用i或者j来表示6+5i ans= 6.0000+5.0000i 6+5j ans= 6.0000+5.0000i
//real函数,求复数的实部 //image函数,求复数的虚部
<a name="kFOp5"></a>
## 数值数据的输出格式
//format命令的格式:format格式符,只影响输出格式,不影响数据的计算和存储
format long 50/3 ans = 16.666666666666668
常用数学函数
函数的调用格式
- 函数名(函数自变量的值)
- 函数的自变量规定为矩阵变量,也可以是标量(标量本身是矩阵的一种特例)
函数在运算时是函数逐项作用于矩阵的每个元素上,所以最后运算的结果就是一个与自变量同型的矩阵
//函数名(函数自变量的值) >>A=[4,2;3,6] A= 4 2 3 6 >>B=exp(A) //求自然指数 B= 54.5982 7.3891 20.0855 403.4288常用函数的应用
三角函数有以弧度为单位的函数和以角度为单位的函数(以角度为单位的函数在函数名后加“d”)
>>sin(pi/2) ans = 1 >>sind(90) ans = 1abs函数,求实数的绝对值、复数的模、字符串的ASCII码值
>>abs(-4) ans = 4 >>abs(3+4i) ans = 5 >>abs('a') ans = 97用于取整的函数有fix、floor、ceil、round ``` //round函数按照四舍五入的规则取整 //ceil函数是向上取整,取大于等于这个数的第一个整数 //floor函数向下取整,取小于等于这个数的第一个整数 //fix函数是固定取靠近0的整数,即舍去小数取整
round(4.7) ans = 5
floor(3.6) ans = 3
fix(-3.2) ans = -3
ceil(-3.8) ans = -3
<a name="Jp7MW"></a> ### 函数应用举例//求一个三位正整数的个位、十位、百位数字 //rem 求余数 m=345; m1 = rem(m,10) m1 = 5 m2=rem(fix(m/10),10) m2 = 4 m3=fix(m/100) m3 = 3
``` //求[1,100]区间的所有素数 //insprime(n)函数,判断n是否为素数,是返回1,不是返回0 x=1:100; k=insprime(x); //返回的k是标量 k1=find(k); p=x(k1) p= 1至15列 2 3 5 7 11 13 17 19 23 29 31 41 43 47 16至25列 53 59 61 71 73 79 83 89 97三、变量及其操作
赋值语句
- 变量本质是内存单元的一个抽象
- 变量名以字母开头,后接字母、数字或下划线的字符序列
- 变量名区分大小写
- 标准函数名以及命令名必须用小写字母
- 赋值语句两种格式(变量=表达式 表达式)

>>x=sqrt(7)-2i;
>>y=exp(pi/2;
>>z=(5+cosd(47))/(1+abs(x-y))
预定义变量
系统本身定义的变量
//ans 默认赋值变量
//i和j代表虚数单位
//pi代表圆周率
//NaN代表非数
变量的管理
内存变量的删除和修改
- 在工作区完成(右击某个变量)
who命令和whos命令
>> who 您的变量为 a b c d >>whos Name Size Bytes Class Attributes a 1*1 8 double b 1*1 8 double c 1*1 16 double complex d 2*3 48 double内存变量文件
用于保存matlab工作区变量的文件,扩展名为.mat,也叫MAT文件
- save命令:创建内存变量文件
load命令:装入内存变量文件
>> save mydata a x >> load mydata四、MATLAB矩阵的表示
矩阵的建立
直接输入建立矩阵
将矩阵的元素用中括号括起来,按矩阵行的顺序输入各个元素,同一行各元素用逗号或者空格分隔,不同行元素用分号分隔
>> A=[1,2,3;4,5,6;7,8,9] A= 1 2 3 4 5 6 7 8 9利用已建立好的矩阵建立更大的矩阵
>> A=[1,2,3;4,5,6;7,8,9]; >> B=[-1,-2,-3;-4,-5,-6;-7,-8,-9] >> C=[A,B;B,A]可以用实部矩阵和虚部矩阵构成复数矩阵
>> B=[1,2,3;4,5,6]; >> C=[6,7,8;9,10,11]; >> A=B+i*C A = 1.0000+6.0000i 2.0000+7.0000i 3.0000+8.0000i 4.0000+9.0000i 5.0000+10.0000i 6.0000+11.0000i冒号表达式
格式
e1(初始值):e2(步长):e3(终止值)>> t=0:1:5 t = 0 1 2 3 4 5 //若省略e2,则步长为1linspace函数
//linspace(a,b,n) 即(第一个元素,最后一个元素,元素总数) >>x=linspace(0,pi,6) x= 0 0.6283 1.2566 1.8850 2.5133 3.1416结构矩阵和单元矩阵
结构矩阵
//格式: 结构矩阵元素.成员名=表达式 >>a(1).x1=10;a(1).x2='liu';a(1).x3=[11,21;34,78];单元矩阵
建立单元矩阵和一般矩阵相似,直接输入,单元矩阵元素用大括号括起来>> b={10,'liu',[11,21;34,78];12,'wang',[34,191;27,578];... 14,'cai,[13.890;67,23\]} b = [10] 'liu' [2*2 double] [12] 'wang' [2*2 double] [14] 'cai' [2*2 double]五、矩阵元素的引用
通过下标来引用矩阵的元素
>>A=[1,2,3;4,5,6]; >>A(4,5)=10 A = 1 2 3 0 0 4 5 6 0 0 0 0 0 0 0 0 0 0 0 10通过序号来引用
- 在matlab中,矩阵元素按列存储,即首先存储矩阵第一列元素,然后存储第二列元素·······
矩阵元素的序号就是矩阵元素在内存中的排列顺序
>>A=[1,2,3;4,5,6] A= 1 2 3 4 5 6 >>A(3) ans = 2矩阵元素的序号与下标可以利用sub2ind和ind2sub函数实现相互转换
//sub2ind函数:将矩阵中指定元素的行、列下标转换成存储的序号 //格式:D=sub2ind(S,I,J) 即(行数和列数组成的向量,转换矩阵元素的行下标,转换矩阵元素的列下标) >>A=[1:3;4:6] A = 1 2 3 4 5 6 >>D=sub2ind(size(A),[1,2;2,2],[1,1;3,2]) D = 1 2 6 4//ind2sub函数:将矩阵元素的序号转换为对应下标 //格式:[I,J]=ind2sub(S,D) I:行下标 J:列下标 S:行数和列数组成的向量 D:序号 >>[I,J]=ind2sub[3,3],[1,3,5] I= 1 3 2 J= 1 1 2利用冒号表达式获得子矩阵
- A(i:) 第i行的全部元素
- A(:j) 第j列的全部元素
- A(i:i+m,k:k+m) 第i~i+m行内且在第k~k+m列中的所有元素
- A(i:i+m,:) 第i~i+m行的全部元素
>>A=[1,2,3,4,5;6,7,8,9,10;11,12,13,14,15] A= 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 >> A(1:2,:) ans= 1 2 3 4 5 6 7 8 9 10 >> A(2:3,1:2:5) ans= 6 8 10 11 13 15利用空矩阵删除矩阵的元素

改变矩阵的形状
//reshape(A,m,n):在矩阵总元素保持不变的前提下,将矩阵A重新排成m*n的二维矩阵 >> x=[1,2,3,4] >>y=reshape(x,2,2) y = 1 3 2 4//A(:):将矩阵A的每一列元素堆叠起来,成为一个列向量 >>A=[1,2;3,4] A= 1 2 3 4 >>B=A(:) B= 1 3 2 4六、基本运算
算数运算
基本算数运算
- 基本算数运算符:+、-、*、/(右除)、\(左除)、^(乘方)
- matlab的算数运算是在矩阵意义下进行的
- 单个数据的算数运算只是矩阵运算的一种特例
- 矩阵B/A,即Binv(A) A\B,即inv(A)B
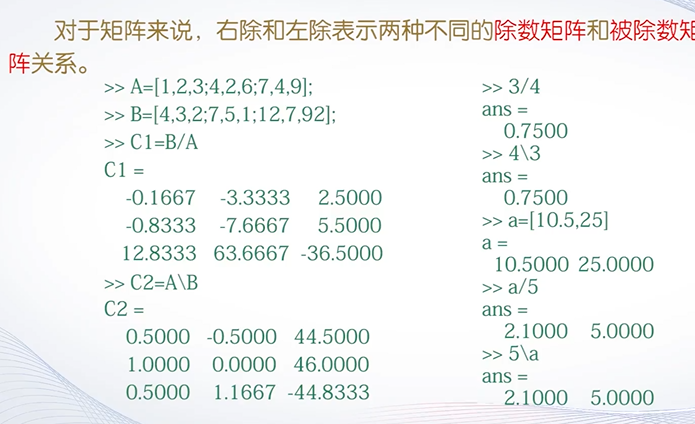

- 点运算
- 点运算符:.* ./ .\ .^
-
关系运算
关系运算符:< <= > >= == ~=(不等于)
- 两个标量,直接比较
- 两个矩阵,必须同型,每个元素逐个比较,最终输出与其同型的关系矩阵
- 一个标量,一个矩阵,把标量和矩阵元素逐一比较,输出与其同型的关系矩阵
逻辑运算
- 逻辑运算符:& | ~
- 算数运算优先级最高,逻辑运算优先级最低
逻辑非运算是单目运算,优先级比双目运算高
//水仙花数 >>m=100:999; >>m1=rem(m,10); >>m2=rem(fix(m/10),10); >>m3=fix(m/100); >>k=find(m==m1.*m1.*m1+m2.*m2.*m2+m3.*m3.*m3) k= 54 271 272 308 >>s=m(k) s= 153 370 371 407七、字符串处理
字符串的表示
单引号括起来的字符序列
>>xm='hello' >>xm(1:3) ans= hel若字符串中字符含有单引号,则该单引号字符要用两个单引号表示
>>'I''m a student' ans = I'm a student建立多行字符串,形成字符串矩阵
>>ch=['abcdef';'123456']; >>ch(2,3) ans = 3一些操作 ``` //取第1~5个字符组成的子字符串 //将字符串倒过来重新排列 //将字符串中小写变大写 //统计字符串中小写字母个数
ch=’ABc123d4e56Fg9’; subch=ch(1:5) subch= ABc12
revch=ch(end:-1:1) revch = 9gF65e4d321cBA
k=find(ch>=’a’&ch<=’z’) k = 3 7 9 13
ch(k)=ch(k)-(‘a’-‘A’) ch= ABC123D4E56FG9
length(k) ans = 4
<a name="NemNZ"></a> ## 字符串的操作 <a name="d2aDL"></a> ### 字符串的执行//格式:eval(s) t=pi; m=’[t,sin(t),cos(t)]’; y=eval(m) y= 3.1416 0.0000 -1.0000 ```
字符串与数值之间的转换
- abs和double函数都可以用来获取字符串矩阵所对应的ASCII码数值矩阵
- char函数可以把ASCII码矩阵转换为字符串矩阵
>>s1='MATLAB'; >>a=abs(s1); a= 77 65 84 76 65 66 >>char(a+32) ans= matlab字符串的比较
- 利用关系运算符
- 两个字符串里的每个字符依次按ASCII值大小逐个进行比较,比较的结果是一个数值向量,其中元素要么是1,要么是0
>>'www0'>='W123' ans = 1 1 1 0
- 利用字符串比较函数
- strcmp(s1,s2):用来比较字符串s1和s2是否相等,相等返回1,不相等返回0
- strncmp(s1,s2,n):用来比较两个字符串前n个字符是否相等,相等返回1,否则返回0
- strcmpi(s1,s2):忽略大小写,比较两者是否相等
strncmpis(s1,s2,n):忽略大小写,比较前n个字符是否相等
字符串的查找与替换
findstr(s1,s2):返回短字符串在长字符串中的开始位置
- strrep(s1,s2,s3):将字符串s1中的所有子字符串s2替换为字符串s3
```
p=findstr(‘This is a test!’,’is’) p= 3 6 //空格也是一个字符
result=strrep(‘This is a test!’,’test’,’class’) result= This is a class! ```


