一、数值微分和数值积分

数值微分

数值差分与差商

image.png
image.png

数值微分的实现

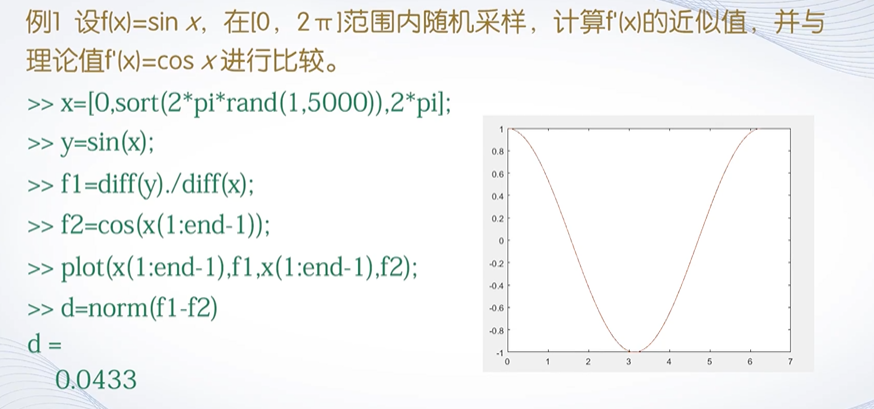
  • diff()函数

image.png
image.png

数值积分

  • [l,n]=quad(filename,a,b,tol,trace)

image.png
image.png

  • intergral()函数

image.png
image.png

  • quadgk（）函数

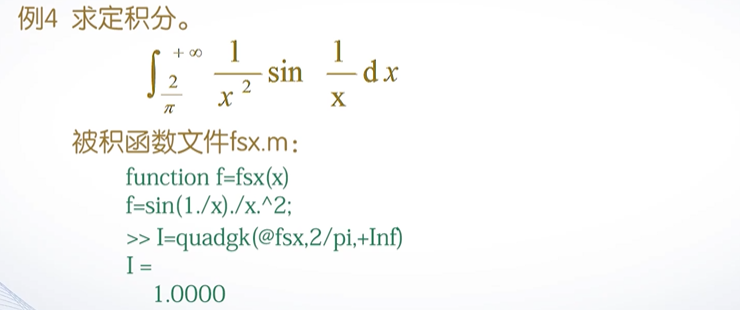
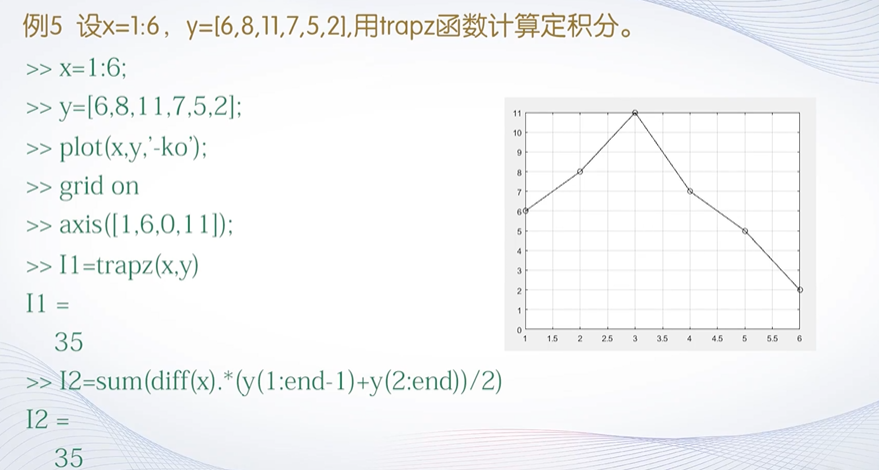
image.png
image.png

  • trapz（）函数

image.png
image.png
image.png

  • 多重积分

image.png
image.png

二、线性方程组求解

直接法

  1. 高斯消去法
  2. 列主元消去法
  3. 矩阵的三角分辨法
  • 利用左除运算符的直接解法
  • Ax=b 即x=A\b 如果矩阵A奇异或接近奇异，会给出警告信息

    利用矩阵分解求解线性方程组

  1. LU分解
  2. QR分解
  3. Cholesky分解

image.png

迭代解法

image.png
image.png
image.png
image.png
image.png
image.png
image.png

三、非线性方程求解

单变量非线性方程求解

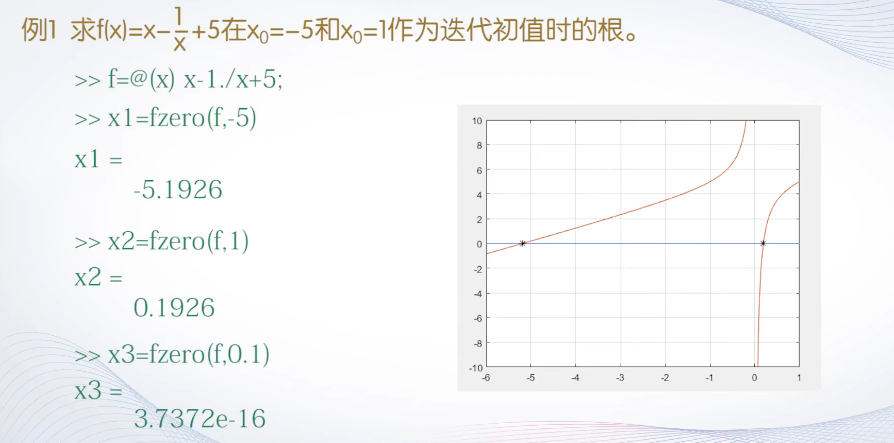
  • x=fzero(filename,x0) filename 待求根方程左端的函数表达式 x0初始值

image.png

非线性方程组求解

  • x=fsolve(filename,x0,option)
  • x 返回的近似解， filename 待求根方程左端的函数表达式，x0为初值，option用于设置优化工具箱的优化参数，可调用optimset函数完成

image.png
image.png

函数极值的计算

无约束最优化问题

  • 求最小值的函数
  • [xmin,fmin]=fminbnd(filename,x1,x2,option)
  • [xmin,fmin]=fminsearch(filename,x0,option)
  • [xmin,fmin]=fminunc(filename,x0,option)
  • filename是定义的目标函数，第一个函数的输入变量x1，x2分别表示研究区间的左右边界。
  • 后两个函数的输入变量x0是一个向量，表示极值点的初值。
  • option为优化参数，可以通过optimset函数来设置

image.png

有约束最优化问题

image.png
image.png
image.png

常微分方程数值求解

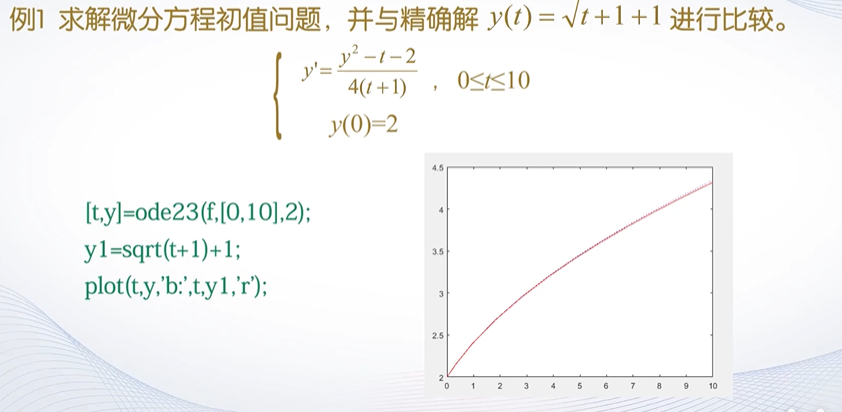
  1. [t,y]=solver(filename,tspan,y0,option)
  • t,y分别给出时间向量和相应的数值解
  • solver为求常微分方程数值解的函数
  • filename是定义f(t,y)的函数名，该函数必须返回一个列向量
  • tspan形式为[t0,tf]，表示求解区间
  • y0是初始状态向量
  • option是可选参数，用于设置求解属性
  1. 常微分方程数值求解函数的统一命名格式
  • odennxx
  • ode ordinary differential equation
  • nn 数字，代表 所用方法的阶数
  • xx 字母，用于标注方法的专门特征

image.png
image.png
image.png

刚性问题

  • 有一类常微分方程，其解的分量有的变化很快，有的变化很慢，且相差悬殊，即刚性问题

image.png
image.png
image.png

  • tic 保存当前时间
  • toc 语句完成时间

image.png

常微分方程应用举例

Lotka-Volterra模型链接