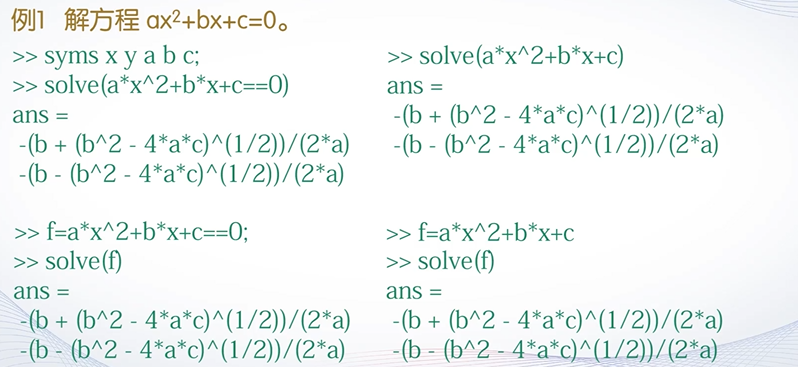一、符号对象

建立

sym函数

  • 用于建立单个符号对象
  • 调用格式：符号对象名=sym(A)
  • A 建立符号对象 可以是一个数值常量、数值矩阵或数值表达式（不加单引号），此时符号对象为一个符号常量
  • A也可以是一个变量名（加单引号），这时符号对象为一个符号变量 ``` //符号常量

    t=sym(2); t+1/2 ans= 5/2 sin(sym(pi/3)) ans= 3^(1/2)/2 //二分之根号三 sin(pi/3) ans=0.8660

//符号变量

a=g; b=-8; x=sym(‘a’); y=sym(‘b’); w=(a+b)(a-b) w= -39 s=(x+y)(x-y) s= (a+b)*(a-b) //符号计算的结果是一个精确的数学表达式 //数值计算的结果是一个数值 ```

syms命令

  • 可以一次定义多个符号变量
  • 一般调用格式：syms 符号变量名1 符号变量名2 ···符号变量名n

  • 变量名不能加单引号，相互之间用空格隔开

    符号对象的运算

    四则运算

        • / ^

  • 运算结果是符号表达式

    1. >>syms x;
    2. >>f=2*x^2+3*x-5;
    3. >>g=x^2-x+7;
    4. >>f+g
    5. ans=
    6.    3*x^2+2*x+2

    关系运算

  • < <= > >= == ~=

  • 对应的函数：lt()、le()、gt()、ge()、eq()、ne()
  • 若参与运算的是符号表达式，其结果是一个符号关系表达式
  • 若参与运算的是符号矩阵，其结果是由符号关系表达式组成的矩阵
  • 在进行符号对象的运算前，可用assume函数对符号对象设置值域
  • assume(condition)
  • assume(expr,set)
  • 第一种格式指定变量满足条件condition 第二种格式指定表达式expr属于集合set ```

    syms x; assume(x<0); abs(x)==x ans= -x==x

assume(x,’positive’) abs(x)==x ans= x==x ```

逻辑运算

  • 三种逻辑运算符：& | ~
  • 四个逻辑运算函数：and（） or（） not（0 xor（） ```

    syms x; y=x>0&x<10 y= 0<x&x<10

y=and(x>0,x<10) y= 0

因式分解与展开运算

  • factor(s)：对符号表达式s分解因式
  • expand(s)：对符号表达式s进行展开
  • collect(s)：对符号表达式s合并同类项

  • collect(s,v)：对符号表达式s按变量v合并同类项

    >>syms a b;
>>s=a^3-b^3;
>>factor(s)
ans=
  [a-b,a^2+a*b+b^2]

    梅森素数

    image.png

    其他

  • 提取有理式分式的分子分母：[n,d]=numden(s)

  • 提取符号表达式的系数：c=coeffs(s,x)
  • 符号表达式化简：simplify(s)
  • 符号多项式与多项式系数向量之间的转换
  • 符号多项式与多项式系数向量之间的转换
  • 符号多项式转换为多项式系数向量：p=sym2poly(s)
  • 多项式系数向量转换为符号多项式：s=poly2sym(p)

image.png

符号运算中变量的确定

  • 没有确定指明自变量时，有两个原则：1）寻找除i,j之外，在字母顺序上最接近x的小写字母。2）若表达式中有两个符号变量与x的距离相等，则AXCII码大者优先
  • symvar()函数可以用于查找一个符号表达式中的符号变量
  • symvar(s,n) 返回符号表达式s中的n个符号变量

  • symvar(s,1)查找表达式s的主变量

    符号矩阵

  • 函数作用于符号矩阵时，是分别作用于矩阵的每一个元素

  • 矩阵运算依旧适合

image.png

二、符号微积分

符号函数的极限

limit命令

  • 调用格式：limit(f,x,a) 即函数f关于变量x，在a点的极限。
  • 若x省略，采用系统默认的自变量，a的默认值为0

  • limit(f,x,a,’right’) limit(f,x,a,’left’) 单边极限

    符号函数的导数

    diff命令

  • diff(f,x,n) 函数f关于变量x的n阶导数 n默认为1

    符号函数的积分

    int命令

  • int(f,x) 函数f对变量x的不定积分

  • int(f,x,a,b) 定积分，a，b分别为上限和下限
  • 当函数f关于变量x在区间[a,b]可积时，函数返回一个定积分结果
  • 当a，b中有一个是inf时，函数返回一个广义积分

  • 当a，b中有一个符号表达式时，函数返回一个符号函数

    河道水流量估计问题

    image.png

    xi=0:50:600    //建立横坐标向量
yi=[4,4,4.5,4.6,4.8,4.9,5.1,5.4,5.2,5.5,4.9,4.8,4.7]   //建立水流深度向量
p=polyfit(xi,yi,3)  //曲线拟合
plot(xi,yi,'o',xi,polyval(p,xi),'r');  //绘图
syms y x；
y=poly2sym(p,x);  //多项式向量转换为符号表达式
s=int(y,x,0,600);   //计算横截面积
v=s*0.6;   //计算水流量
eval(v)   //转换为数值形式

    三、级数

    级数求和

  • sum() 可以进行级数求和，但是当项数多时，不好用

  • 求无穷级数的和需要符号表达式求和函数symsum()
  • 调用格式：symsum(s,v,n.m)
  • s 级数的通项，是一个符号表达式 v 求和变量，省略时，使用系统的默认变量

  • n，m求和变量v的初值和末值

    泰勒级数

  • Taylor(f,v,a,Name,Value) 将f按变量v在a点展开为泰勒级数，v省略时按默认规则确定变量，a的默认值是0

  • Name和Value为选项设置，经常成对使用，前面为选项名。后者为该选项的值

  • Name有三个取值 ‘ExpansionPoint’（指定展开点，对应只可以是标量或向量，未设置时，展开点为0） ‘Order’（指定截断参数。对应值为一个正整数，未设置时，截断参数为6，即展开式最高阶为5） ‘OrderMode’（指定展开式采用绝对阶或相对阶，对应值为’Absolute’或’Relative’。未设置时取’Absolute’

    复杂函数计算问题

    image.png

    四、符号方程求解

    代数方程符号求解

    solve(s)函数

  • 求解用符号表达式表示的代数方程

  • solve(s)：求解符号表达式s的代数方程，求解变量为默认变量
  • solve(s,v)：求解符号表达式s的代数方程，求解变量为v
  • solve(s1,s2,···,sn,v1,v2,···,vn)：求解符号表达式s1，s2，···，sn组成的代数方程组，求解变量分别为v1，v2，···，vn

image.png

常微分方程符号求解

  • matlab中，D表示导数
  • Dy表示y的一阶导，D2y表示y的二阶导
  • Dy(0)=5 表示在0处，y的一阶导为5
  • 符号常微分方程求解可以通过函数dsolve来实现
  • dsolve(e,c,v) 用于求解常微分方程e在初值条件c下的特解。 v是方程中的自变量，省略时按默认原则处理，若没有给出初值条件c，则求方程的通解
  • dsolve(e1,e2,···,en,c1,c2,···,cn,v)
  • 用于求解常微分方程组e1,e2···en在初值条件c1,c2,···cn下的特解，若不给出初值条件，则求方程组通解。v给出求解变量，如果没有指定自变量，则采用默认自变量t