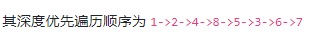一、稀疏矩阵
1、上三角矩阵
在矩阵中,下标分别为i 和 j 的元素,对应的一维数组下标计算公式:(2n-i+1)x i/2+j
2、下三角矩阵
二、顺序表和链表
三、顺序存储和链式存储
四、队列和栈
1、队列:先进先出
2、栈:先进后出
3、循环队列
队空条件:head=tail
队满条件:(tail+1)%size = head
栈和队列的例题
双端队列,两端进入、只能从一端输出,若有e1、e2、e3、e4依次进入双端队列,则得不到输出序列
————————————————————-
————>
<———- <———
—————————————————————
A .e4.e3.e2.e1
B. e4.e2.e1.e3
C. e4.e3.e1.e2
D. e4.e2.e3.e1
分析:
A:e1.e2.e3.e4 —->
B:e1.e2 —->
e3 <—-
e4 —->
C: e1.e2 <——
e3.e4 ——>
D:e1 <——
e2 ——>
e3 进不去了
五、广义表
1、定义
是n个表元素组成的有限序列,是线性表的推广
通常用递归的方式进行定义,记做:LS = (a0,a1,…an)
1)其中Ls是表名,ai是元素,可以是子表也可以是数据元素
2)n是广义表长度
3)n=0 为空表
4)深度:包含括号的重数,空表深度为1
5)基本运算 :
取表头 head(Ls)
取表尾 tail(Ls)
6)例1:
LS1= (a, (b,c) , (d,e) )
head (LS1)= a
tail(LS1) = ( (b,c) , (d,e) )
7)例2:
6)中的深度和长度为?
深度:2
长度:3
8)例3:
6)中将其的b字母取出,应该怎么操作
tail(Ls1) = ( (b,c) , (d,e) ) = LS2
head(LS2) = (b,c) = LS3
head(LS3) = b
六、树和二叉树
1、节点的度:分支数
2、树的度:最大的分支数
3、分支结点
4、内部结点:除了根和叶子节点
七、满二叉树与完全二叉树
1、满二叉树
2、完全二叉树
除了最后一层,其他层的节点都是满的,且最后一层,从左到右依次有节点,才是完全二叉树
3、非完全二叉树
4、二叉树性质:
1)二叉树第 i 层上,最多有 2^(i-1) 个节点
2)深度为k的二叉树,最多有2^k - 1 个节点
3)对于任何一颗二叉树,如果其叶子节点数 为 n0 , 度为2的节点数为 n2, 那么 n0 = n2+1
4)对于一颗有n个节点的完全二叉树,节点按层序编号,每层从左到右,对于任一节点i ,有:
如果i = 1,则节点i 无父节点,是二叉树的根;
如果i > 1,则父节点是 i/2 向下取整
如果 2i >n,则结点无叶子节点,无左子节点,否则,其左子节点为 2i
如果 2i+1>n,则节点无右子节点,否则其右子节点为2i+1
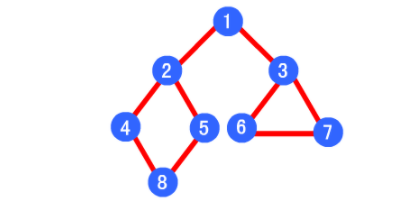
八、二叉树遍历
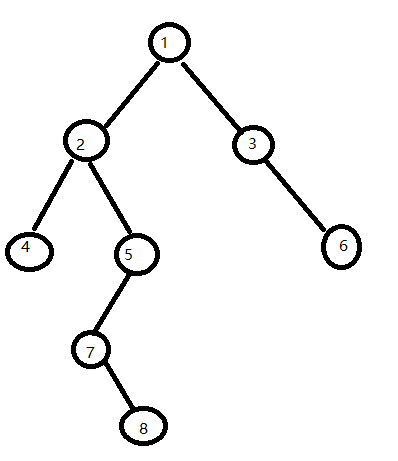
1、层级遍历
2、前序遍历(根左右)
3、中序遍历(左根右)
4、后序遍历(左右根)
48752631
九、反向构造二叉树
1、由前序序列ABHFDECG,中序 序列 HBEDFAGC构造二叉树
1)由前序可以确定 A是根
2)有中序可以确定,根的左子树为 HBEDF ,右边GC
3)由前序可以确定 ,B是左子树的根,则 H,EDF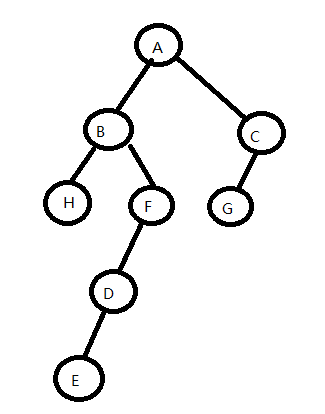
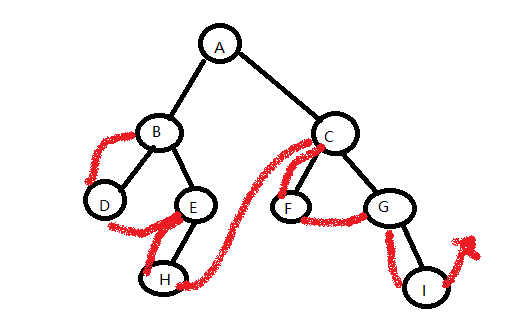
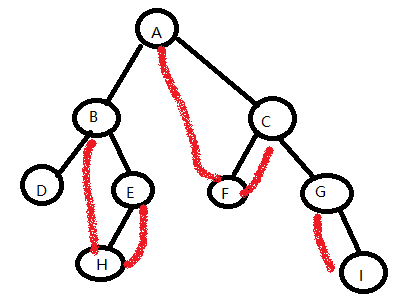
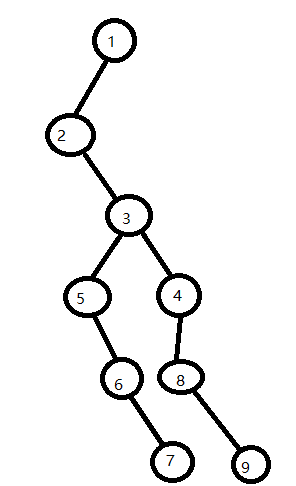
十、树转二叉树
1、孩子节点-左子树节点
2、兄弟节点-右子树节点
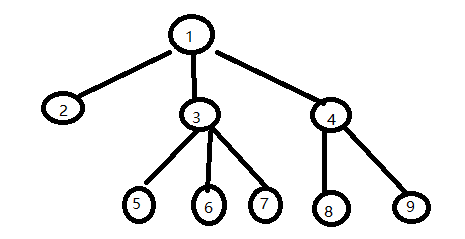
方法一理论分析:
1)对于节点1,没有兄弟节点,有孩子节点 2、3、4,以最左边的孩子节点,当其左节点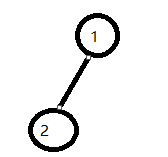
2)对于节点2,没有孩子节点,有兄弟节点 3、4,以最左边兄弟及诶但,当右节点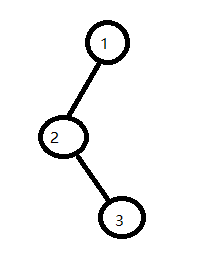
3)对于节点3,有孩子节点,有兄弟节点,5是左,4是右
…
方法二连线:
1)将所有的兄弟节点相连,除了最左边的线,其他线去掉,然后旋转,得到结果(新连线都是右子树)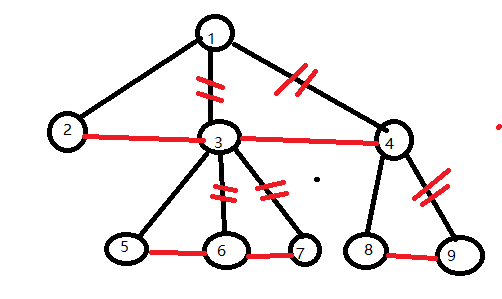
十一、查找二叉树
1、定义
所有的左子树小于根节点,所有右子树大于根节点,又叫排序二叉树
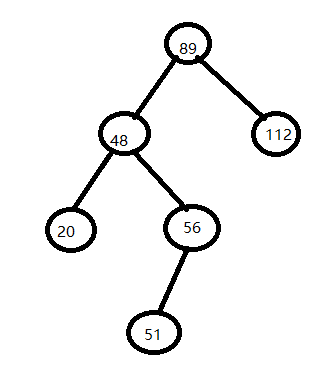
2、插入节点
1)若该键值节点已经存在,则不插入,如48
2)若查找二叉树为空树,则以新节点为查找二叉树
3)与根节点比较,小的是左子树,大的是右子树
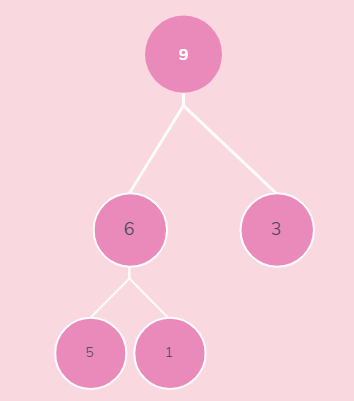
3、删除节点
1)若待删除的节点是叶子节点,直接删除
2)若待删除的节点只有一个子节点,则将这个子节点与待删除的节点的父节点直接相连
比如 删除 56,直接把51 和 48相连
3)若删除的节点P有两个子节点,则在其左子树上,用中序遍历寻找关键值最大的节点S,
用节点S的值代替节点P的值,然后删除S,删除S后,子节点操作如1)2)
比如删除89,查找到最大值是56,那么就把 89位置用 56代替,然后51 跟48相连
十二、最优二叉树(哈夫曼树)
1、树的路径长度:树的分支数
2、权
3、带权路径长度
4、树的带权路径长度(树的代价)
所以叶子节点的带权路径长度 加和
例题
假设有一组权值:
5、29、7、8、14、23、3、11
构造哈夫曼树
1) 首先选出两个最小权值的节点,5、3
2)两数相加,次数 数据为 8、29、7、8、14、23、11
3)根据2)的找出最小的两个数为 8.7
4)15、29、8、14、23、11 —— 》8,11
….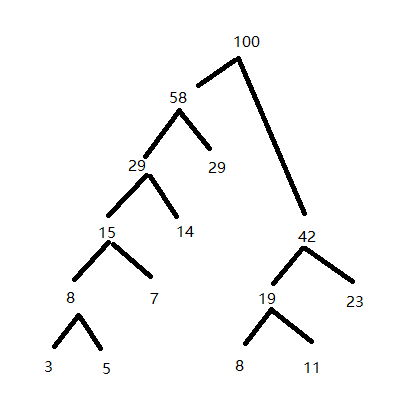
带权路径长度:
3x5 + 5x5 +7x4 + 14x3+ 29x2+8x3+11x3+23x2
十二、线索二叉树
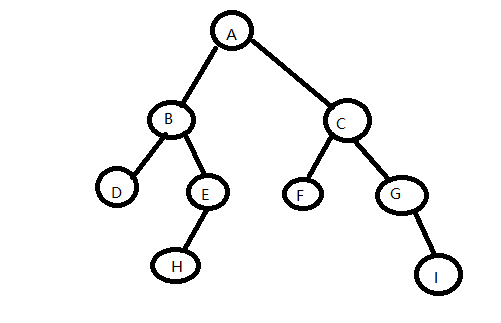
1、前序线索二叉树
2、中序线索二叉树
3、后序线索二叉树
DHEBFIGCA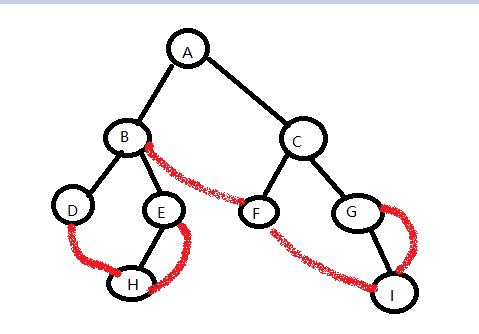
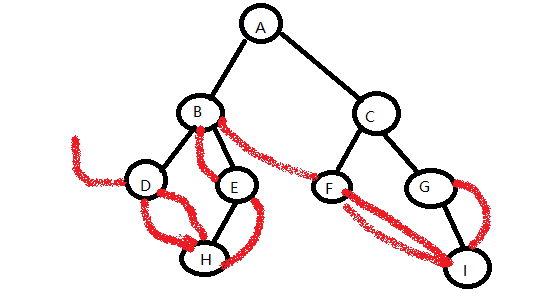
十二、平衡二叉树
1、定义
1)任意节点的左右子树深度相差不超过1
2)每结点的平衡度只能为 -1、0或1
十三、图
1、无向图
2、有向图
3、完全图
4、邻接矩阵
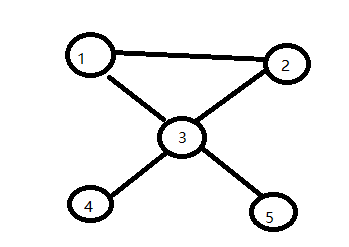
1 2 3 4 5
1 0 1 1 0 0
2 1 0 1 0 0
3 1 1 0 1 1
4 0 0 1 0 0
5 0 0 1 0 0
5、邻接表
每个顶点的邻接顶点用 链表连接,用一维数组 顺序存储每个链表的头指针
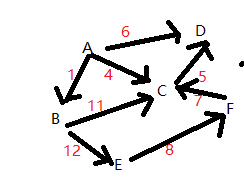
A —->B|1 ——>C|4 —-> D|6
B —->C|11 ——>E|12
C —->D|5
D
E —->F|8
F —->C|7
十四、图的遍历
1、深度优先
2、广度优先
十五、图的拓扑排序
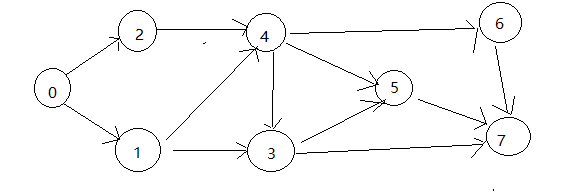
01243567
01246357
02143567
02143657
1)找入度为0的节点,当归到排序中后,砍掉节点和相关的线
十六、图的最小生成树
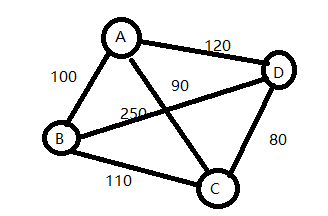
不能形成环路
方法一:普利姆
1)从A开始,出去的线 有100、90、120 ,最短的线是 90, A—C ,C 被纳入
2)再看,从A和C出发的线,最短的是哪条,80,则找到D ,C—D
3)再看,从A\C\D出发的线,最短的是哪条,100,则A —B
方法二:克鲁斯卡尔
1)4个顶点,3条边。
2)找最小的边,80,C—D
3)再找一条最小的边,90,A—C
4)再找一条最小的变,100,A—B
十七、算法的特性
1、有穷性
2、确定性,我输入1得到是2,再次输入1,得到的是3,这不是确定性
3、输入个数>=0
4、输出个数>=1
5、有效性,如果a=0,b/a就无效
十八、算法复杂度
1、时间复杂度
O(1) < O(logn) < O(n)
2、空间复杂度
十九、顺序查找与二分查找
1、顺序查找
平均查找长度 :ASL = (n+….+2+1)/n= (n+1)/2
时间复杂度 :o(n)
2、二分查找
平均查找长度 :ASL = 每个节点的查找次数/所有节点数
时间复杂度 : o(log2n)
具体内容见子文章:二分查找
参考文章:
https://blog.csdn.net/chengmo123/article/details/89257230
https://blog.csdn.net/weixin_43896318/article/details/105832557
二十、直接插入排序
1)每一个新元素和数列是倒着比的
2)时间复杂度 o(n2)
| 25 | 34 | 48 | 41 | 87 | 73 | 98 | 102 | 次数 | 比较过程 |
|---|---|---|---|---|---|---|---|---|---|
| 25 | 0 | 初始 | |||||||
| 25 | 34 | 1 | 34与25比较,比25大,插入到后面 | ||||||
| 25 | 34 | 48 | 1 | 48与34比较,比34大,插入到后面 | |||||
| 25 | 34 | 41 | 48 | 2 | 41与48比较,比48小; 41与34比较,比34大,插入到34后面 |
||||
| 25 | 34 | 41 | 48 | 87 | 1 | 87与48比较,比48大,插入到48后面 | |||
| 25 | 34 | 41 | 48 | 73 | 87 | 2 | 73与87比较,比87小; 73与48比较,比48大,插入到48后面 |
||
| 25 | 34 | 41 | 48 | 73 | 87 | 98 | 1 | 98与87比较,比87大,插入到87后面 | |
| 25 | 34 | 41 | 48 | 73 | 87 | 98 | 102 | 1 | 102与98比较,比98大,插入到98后面 |
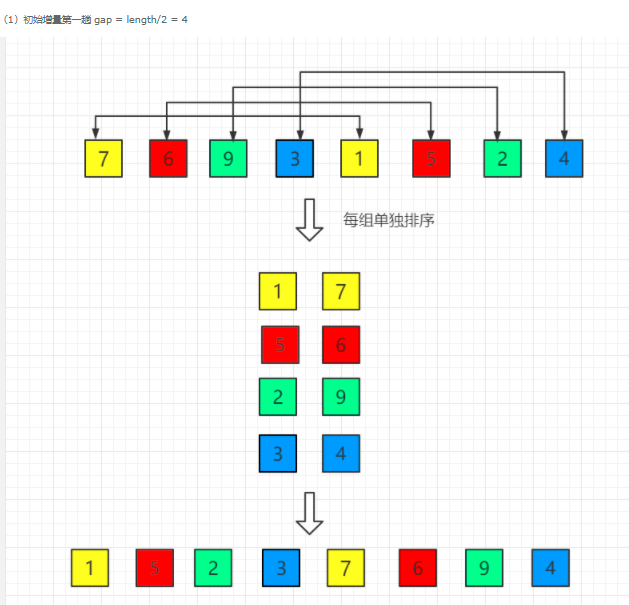
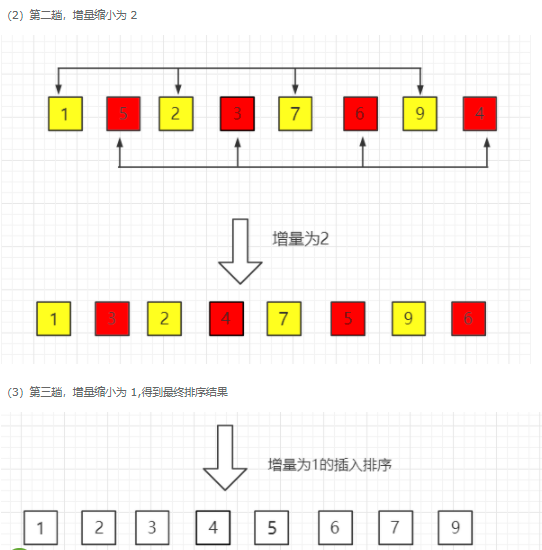
二十一、希尔排序
1)针对直接插入排序算法的改进
2)希尔排序又称缩小增量排序
3)时间复杂度 O(n^(1.3-2))
4)对中等大小规模表现良好,但对规模非常大的数据排序不是最优选择,总之比一般 O(n^2 ) 复杂度的算法快得多
例子1
- 首先对原始序列分组,d = 8/2 = 4 | 25 | 34 | 48 | 41 | 87 | 73 | 98 | 102 | | —- | —- | —- | —- | —- | —- | —- | —- |
== >> 颜色相同为一组,组内进行直接插入排序,得比较次数为 4
| 25 | 87 |
|---|---|
| 34 | 73 |
|---|---|
| 48 | 98 |
|---|---|
| 41 | 102 |
|---|---|
== >> 缩小增量为 d = d/2 = 2 , 颜色相同为一组,组内进行直接插入排序,比较次数为 4+4 = 8
| 25 | 34 | 48 | 41 | 87 | 73 | 98 | 102 |
|---|---|---|---|---|---|---|---|
| 25 | 48 | 87 | 98 |
|---|---|---|---|
| 34 | 41 | 73 | 102 |
|---|---|---|---|
== >> 缩小增量为 d = d/2 = 1 , 组内进行直接插入排序 , 比较次数 为 9
| 25 | 34 | 48 | 41 | 87 | 73 | 98 | 102 |
|---|---|---|---|---|---|---|---|
例子2
二十二、直接选择排序
1)从待排序序列中,找到最小的元素
2)如果最小元素不是待排序序列的第一个元素,将其和第一个元素互换
3)从余下的 N - 1 个元素中,找出关键字最小的元素,重复(1)、(2)步,直到排序结束
4)无论是最坏情况、最佳情况还是平均情况都需要找到最大值(或最小值),因此其比较次数为n(n-1)/2次,时间复杂度 o(n2)
**
| 82 | 25 | 48 | 41 | 34 | 比较过程 |
|---|---|---|---|---|---|
| 25 | 在原始序列中找到 最小值,25 | ||||
| 25 | 34 | 在剩下的数(82,48,41,34)中找到最小的 | |||
| 25 | 34 | 41 | 在剩下的数(82,48,41)中找到最小的 | ||
| 25 | 34 | 41 | 48 | 在剩下的数(82,48)中找到最小的 | |
| 25 | 34 | 41 | 48 | 82 |
二十三、堆排序
1、大顶堆、小顶堆
堆是具有以下性质的完全二叉树:
每个结点的值都大于或等于其左右孩子结点的值,称为大顶堆;
或者每个结点的值都小于或等于其左右孩子结点的值,称为小顶堆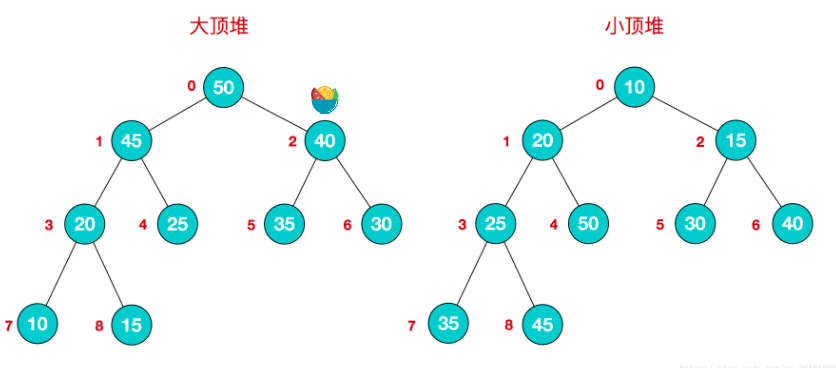
同时,我们对堆中的结点按层进行编号,将这种逻辑结构映射到数组中就是下面这个样子
该数组从逻辑上讲就是一个堆结构,我们用简单的公式来描述一下堆的定义就是:
大顶堆:arr[i] >= arr[2i+1] && arr[i] >= arr[2i+2]
小顶堆:arr[i] <= arr[2i+1] && arr[i] <= arr[2i+2]
2、堆排序的基本思想
1)一般升序采用大顶堆,降序采用小顶堆
2)将无需序列构建成一个堆,根据升序降序需求选择大顶堆或小顶堆;
3)将堆顶元素与末尾元素交换,将最大元素 “沉” 到数组末端;
4) 重新调整结构,使其满足堆定义,然后继续交换堆顶元素与当前末尾元素,反复执行调整 + 交换步骤,直到整个序列有序。
https://blog.csdn.net/qq_36186690/article/details/82505569 https://zhuanlan.zhihu.com/p/128892381
例子1
1、6、3、5、9 堆排序,升序
1)升序-先大顶锥化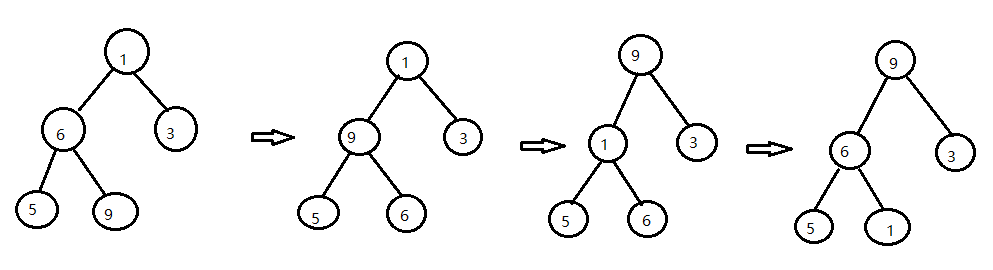
数组:
0 1 2 3 4
1 6 3 5 9
从最后一个节点开始,先与其根节点比较大小,如果比根节点大,相互交换
9—-》6
9—-》1
6—-》1
最终得到大顶锥
2)再取堆顶的元素,放到数组最后一个位置,然后去掉这个最大元素,形成大顶锥
一直重复此过程,直到剩余一个元素,排序完成
- 初始
0 1 2 3 4
9 6 3 5 1
=================》》取栈顶元素 9 ,放在数组 arr[4]位置,9跟1互换后,重新组织大堆栈
0 1 2 3 4
1 6 3 5 9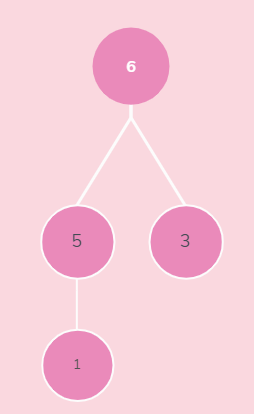
0 1 2 3 4
6 5 3 1 9
=================》》取栈顶元素 6 ,放在数组 arr[3]位置,6跟1互换后,重新组织大堆栈
0 1 2 3 4
1 5 3 6 9
0 1 2 3 4
5 1 3 6 9
=================》》取栈顶元素5,放在数组arr[2]位置,5与3互换后,重新组织大堆栈
0 1 2 3 4
3 1 5 6 9 
0 1 2 3 4
3 1 5 6 9
=================》》取栈顶元素3…
0 1 2 3 4
1 3 5 6 9
二十四、冒泡排序
时间复杂度 o(n2)
把相邻的元素两两进行比较,根据大小交换元素的位置
例子:
5、8、6、3、9、2、1、7
第一轮
5、6、8、3、9、2、1、7
5、6、3、8、9、2、1、7
5、6、3、8、2、9、1、7
5、6、3、8、2、1、9、7
5、6、3、8、2、1、7、9
第二轮
5、3、6、8、2、1、7、9
5、3、6、2、8、1、7、9
5、3、6、2、1、8、7、9
5、3、6、2、1、7、8、9
第三轮
3、5、6、2、1、7、8、9
3、5、2、6、1、7、8、9
3、5、2、1、6、7、8、9
第四轮
3、2、5、1、6、7、8、9
3、2、1、5、6、7、8、9
第五轮
2、3、1、5、6、7、8、9
2、1、3、5、6、7、8、9
第六轮
1、2、3、5、6、7、8、9
二十五、快速排序
快速排序的平均时间复杂度是 O(nlogn),最坏情况下的时间复杂度是 O(n^2)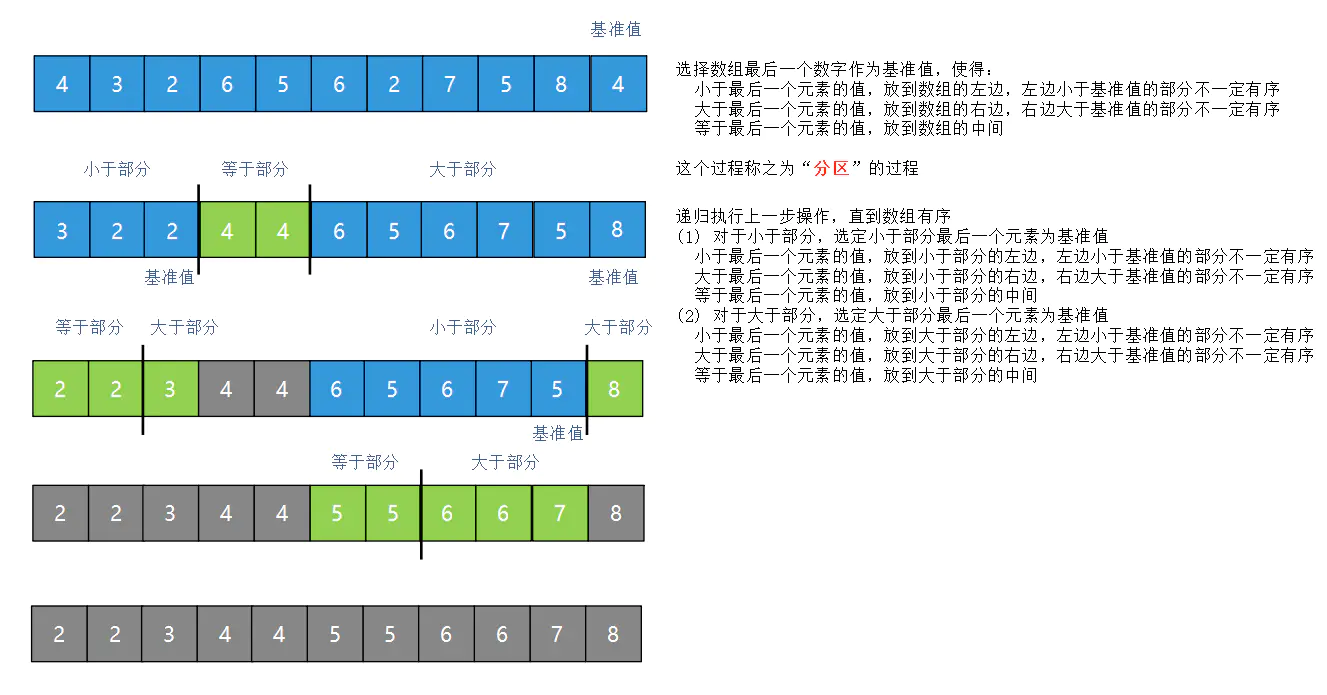
https://www.sohu.com/a/246785807_684445 https://www.jianshu.com/p/a68f72278f8f
二十六、归并排序
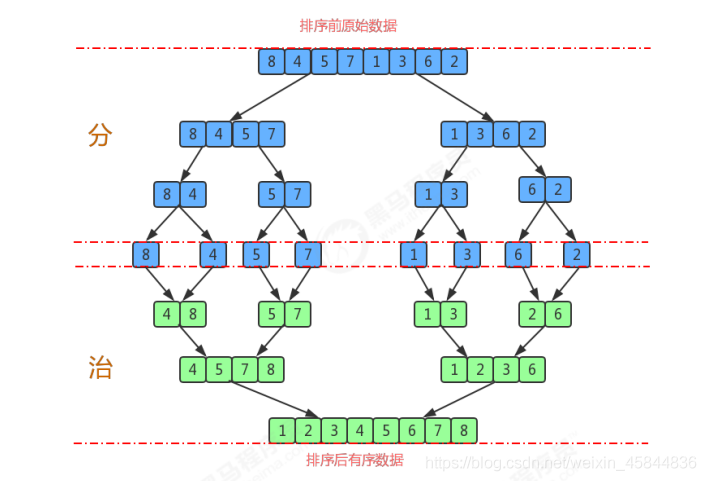
1)
8、4 排序 —》 4、8
5、7 排序 —》 5、7
1、3 排序 —》 1、3
6、2 排序 —》 2、6
2)
4、8、5、7 排序 —》
4、8 5、7
L R 4与5 比较,4小,所以L右移、R不动,得 4 X X X
4、 8 5、7
L R 8与5 比较,5小,所以R右移、L不动,得 4 5 X X
4、 8 5、7
L R 8与7 比较,7小,得 4 5 7 8
1、3、2、6 排序同理得 —》1236
3)4、5、7、8 与 1、2、3、6同理排序
参考:
https://blog.csdn.net/weixin_45844836/article/details/109142733
二十七、基数排序
核心思想是:
1)先找十个桶:0~9
2)第一轮按照元素的个位数排序
桶内分别存放上述数组元素的个位数,按照数组元素的顺序依次存放
之后,按照从左向右,从上到下的顺序依次取出元素,组成新的数组
3)第二列按十位取数
4)第四位按百位取数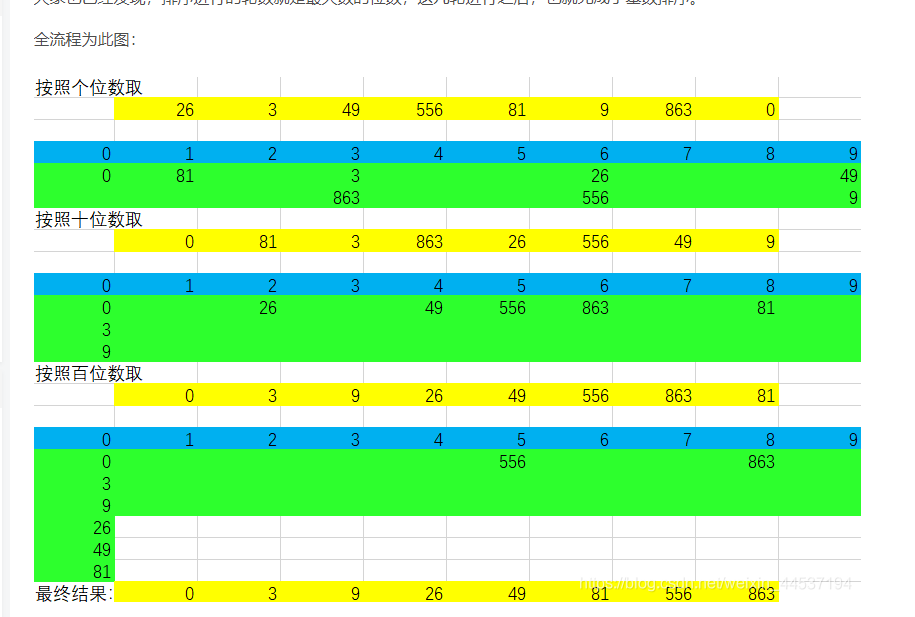
参考:https://blog.csdn.net/weixin_44537194/article/details/87302788