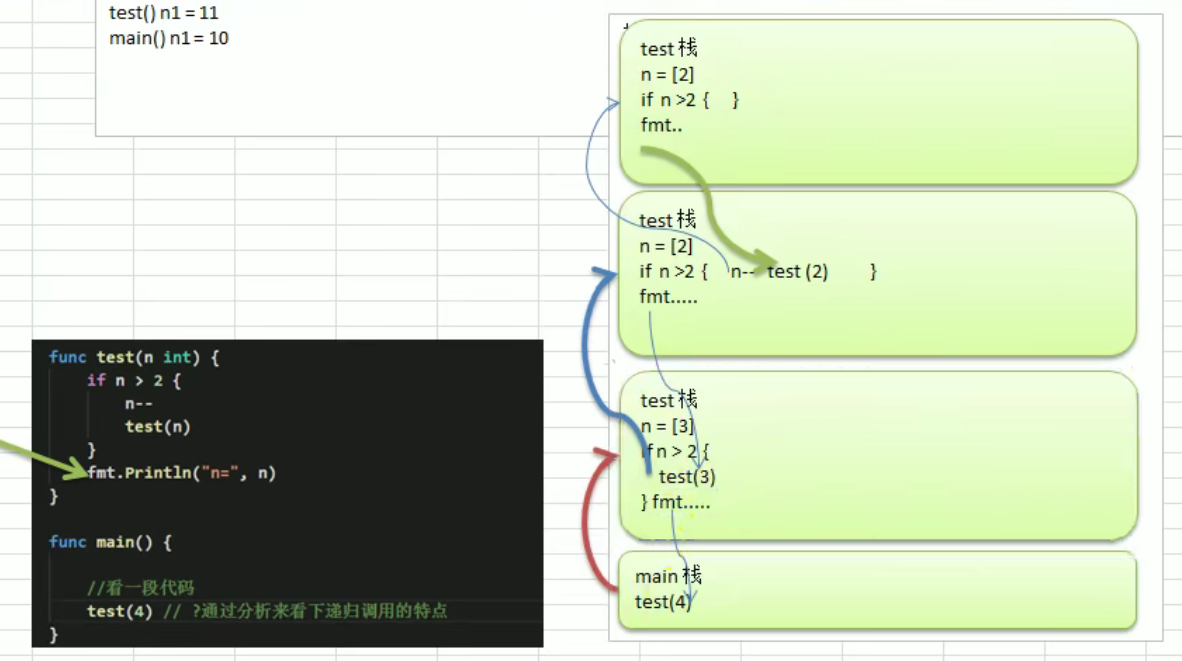
package main
import "fmt"
func test(n1 int) {
    n1++
    fmt.Println("test() n1=", n1)
}
func main() {
    n1 := 10
    test(n1)
    fmt.Println("main() n1=", n1)
}
// test() n1= 11
// main() n1= 10

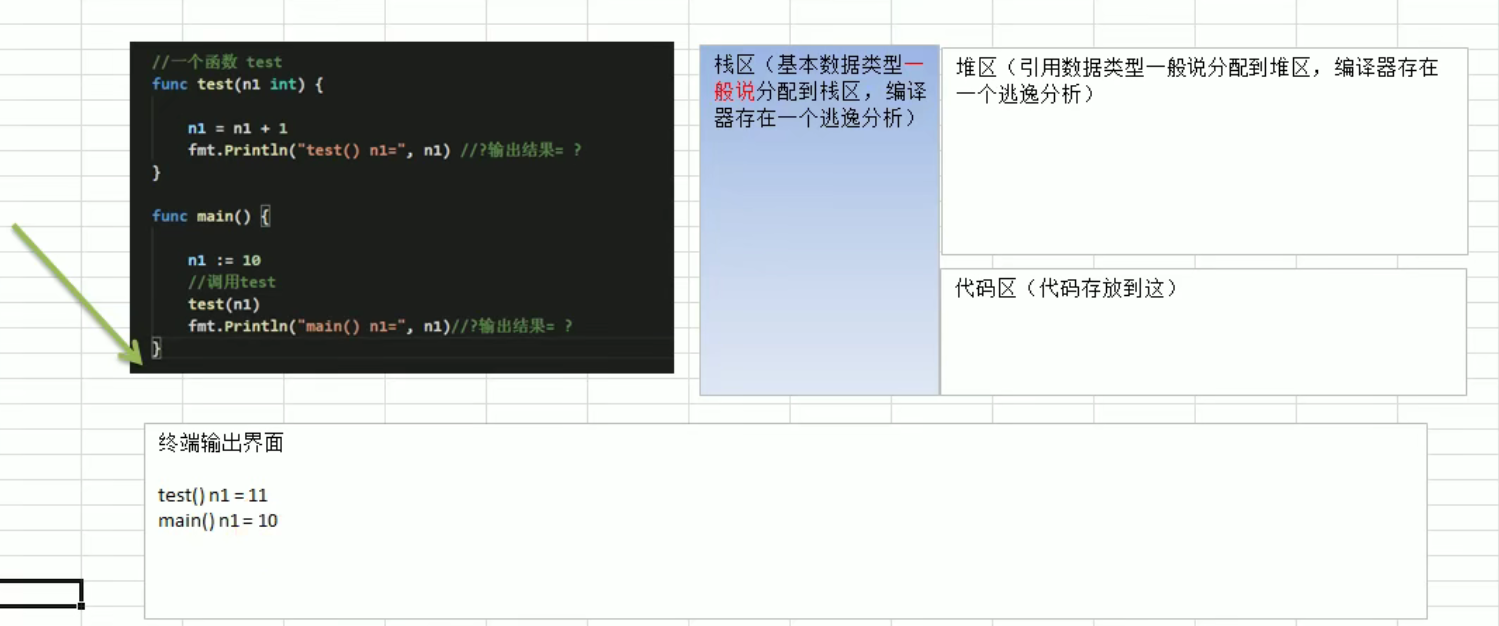
• 在调用函数的时候，会为该函数分配一个新的内存空间（栈），和原有的空间区分开
• 每个函数对应的栈中，数据空间时独立的，不会混淆
• 当一个函数执行完毕后，程序会回收该函数对应的内存空间

return返回值

定义返回值类型列表

func sum(n1 int, n2 int) (int, int) {
    return n1 + n2, n1 - n2 // 返回给调用者
}
func main() {
    total, reduce := sum(10, 20)
    fmt.Printf("total %T %v \n", total, total)
    fmt.Printf("reduce %T %v \n", reduce, reduce)
}
// total int 30
// reduce int -10

函数的递归调用

在函数体内，调用本身
阶层实现

func test(n int) {
    if n > 2 {
        n--
        test(n)
    }
    fmt.Println("n = ", n)
}
func main() {
    test(4)
}
n =  2
n =  2
n =  3

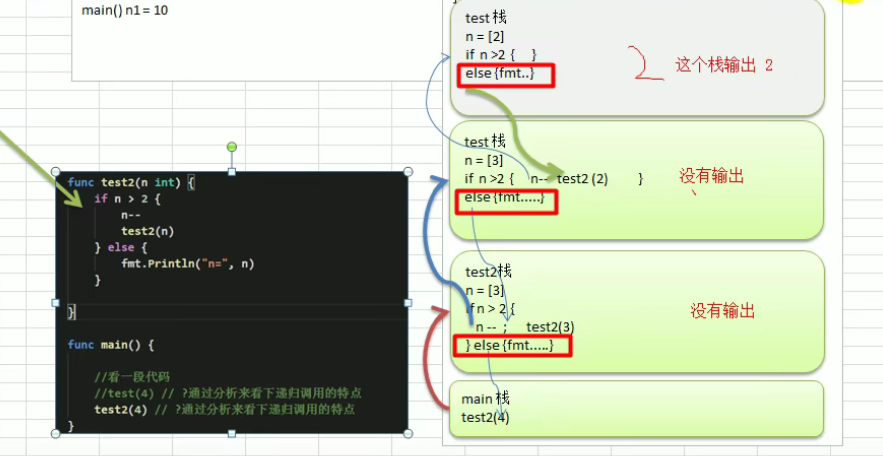
上面递归变形

func test2(n int) {
    if n > 2 {
        n--
        test2(n)
    } else {
        fmt.Println("n = ", n)
    }
}
func main() {
    // test(4)
    test2(4)
}
// n = 2

注意点

1、执行一个函数时，就创建一个新的受保护的独立空间（新函数栈）
2、函数的局部变量是独立的，不会相互影响
3、递归必须向退出递归的条件逼近，否则就无线递归了
4、当一个函数执行完毕，或者遇到return，就会返回，遵守谁调用，就将结果返回给谁。同时该函数被销毁。

斐波那契数

1 ，1 ，2 ，3 ，5 ，8， 13 ，21 ，……
f(n) = f(n-2) + f(n-1)

func fbn(n int) int {
    if n == 1 || n == 2 {
        return 1
    } else {
        return fbn(n-2) + fbn(n-1)
    }
}
func main() {
    // 斐波那契数列
    // 1 ，1 ，2 ，3 ，5 ，8， 13 ，21 ，......
    // f(n) = f(n-2) + f(n-1)
    fmt.Println("value=", fbn(5)) // 第5个斐波那契数
    fmt.Println("value=", fbn(6)) // 第6个斐波那契数
    fmt.Println("value=", fbn(7))
    fmt.Println("value=", fbn(8))
}
value= 5
value= 8
value= 13
value= 21

猴子吃桃问题

// 猴子吃桃子
// 每一天吃当天桃子数量的一半多1个，第十天的时候发现只剩下一个
// 求第一天的桃子数量
func peach(n int) int {
    if n > 10 || n < 1 {
        fmt.Println("您输入的天数不对")
        return 0
    }
    if n == 10 {
        return 1
    } else {
        return (peach(n+1) + 1) * 2
    }
}
fmt.Println("第1天的桃子数量", peach(1))
// 第1天的桃子数量 1534