递归的概念
简单的说:递归就是函数/方法自己调用自己,每次调用时传入不同的变量。递归有助于编程者解决复杂的问题,同时可以让代码变得简洁。
递归的三大要素
- 明确你这个函数想要干什么
- 寻找递归结束条件
- 找出函数的等价关系式
代码
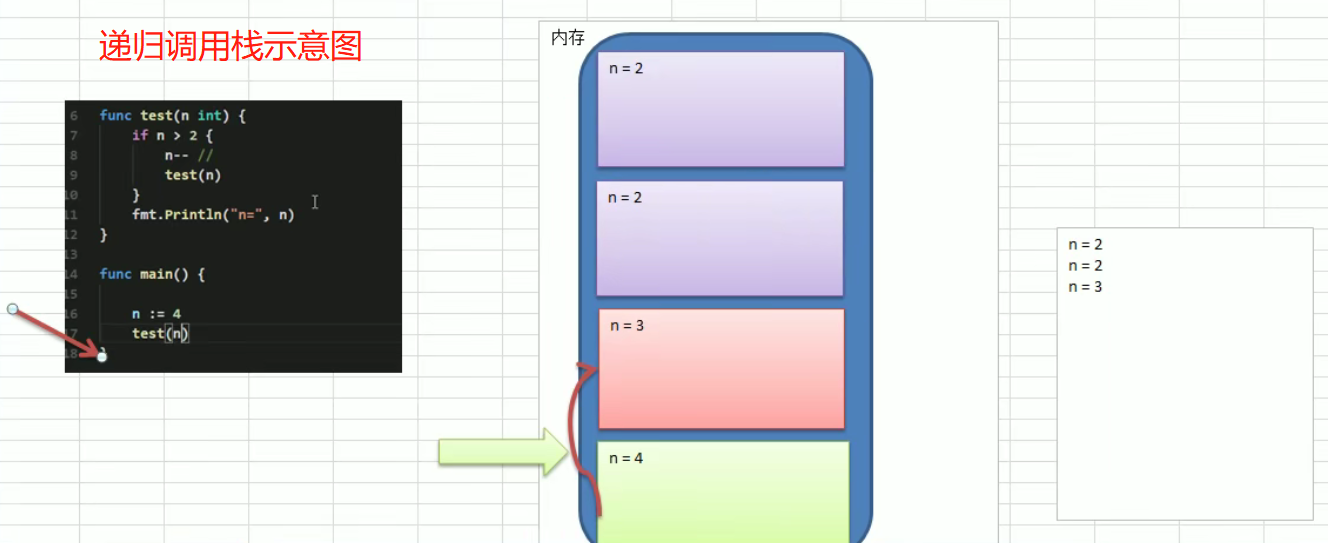
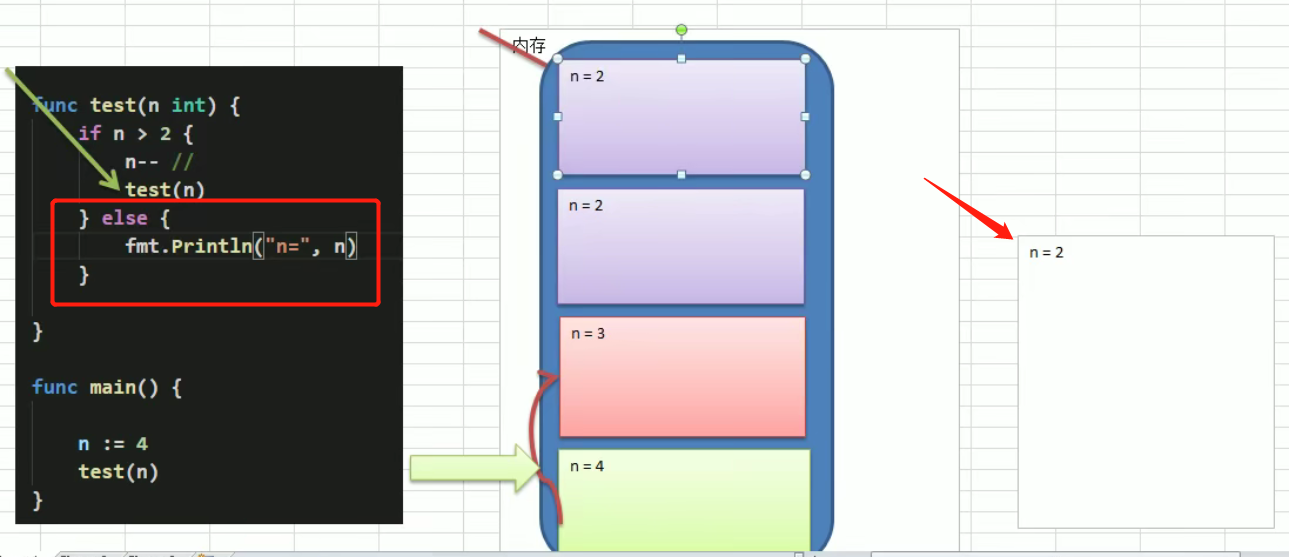
// 递归package mainimport "fmt"func test(n int) {if n > 2 {n--test(n)}fmt.Println("test n = ", n)}func test02(n int) {if n > 2 {n--test02(n)} else {fmt.Println("test02 n = ", n)}}func main() {test(4)test02(4)}/*test n = 2test n = 2test n = 3test02 n = 2*/
递归需要遵守的重要原则
- 执行一个函数时,就创建一个新的受保护的独立空间(新函数栈)
- 函数的局部变量是独立的,不会相互影响。如果希望各个函数栈使用同一个数据,则使用引用传递。
- 递归必须向退出递归的条件逼近,否则就是无限递归,死龟了:)
- 当一个函数执行完毕,或者遇到return,就会返回,遵守谁调用,就将结果返回给谁,同时当函数执行完毕或者返回时,该函数本身也会被系统销毁
应用场景
- 排序
- 二分查找
- 阶乘
- 斐波那契数列
- 猴子吃桃(每一天吃当天桃子数量的一半多1个)
- 8皇后问题
- 汉诺塔(移动圆饼,小的在上,大的在下)
- 迷宫问题
- 球和篮子
- …
// 函数递归调用 + 应用场景package mainimport "fmt"func test(n int) {if n > 2 {n--test(n)}fmt.Println("n = ", n)}func test2(n int) {if n > 2 {n--test2(n)} else {fmt.Println("n = ", n)}}// 斐波那契数func fbn(n int) int {if n == 1 || n == 2 {return 1} else {return fbn(n-2) + fbn(n-1)}}// 猴子吃桃子// 每一天吃当天桃子数量的一半多1个,第十天的时候发现只剩下一个// 求第一天的桃子数量func peach(n int) int {if n > 10 || n < 1 {fmt.Println("您输入的天数不对")return 0}if n == 10 {return 1} else {return (peach(n+1) + 1) * 2}}func main() {test(4)// test2(4)// 斐波那契数列// 1 ,1 ,2 ,3 ,5 ,8, 13 ,21 ,......// f(n) = f(n-2) + f(n-1)fmt.Println("value=", fbn(5)) // 第5个斐波那契数// fmt.Println("value=", fbn(6)) // 第6个斐波那契数// fmt.Println("value=", fbn(7))// fmt.Println("value=", fbn(8))fmt.Println("第1天的桃子数量", peach(1))}