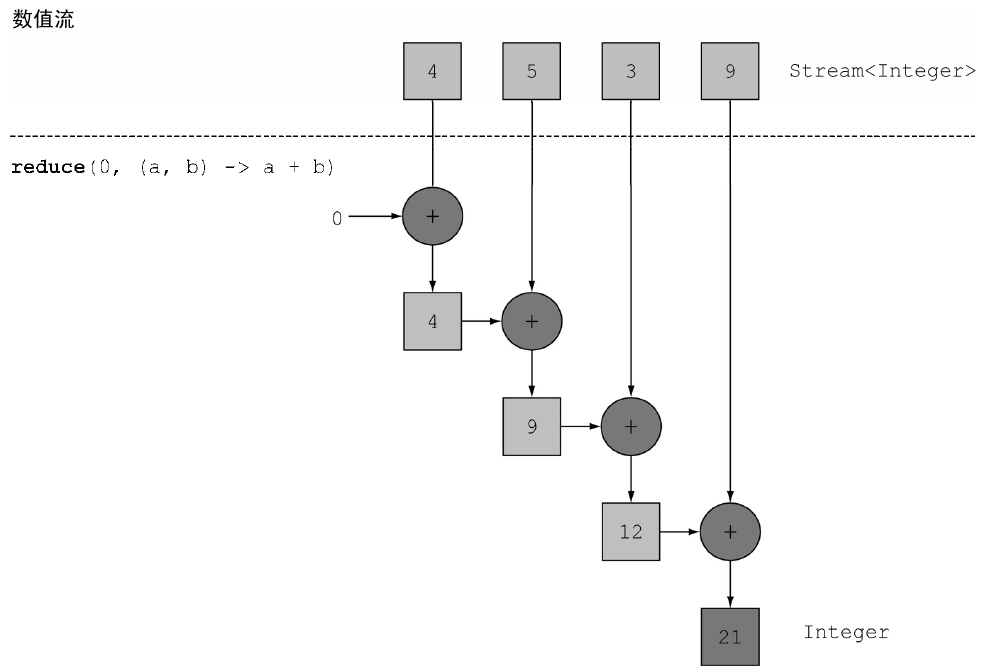
顺序流

  1. public static long sequentialSum(long n) {
  2.         return Stream.iterate(1L, i -> i + 1)
  3.                 .limit(n)
  4.                 .reduce(0L, Long::sum);
  5.     }

1632992585(1).png

将顺序流转换为并行流

  1. public static long parallelSum(long n) {
  2.         return Stream.iterate(1L, i -> i + 1)
  3.                 .limit(n)
  4.                 .parallel()
  5.                 .reduce(0L, Long::sum);
  6.     }

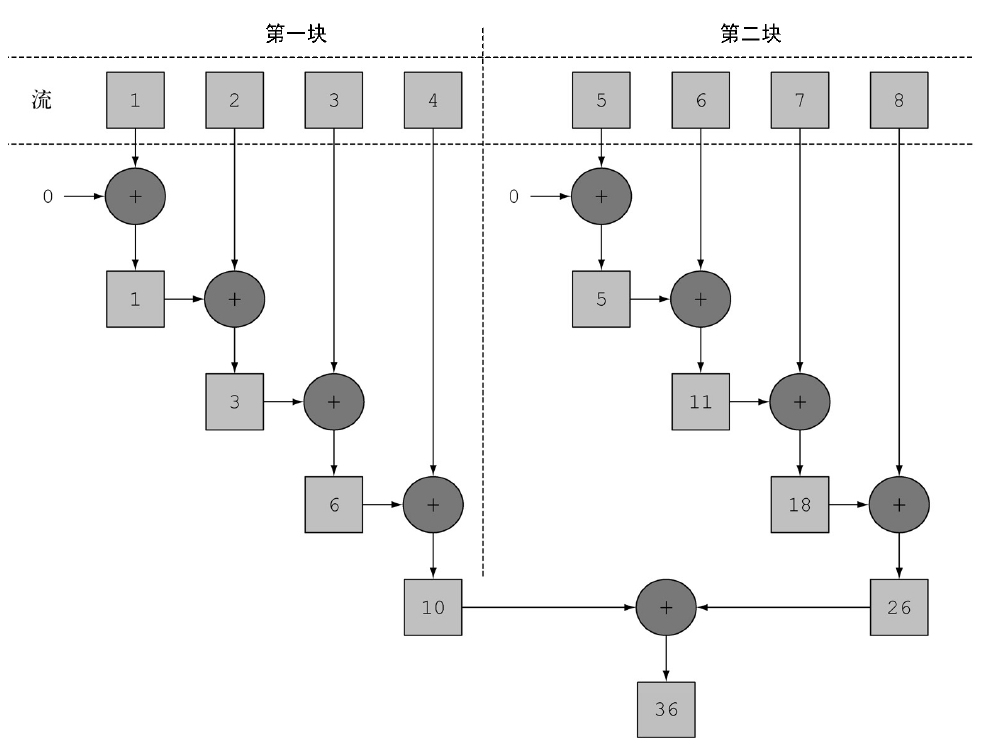
在上面的代码中,对流中所有数字求和的归纳过程的执行方式和上面差不多。不同之处在于Stream在内部分成了几块。因此可以对不同的块独立并行进行归纳操作,如图所示。
最后,同一个归纳操作会将各个子流的部分归纳结果合并起来,得到整个原始流的归纳结果。

1632992665(1).png

测量流性能

  1. public class test {
  2.     public static long sequentialSum(long n) {
  3.         return Stream.iterate(1L, i -> i + 1)
  4.                 .limit(n)
  5.                 .reduce(0L, Long::sum);
  6.     }
  8.     public static long parallelSum(long n) {
  9.         return Stream.iterate(1L, i -> i + 1)
  10.                 .limit(n)
  11.                 .parallel()
  12.                 .reduce(0L, Long::sum);
  13.     }
  15.     public static long iterativeSum(long n) {
  16.         long result = 0;
  17.         for (long i = 1L; i <= n; i++) {
  18.             result += i;
  19.         }
  20.         return result;
  21.     }
  23.     public static long rangedSum(long n) {
  24.         return LongStream.rangeClosed(1, n)
  25.                 .reduce(0L, Long::sum);
  26.     }
  28.     public static long parallelRangedSum(long n) {
  29.         return LongStream.rangeClosed(1, n)
  30.                 .parallel()
  31.                 .reduce(0L, Long::sum);
  32.     }
  34.     public static long measureSumPerf(Function<Long, Long> adder, long n) {
  35.         long fastest = Long.MAX_VALUE;
  36.         for (int i = 0; i < 10; i++) {
  37.             long start = System.nanoTime();
  38.             long sum = adder.apply(n);
  39.             long duration = (System.nanoTime() - start) / 1_000_000;
  40.             if (duration < fastest) fastest = duration;
  41.         }
  42.         return fastest;
  43.     }
  45.     public static void main(String[] args) throws CloneNotSupportedException {
  46.         System.out.println("Sequential sum done in:" +
  47.                 measureSumPerf(test::sequentialSum, 10_000_000) + " msecs");
  48.         // Sequential sum done in:66 msecs
  49.         System.out.println("Iterative sum done in:" +
  50.                 measureSumPerf(test::iterativeSum, 10_000_000) + " msecs");
  51.         // Iterative sum done in:3 msecs
  52.         System.out.println("parallel sum done in:" +
  53.                 measureSumPerf(test::parallelSum, 10_000_000) + " msecs");
  54.         // parallel sum done in:60 msecs
  55.         System.out.println("ranged sum done in:" +
  56.                 measureSumPerf(test::rangedSum, 10_000_000) + " msecs");
  57.         // ranged sum done in:2 msecs
  58.         System.out.println("parallelRanged sum done in:" +
  59.                 measureSumPerf(test::parallelRangedSum, 10_000_000) + " msecs");
  60.         // parallelRanged sum done in:0 msecs
  61.     }
  62. }
  • 顺序流sequentialSum的成绩为66m
  • 用传统for循环的迭代版本执行起来应该会快很多,因为它更为底层，所以iterativeSum的成绩为3m
  • 函数的并行版本的成绩为60m,这相当令人失望,这里实际上有两个问题:

iterate生成的是装箱的对象,必须拆箱成数字才能求和;
我们很难把iterate分成多个独立块来并行执行
第二个问题更有意思一点,因为你必须意识到某些流操作比其他操作更容易并行化。具体来说, iterate很难分割成能够独立执行的小块,因为每次应用这个函数都要依赖前一次应用的结果。
这意味着,在这个特定情况下,归纳进程不是像上图那样进行的;整张数字列表在归纳过程开始时没有准备好,因而无法有效地把流划分为小块来并行处理。把流标记成并行,你其实是给顺序处理增加了开销,它还要把每次求和操作分到一个不同的线程上。

  • 顺序流rangedSum的成绩为2m

LongStream.rangeClosed直接产生原始类型的long数字,没有装箱拆箱的开销。
LongStream.rangeClosed会生成数字范围,很容易拆分为独立的小块。
这个数值流比前面那个用iterate工厂方法生成数字的顺序执行版本要快得多,因为数值流避免了非针对性流那些没必要的自动装箱和拆箱操作。由此可见,选择适当的数据结构往往比并行化算法更重要。

  • 并行流rangedSum的成绩为0m

我们得到了一个比顺序执行更快的并行归纳,因为这一次归纳操作可以像上图那样执行了。这也表明,使用正确的数据结构然后使其并行工作能够保证最佳的性能。

高效使用并行流

留意装箱

自动装箱和拆箱操作会大大降低性能

有些操作本身在并行流上的性能就比顺序流差

limit和findFirst等依赖元素顺序的操作，他们在并行流上执行的代价非常大

对于较小的数据量，选择并行流几乎都不是一个好的决定

并行处理少数几个元素的好处还抵不上并行化造成的额外开销

要考虑流背后的数据结构是否易于分解

例如, ArrayList的拆分效率比 LinkedList高得多,因为前者用不着遍历就可以平均拆分,而后者则必须遍历。另外,用range工厂方法创建的原始类型流也可以快速分解