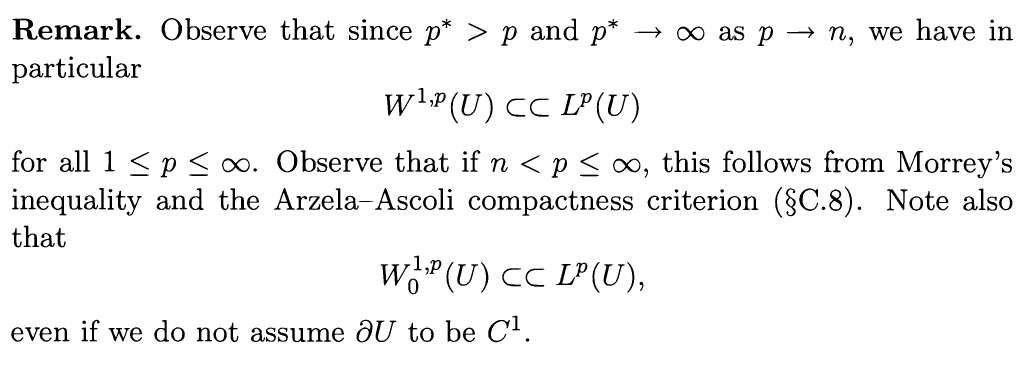迹定理

Lions1972a 中 Chapter 1 定理 9.4 如下

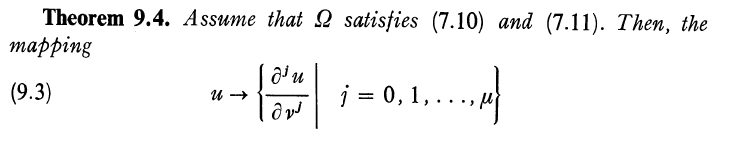
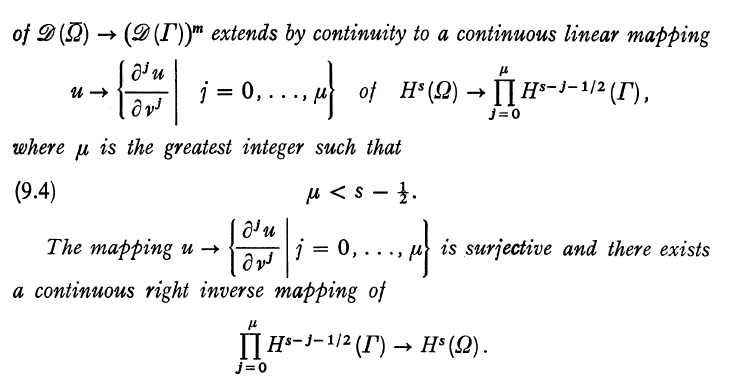
image.png
image.png

其中小于不能改为等于，事实上 Chapter 1 有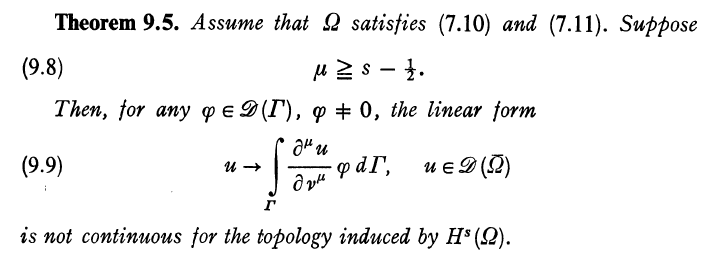
image.png

另外一个常用的迹定理，用来处理边界的，是将 Sobolev 空间相关 - 图4 放松到 Sobolev 空间相关 - 图5 和 Sobolev 空间相关 - 图6 中去，具体参见 Brenner2008 的如下定理：

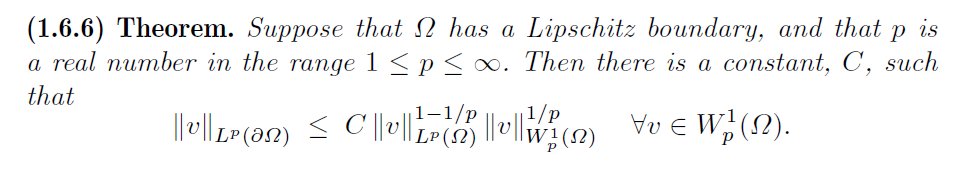
image.png

插值不等式

Lions1972a Chapter 1 中有如下定理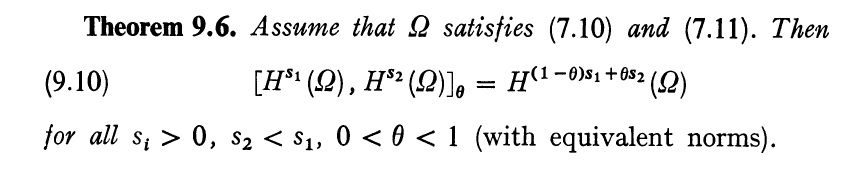
image.png
事实上描述了如下的不等式
Sobolev 空间相关 - 图9

如果涉及到了对时间的积分，即 Hilbert 空间值的插值不等式，参看 Lions1972a Chapter 1 的如下定理

image.png

紧嵌入

对于边界有一定光滑性，则有如下紧嵌入定理
image.png

紧嵌入到 Sobolev 空间相关 - 图12 则更简单

image.png