L07 Normalization

Outline

• Features of Good Relational Design 
• Functional Dependencies 
• Decomposition Using Functional Dependencies 
• Normal Forms 
• Functional Dependency Theory 
• Algorithms for Decomposition using Functional Dependencies 
• Decomposition Using Multivalued Dependencies 
• More Normal Form 
• Atomic Domains and First Normal Form  原子域和第一範式
• Database-Design Process 
• Modeling Temporal Data

Reference

Ch8 关系数据库设计

Functional Dependencies 函數依賴

Ch8 关系数据库设计

数据库系统原理

Use of Functional Dependencies

Seperate them

Decomposition Using Functional Dependencies

Lossless Decomposition

Ch8 关系数据库设计
We can use functional dependencies to show when certain decomposition are lossless.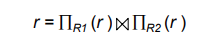

A decomposition of R into R1 and R2 is lossless decomposition if at least one of the following dependencies is in F+ :

Normal Forms

BCNF - Boyce-Codd Normal Form
语雀内容

23 APR

Closure of Functional Dependencies函数依赖理论

记 A->B 表示 A 函数决定 B，也可以说 B 函数依赖于 A。
如果 {A1，A2，… ，An} 是关系的一个或多个属性的集合，该集合函数决定了关系的其它所有属性并且是最小的，那么该集合就称为键码。
对于 A->B，如果能找到 A 的真子集 A’，使得 A’-> B，那么 A->B 就是部分函数依赖，否则就是完全函数依赖。
对于 A->B，B->C，则 A->C 是一个传递函数依赖。

Procedure for Computing F+

To compute the closure of a set of functional dependencies F:

滚雪球算法

F+ = F
repeat
    for each functional dependency f in F+
    apply reflexivity and augmentation rules on f
    add the resulting functional dependencies to F+
  for each pair of functional dependencies f1 and f2 in F+
    if f1 and f2 can be combined using transitivity
      then add the resulting functional dependency to F+ 
until F+ does not change any further

(滚雪球求,F+很少用,计算量巨大)

Closure of Attribute Sets

PDF 22
屬性集閉包
将给定依赖集F下被α函数确定的所有属性的集合称为F下α的闭包 α+

判断α是否为超码
通过检查是否 β ⊆ α+,检查 α -> β 是否成立

Canonical Cover正则覆盖 🌟

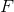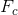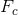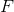的正则覆盖是一个依赖集，使得逻辑蕴含中的所有依赖，并且逻辑蕴含中的所有依赖。此外必须既有如下性质：

• 中任何函数都不含无关属性。
• 中函数依赖的左半部都是唯一的。

Computing a Canonical Cover

R = {A,B,C}        
1. "SPLIT"
2. Remove Extraneous Attributes
3. Remove Redundant FD
F = {
    A > B join C, B > C, A > B, A join B > C 
    A > B, A > C, B > C, A > B, A join B > C  
  A > B, A > C, B > C, A join B > C
  A > B, A > C, B > C, A > C
  A > B (Important) , A > C, B > C
  A > B, B > C
}
(A)+    =        {A, B, C}
(B)+    =        {B, C}

Testing for BCNF (Boyce - Codd Normal Form)

关系模式 R 属于第三范式，且消除了主属性对候选码的部分或传递依赖。

R = (A, B, C, D, E, F)
F = {
    A > BCD,
  D > EF
}
(A, B, C, D, E, F) += {A, B, C, D, E, F}
(A) += { A, B, C, D, E, F} 
(A is Candidate Key)
PRIME ATTRIBUTE = {A}
NOT IN BCNF
- D > EF
(alpha U beta) = {D, E, F}
R - (beta - alpha) 
= {A, B, C, D, E, F} - ( {EF} - {D} )
= { A, B, C, D }

BCNF Decomposition Algorithm

R = A B C D E
F = {
    A -> B,
  BC -> D
}
Superkey -> candidate keys
(ABCDE) += {ABCDE}
(ACE) += {ABCDE}
PRIME ATTRIBUTES = { ACE }
(AC) += {ABCD}
(AE) += {ABE}
(CE) += {CE}
(A) += {AB}
(C) += {C}
(E) += {E}

Canonical Cover

CANONICAL COVER
Fc = {A > B, BC > D}
FC = {A > B, AC > D}
result := {ABCDE}
A > B
result := ((ABCDE) - (AB)) U (AB - B) U (AB))
result := (CDE) U (A) U (AB)
result := (ACDE) U (AB)
AC > D
result := (ACDE)
result := (ACDE) - (ACD) U (ACD - D) U (ACD)
result := (E) U (AC) U (ACD)
result := (ACE) U (ACD) U (AB)
R1(AB): A > B,
R2(ACE),
R3(ACD): AC > D

result = { ABCDE }
BC > D
result := (ABCDE - BCD) U (BCD - D) U (BCD)
result := (AE) U (BC) U (BCD)
result := (ABCE) U (BCD)
A > B
result := ((ABCDE) U (BCD) - (AB)) U (AB - B) U (AB)
result := (BCD) U (CE) U (A) U (AB)
result := (BCD) (ACE) (AB)
BC > D (R1), (R2) (only trivial), A > B (R3)
Dependency - preserving decomposition

Dependency - preserving decomposition

Fc = { A > B, join B > C }
Fc = { A > B, A > C }
R1 = AB, R2 = AC

Primary Key = A,
be sure what is doing

Algorithm of BCNF

Third Normal Form (3NF)

OneTable {
    A -> B -> C
}

If I need to do join updated something if I user 3rd Normal Form
Weaker normal form
No candidate key pointing to someone

Fourth Normal Form

First Normal Form

Ch8 关系数据库设计 - 2. 原子域和第一範式

函数依赖/数据依赖 ——> 设计范式 ——> 避免冗余
Ch8 关系数据库设计

Overall Database Design Process

7.89
Assumed Schema R is given

• Universal relation

ER Model and Normalization

One

Denormalization for Performance

Alternative 1:
Use denormalized relation containing containing attributes of course as well as prereq with all above attributes

Alternative 2:
Materialized view defined a course join prereq

Denormalization Design（反规范化）：
形式上，这个术语指的是对基本表结构的修改，这样新的表比原始的表的规范化程度要低。 但也可以用此属于更宽泛地形容将两个表和并成一个新表的情形，而这个新表与原来的表具有相同的范式，但比原表包含 更多的空值。

对不可改变数据的反模式设计。也就是说对不可改变的数据无需模式化设计。例如，用户信息中要记录该用户的国籍，由于国家信息（国家代码、简称都是不可改变的数据或者说改变的机率很小），所以无需在用户信息表中新增列来关联国家信息表，可以直接将相关的国家信息列作为用户信息表中的列。

Other Design Issues

Modeling Temporal Data

时态数据模型

全时态数据模型
本文采用了基于关系数据模型而设计的双时态数据模型。其与普通的关系数据模型主要的区别在于以下两点，一是数据具有状态属性，二是数据具有时态属性。具有这两种属性的数据模型，称为全时态数据模型。

Reference

Ch8 关系数据库设计

Exam Important

1. Set Closure
2. Canonical Cover
3. Candidate Key
4. Superkey

Final Exam

Final Exam is same as Midterm Exam

• 3 hours
• Do it in ummodle