《数据库系统概论》 （第4版） 个人笔记

6.44 pdf.22

Representing Relationship

create table student (
    ID not null primary key, // Primary Key constraint
)

LN06 第06章 关系数据理论

完整性约束的表现形式

限定属性取值范围：例如学生成绩必须在0-100之间
定义属性值间的相互关连（主要体现于值的相等与否），这就是数据依赖，它是数据库模式设计的关键

数据依赖的类型

函数依赖（Functional Dependency，简记为FD）、
多值依赖（Multivalued Dependency，简记为MVD）、其他

函数依赖：
若对于R(U)的任意一个可能的关系r，r中不可能存在两个元组在X上的属性值相等， 而在Y上的属性值不等， 则称 “X函数确定Y” 或 “Y函数依赖于X”，记作X→Y
（通俗点说，就是X这个属性，决定了唯一一个Y，但反过来不一定）。
所有关系实例均要满足，是一种自然属性。

若 X → Y，Y → X，则记作 X ←→ Y。

如果X→Y，但Y 不是 X的子集，则称X→Y是非平凡的函数依赖（一般情况下讨论的都是这种）
若X→Y，但Y ⊆ X, 则称X→Y是平凡的函数依赖

在R(U)中，如果X→Y，并且对于X的任何一个真子集X’，都有X’ →Y, 则称Y对X完全函数依赖。
若X→Y，但Y不完全函数依赖于X，则称Y对X部分函数依赖。

传递函数依赖

例如：
在关系Std(Sno, Sdept, Mname)中，有： Sno → Sdept，Sdept → Mname
Mname传递函数依赖于Sno

范式的种类：
第一范式(1NF)
第二范式(2NF)
第三范式(3NF)
BC范式(BCNF)
第四范式(4NF)
第五范式(5NF)
各种范式之间存在联系（从小到大的包含关系）：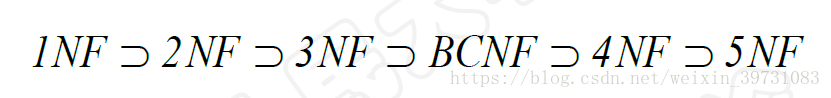

1NF的定义：如果一个关系模式R的所有属性都是不可分的基本数据项，则R∈1NF。
第一范式是对关系模式的最起码的要求。不满足第一范式的数据库模式不能称为关系数据库。
2NF：若R∈1NF，且每一个非主属性完全函数依赖于码，则R∈2NF。
3NF：若R∈3NF，则每一个非主属性既不部分依赖于码也不传递依赖于码。
BCNF：若R∈BCNF：
所有非主属性对每一个码都是完全函数依赖
所有的主属性对每一个不包含它的码，也是完全函数依赖
没有任何属性完全函数依赖于非码的任何一组属性

把低一级的关系模式分解为若干个高一级的关系模式的方法不是唯一的。只有能够保证分解后的关系模式与原关系模式等价，分解方法才有意义。
三种模式分解等价的定义：
⒈ 分解具有无损连接性
⒉ 分解要保持函数依赖
⒊ 分解既要保持函数依赖，又要具有无损连接性

关系数据库理论：范式判断、函数依赖、无损分解、正则覆盖

一、目的、

在查阅数据库设计理论时，发现《数据库系统概论》第5版的概念定义与网上质料有很大不同，不方便大学生做参考质料，并且有一些内容已经没有现实意义了，（如第二范式）。

二、适合阅读人群、

本文内容根据大学教材《数据库系统概论》中文第五版，以自己的理解总结出来的经验，以具体题目来强化概念，在提升做题技巧的基础上增强对概念的理解。适合考试复习参考！

三、内容

约定概念、符号：A属性，α、β属性集，R关系模式。

第一范式：

定义：关系模式R中所有属性都是原子域（atom）

基于函数依赖的范式：

1、约定符号：F函数依赖集，F*函数依赖闭包集

函数依赖定义：如果存在模式（A,B），则A可以做主码，定义为：A → B，例图2

平凡函数依赖（trivial）：

存在α→β，它们在所有的关系中都是满足的（基于现实中的事实判断）。
一般的：β包含于α，则依赖是平凡的（数学抽象判断）。

平凡依赖举例：

R1（学生ID，学生性别，年龄） 学生ID → 学生性别
R2（A,B,C,D,F） F { AB → B } 此处
α = {A，B}，β = {B}

2、BCNF范式定义：

具函数依赖集F的关系模式R属于BCNF范式的条件是：
对于所有 F* 中 α → β 所有函数依赖，以下至少有一个成立：

• ●α→β 是平凡的函数依赖
• ●α 是模式R中的一个超码

3、要求更加宽松的范式，3NF定义：

具有函数依赖集F的关系模式R属于3NF范式的条件是：对于所有F*中所有α→β函数依赖，以下至少有一个成立：
●α→β是平凡的函数依赖
●α是模式R中的一个超码
●α-β中的每一个属性A都包含在R的一个候选码中

4、函数依赖理论

约定符号：F、α属性集闭包

一、函数依赖集闭包（F*）

逻辑蕴涵定义：
给定函数依赖集F，由F出发，可以证明其他的函数也成立，就称这些函数依赖被F逻辑蕴涵。

函数蕴涵举例：
假设关系模式R = {A，B,C,G,H,I} 及 函数依赖集 F {A→B,A→C,CG→H,CG→I,B→H}
则函数依赖： A→H被逻辑蕴涵（可由函数依赖定义推到）
（F*）定义：F逻辑蕴涵的所有函数依赖的集合

armstrong定理（正确有效、完备的）
●自反律 Reflexive Rule：
若α为为一属性集且β⊆α，则有α→β。

●增补律 Augmentation Rule：
若有α→β且λ为一属性集，则有λα→λβ。

●传递律 Transitivity Rule：
若有α→β及β→λ，则有α→λ。

派生的规则（简化计算），可由Armstrong推导出
●合并律 Union Rule：
若有α→β及α→λ，这则有α→βλ。

●分解律 Decomposition Rule：
若有α→βλ，则有α→β及α→λ。

●伪传递律 Pseudotransitivity Rule：
若有 α→β 及 λβ → σ ，则有 αλ → σ。

函数依赖集闭包举例：
假设关系模式R={A，B,C,G,H,I}及函数依赖集
F{ A→B, A→C, CG→H, CG→I, B→H}
推导：
A → H，传递律；
CG → HI，合并律；
AG→H，伪传递律 { A -> C, CG -> H => AG -> H }；

上面求出的函数依赖并不完整，求F的闭包F*的算法可查阅《数据库系统理论》

二、属性集闭包：

如果有 α→B，我们就称B被函数α函数确定。判断一个集合α是否为超码，可设计一个有α函数确定的属性集（α*）算法,如果确定的属性集包含了R关系模式所有属性，则集合α是超码。
属性集闭包的作用：

属性集闭包定义：
令α为一属性集，我们称函数依赖集F下有α函数确定的所有属性的集合为F下α的闭包，记为α*。

算法：

result：=α
while（result发生变化）
  for each 函数依赖β→λ inF do
  begin
  if β⊆result then result:=result∩λ ；
end

属性依赖集闭包举例：
　例如，已知关系模式R(U,F)，U={A,B,C,D,E,G}，F={AB→C,D→EG,C→A,BE→C,BC→D,AC→B,CE→AG},求(BD)+
　解：
　① (BD)+ = {BD}；
　② 计算(BD)+ ，在F中扫描函数依赖，其左边为B,D或BD的函数依赖，得到一个D→EG。所以，(BD)+= {BDEG}。
　③ 计算(BD)+，在F中查找左部为BDEG的所有函数依赖，有两个：D→EG和BE→C。所以(BD)+＝{(BD)∪EGC}={BCDEG}。
　④ 计算(BD)+，在F中查找左部为BCDEG子集的函数依赖，除去已经找过的以外，还有三个新的函数依赖：C→A,BC→D,CE→AG。得到(BD)+＝{(BD)∪ADG}＝{ABCDEG}。
　⑤ 判断(BD)+=U，算法结束。得到(BD)+＝{ABCDEG}。
说明：上面说明(B,D)是该关系模式的一个超码。

属性集闭包的作用：
1：判断α是否为超码，通过计算α，看α是否包含了R中所有属性。
2：通过验证是否β⊆α*，验证函数依赖α→β是否成立（证明正则覆盖）

三、正则覆盖（canonical cover）：

无关项（extraneous attribute）定义：若果去除函数依赖中的属性不会改变函数依赖的闭包，就称该属性是无关的。
形式定义：
●如果A∈α并且F逻辑蕴涵（F-{α→β}）U{(A-α)→β},则A在α是无关的
●如果A∈β并且函数依赖{F-{α→β}）U{α→（β-A）}逻辑蕴涵F，则A在β是无关的（下面有例题）

检验方法：
令R为一关系模式，F是在R上成立的给定的函数依赖集。考虑依赖α→β上的属性A。
●如果A∈α，令λ=α-{A}，并且计算λ→β是否可以由F推出。
●如果A∈β，F’=（F-{α→β}）U{α→（β-A）}，并检验α→A是否能够由F’推出。

&正则覆盖定义：F的正则覆盖Fc是一个依赖集，使得F与Fc相互逻辑蕴涵。此外，还包含如下性质：
●Fc中任何函数依赖都不含无关属性。
●Fc中函数依赖左半部分都是唯一的。即，Fc中不存在α1→β1，α2→β2，满足α1=α2。

正则覆盖举例：
可证明Fc与F具有相同的闭包，验证是否满足Fc等价于验证是否满足F。
设：R(A,B,C)及F{A→BC，B→C,A→B,AB→C}
求Fc？

解法一：运用算法和定义
令Fc=F={A→BC，B→C,A→B,AB→C}
①合并A→BC，A→B 为：A→BC
得：Fc={A→BC，B→C,AB→C}
②A在AB→C中是无关的，因为Fc逻辑蕴涵（Fc-{α→β}）U{(A-α)→β}={B→C,AB→C}
得Fc={A→BC,B→C}
③ C在A→BC中是无关的，（Fc-{α→β}）U{α→（β-A）}={A→B，B→C}逻辑蕴涵Fc。
得：Fc={A→B,B→C}

解法二：可利用上面检验方法检验。（略）

四 无损连接：

设关系模式R与函数依赖集F，R分解为R1，R2，此分解是无损的必须满足：α=R1∩R2是R1或R2的超码，可利用属性集闭包验证。

五 保持依赖：

保持依赖的判断：
如果F上的每一个函数依赖都在其分解后的某一个关系上成立，则这个分解是保持依赖的（这是一个充分条件）。
如果上述判断失败，并不能断言分解不是保持依赖的，还要使用下面的通用方法来做进一步判断。
该方法的表述如下：

算法二：
对F上的每一个α→β使用下面的过程：

result:=α;
  while(result发生变化)do
    for each 分解后的Ri
      t=(result∩Ri)+ ∩Ri
      result=result∪t

这里的属性闭包是在函数依赖集F下计算出来的。如果result中包含了β的所有属性，则函数依赖α→β。分解是保持依赖的当且仅当上述过程中F的所有依赖都被保持。

无损连接与保持依赖举例：
●设关系模式R(U,F)，其中U=｛A, B, C, D, E｝，F＝{A→BC，C→D，BC→E，E→A｝，则分解ρ={R1（ABCE），R2（CD）｝满足 （43） 。
（43） A．具有无损连接性、保持函数依赖
B．不具有无损连接性、保持函数依赖
C．具有无损连接性、不保持函数依赖
D．不具有无损连接性、不保持函数依赖

先做无损链接的判断。R1∩R2={C}，计算C+。
Result=C
由于C→D，C∈result，所以result=result∪D=CD
可见C是R2的超码，该分解是一个无损分解。
再做保持依赖的判断。
A→BC，BC→E， E→A都在R1上成立（也就是说每一个函数依赖左右两边的属性都在R1中），C→D在R2上成立，因此给分解是保持依赖的。

选A。

再看一个复杂点的例题。

●给定关系模式R(U,F)，U=｛A, B, C, D, E｝，F＝{B→A，D→A，A→E，AC→B｝，其候选关键字为
（40） ，则分解ρ={R1（ABCE），R2（CD）｝满足 （41） 。（40）
A．ABD
B．ABE
C．ACD
D．CD

A．具有无损连接性、保持函数依赖
B．不具有无损连接性、保持函数依赖
C．具有无损连接性、不保持函数依赖
D．不具有无损连接性、不保持函数依赖

看见了吧，和前面一题多么的相像！
对于第一问，分别计算ABCD四个选项的闭包，
（ABD）+ = { ABDE }
（ABE）+ = { ABE }
（ACD）+ = { ABCDE }
（CD）+ = { ABCDE }
选D。

再看第二问。
先做无损链接的判断。R1∩R2={C}，计算C+。
result=C

因此C既不是R1也不是R2的超码，该分解不具有无损分解性。
再做保持依赖的判断。

B→A，A→E，AC→B在R1上成立，D→A在R1和R2上都不成立，因此需做进一步判断。
由于B→A，A→E，AC→B都是被保持的（因为它们的元素都在R1中），因此我们要判断的是D→A是不是也被保持。

对于D→A应用算法二：
result=D
对R1，result∩R1=ф（空集，找不到空集的符号，就用这个表示吧），t=ф，result=D
再对R2，result∩R2=D，D+ =ADE ，t=D+ ∩R2=D，result=D
一个循环后result未发生变化，因此最后result=D，并未包含A，所以D→A未被保持，该分解不是保持依赖的。

选D。

四、BCNF与3NF比较：

基于多值依赖的范式
4ＮＦ定义：

4NF是比BCNF更加严格的范式，属于BCNF的范式一定属于4NF范式，但属于4NF不一定属于BCNF

范式判断
方法：
充分运用属性集闭包判断是否属于BCNF，
再判断是否属于3NF，此处主要要求是候选码，把判断出来的超码进行拆分，在求独自的属性闭包集，判断是否是超码。是，则不是候选码，反之亦然。
（候选码：最小的超码）。

五、关系型数据库设计总结：