- Normalization of Database—— 数据库的正规化
- Normalization of Database
- Problems Without Normalization
- 正规化的规则
- First Normal Form (1NF)
- Second Normal Form (2NF)
- Third Normal Form (3NF)
- 怎么消除传递依赖?
- Boyce and Codd Normal Form (BCNF)
- Fourth Normal Form (4NF)
Normalization of Database—— 数据库的正规化
Recall:
数据库中的一些术语:(后面的中文可能翻译不准确,我自己这么称呼它们)
relation —— 关系模型
tuple entity —— 表中的一条记录,也成为实体
attribute/column —— 每个表头即属性
domain —— 属性的取值域
FD(functional dependency)—— 函数依赖
MVD(Multi-Valued Dependency) —— 多值依赖。。这个真不知道该怎么翻译
Relation
| Attribute / Column | ||
|---|---|---|
| 1 | (Domain) | |
| Tuple Entity 2 | 2 |
Normalization of Database
数据库正规化是数据库中如何合理且有效组织数据的一门技术,它也为我们提供了一套系统地消除数据冗余(redundancy)和异常(anomaly)的方法。
正规化主要就是两个目的:
- 消除数据冗余(或者说没意义的数据)
- 确保数据之间的依赖关系是合乎逻辑的
Problems Without Normalization
假如在设计数据库关系的时候没考虑正规化,不仅会因为数据间的冗余从而浪费存储空间,同时,它也会给我们更新、删除数据时带来很多麻烦,也就是上面说到的异常,下面举例说明。
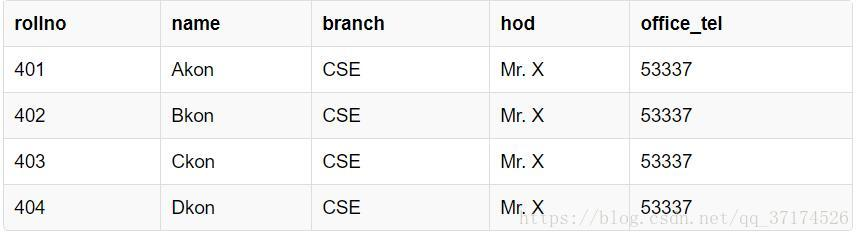
表头分别是学生id,学生姓名,学生具体的专业方向,hod (Head of Department) 学院的领导,办公电话。
01 插入异常
假如来了个新生,他还没细分具体专业方向,于是乎在后三栏我们就没办法添了,只能用NULL来补充了,这样就很不方便了;
相反,假如软件工程专业有50个学生,那么这50个学生的后三栏就会重复,但我们不得不重复地插入。
02 更新异常
好,假如某天Mr. X不当领导了,然后换了个领导Mr. Y,那么每个学生都需要将他的hod改成Mr. Y了。万一数据库管理员不小心漏了几个同学的没改,那这些学生的学籍就有错误了。
也许你会说:哎呀,那你管理员细心一点不就好了?
那我会说:你为什么不可以换一种设计数据表的方式呢?
03 删除异常
再假设,某个branch只有一个学生(好像不太可能),有一天,这个学生真的太孤单了,他读不下去了,转去学管理了,很显然就要把他的信息删掉,问题就来了。因为我们的学生信息和专业的信息是绑在一起的,你删了这个唯一的同学,那这个专业、专业领导也被你删掉了,这样就有问题了。
正规化的规则
主要分为以下几种(越往后,要求越严格):
- First Normal Form
- Second Normal Form
- Third Normal Form
- BCNF(Boyce-Codd Normal Form)
- Fourth Normal Form
First Normal Form (1NF)
如果一个表是满足一范式的,那么它需要满足以下条件:
- 每个属性的取值必须是原子的atomic
每列的取值必须是单个值(single value),稍后举例说明 - 每一列的domain必须是一样的
很显然,取值要不然是字符串,要不然是int,总之每列的数据类型不能不一样. - 不存在相同的列名
列名一定不能相同,不然BDMS会产生混淆 - 列的排列顺序,以及每个tuple间的排列顺序可以交换。
第一列可以放在第二列,第一行也可以放到第二行去,这都不影响。
Example
| roll_no | name | subject |
|---|---|---|
| 101 | Akon | OS, CN |
| 103 | Ckon | Java |
| 102 | Bkon | C, C++ |
当前已经满足了4个条件中的3个,唯独第一条原子性不满足,subject对应的取值可能有多个,即它是multi-value的,而不是 atomic 的。
解决办法
非常简单,把multi-value给它一个一个拆成single value,如下所示:
| roll_no | name | subject |
|---|---|---|
| 101 | Akon | OS |
| 101 | Akon | CN |
| 103 | Ckon | Java |
| 102 | Bkon | C |
| 102 | Bkon | C++ |
其实第一范式是非常非常基础的要求了,几乎没做什么强的限定。4条约束也是十分自然
Second Normal Form (2NF)
如果一个表是满足二范式的,那么它需要满足以下条件:
- 它必须是满足一范式的
- 它不含有部分依赖(Partial Dependency)
那什么又是 partial dependency 呢?别急,我们慢慢道来。
什么是 Functional dependency (函數依赖)?
假设我们有一张Student表,该表包含以下字段student_id, name, reg_no(注册号), branch(专业) 和address(家庭住址)。我们都知道,student_id可以唯一地决定一条学生记录,那么student_id可以做主键。
Student
| student_id (Primary) |
name | reg_no | branch | address |
|---|---|---|---|---|
| 10 | Akon | 07-WY | CSE | Kerala |
| 10 | Akon | 08-WY | IT | Gujarat |
那么,如果我已经知道了student_id,那我也就知道了他的branch、name等等信息,换句说就是student_id 决定了branch,也决定了 name,像这种谁某一列(或多列)决定了其它列(或多列),
我们就成之为依赖,也有的地方称为 functional dependency (函数依赖)。

什么是 partial dependency (部分依赖)?
假设我们现在有个表Subject,包含subject_id,subject_name
Subject
| subject_id (Primary) |
subject_name |
|---|---|
| 1 | Java |
| 2 | C++ |
| 3 | Python |
又有一张新的Score表,包含score_id, student_id, subject_id, marks, teacher字段
Score
| score_id | student_id (Primary) |
subject_id (Primary) |
marks | teacher |
|---|---|---|---|---|
| 1 | 10 | 1 | 70 | Java Teacher |
| 2 | 10 | 2 | 75 | C++ Teacher |
| 3 | 11 | 1 | 80 | Java Teacher |
对于 Score 表来说,student_id + subject_id 是该表的 candidate Key(候选码),
我们就选这个候选码作为主码。
好的,那么看一下teacher这个字段,它的依赖关系应该是,一个课程决定了该课程的老师是谁,也就是说,
存在 subject_id —> teacher 的 functional dependency,但是这个函数依赖的决定因素subject_id只是主键的一部分,并且和主键中的student_id没什么关系,像这样的,我们依赖称之为 partial dependency 部分依赖。
怎么消除部分依赖?
很简单,只要把存在部分依赖的那一列元素单独拉出来就OK。
在上面的Score表中,我们把teacher列拉出来,刚好它是依赖于subject_id的嘛,所以,就把teacher列拉到Score表中去。操作之后就像下面这样:
Subject
| subject_id | subject_name | teacher |
|---|---|---|
| 1 | Java | Java Teacher |
| 2 | C++ | C++ Teacher |
| 3 | Php | Php Teacher |
Score
| score_id | student_id | subject_id | marks |
|---|---|---|---|
| 1 | 10 | 1 | 70 |
| 2 | 10 | 2 | 75 |
| 3 | 11 | 1 | 80 |
Third Normal Form (3NF)
如果一个表是满足三范式的,那么它需要满足以下条件:
- 它必须是满足二范式的
- 它不含有传递依赖(Transitive Dependency)
A > B, B > C => A > C
Student Table
| student_id (Primary) |
name | reg_no | branch | address |
|---|---|---|---|---|
| 10 | Akon | 07-WY | CSE | Kerala |
| 11 | Akon | 08-WY | IT | Gujarat |
| 12 | Bkon | 09-WY | IT | Rajasthan |
Subject Table
| subject_id (Primary) |
subject_name | teacher |
|---|---|---|
| 1 | Java | Java Teacher |
| 2 | C++ | C++ Teacher |
| 3 | Php | Php Teacher |
Score Table
| score_id (Primary) |
student_id |
subject_id | marks |
|---|---|---|---|
| 1 | 10 | 1 | 70 |
| 2 | 10 | 2 | 75 |
| 3 | 11 | 1 | 80 |
现在我想在Score表里面多加一点信息,说明一下,原来 Score 表中的 marks 我们看作是平时成绩,现在附加上exam_name和total_marks两个字段。
Score_Insert
| score_id |
student_id (Primary) |
subject_id (Primary) |
marks | exam_name | total_marks |
|---|---|---|---|---|---|
修改后,exam_name 字段还是依赖于主键(student_id,subject_id)的,
毕竟不同专业的学生会有不一样的考试,相同专业的不同考生也有不一样的考试嘛。
可是total_mark就不太一样了。因为不同考试的算分策略不一样,有的是平时成绩和考试成绩三七开,有的四六开,所以total_marks是取决于exam_name的,
exam_name > total_marks
但是这张表的主键又是(student_id,subject_id),
这样transitive dependency(传递依赖)的定义也就来了:
Transitive Dependency: When a non-key attribute depends on other non-key attributes rather than depending upon the key attributes or primary key.
也就是说,一个非码的属性依赖于另一个(或几个)非码属性,这样的依赖就成为传递依赖。
也就如Score表中的total_marks是取决于exam_name的,
而主码是(student_id,subject_id)
怎么消除传递依赖?
把传递依赖的那几列单独放到另一张表去,再设置一个新的列来代替Score表中关于考试的信息。
The new Score Table
| score_id | student_id (Primary) |
subject_id (Primary) |
marks | exam_id |
|---|---|---|---|---|
The new Exam table
| exam_id (Primary) |
exam_name | total_marks |
|---|---|---|
| 1 | Workshop | 200 |
| 2 | Mains | 70 |
| 3 | Practicals | 30 |
Boyce and Codd Normal Form (BCNF)
Boyce-Codd Normal Form 是 Third Normal Form 的一种扩展,因此有时候也被称为3.5范式。
BCNF其实是第三范式的更高约束版本,它可以处理一些3NF处理不了的异常
如果一个表是满足BCNF的,那么它需要满足以下条件:
- 它必须是满足三范式的
- 对任意一个FD ( X → Y ), X 应该是个超键(superkey).
在讲BCNF之前,我们需要知道许多其他的一些概念,下面一一叙述,别怕,很简单的。
Functional dependency(函数依赖)
它的定义如下:
if two tuples of R agree on all of the attributes A1 A2 A3…An (i.e., the tuples have the same values in their respective componets for each of these attributes), then they must also agree on all of another list of attributes B1B2B3…Bn. So, we write this FD formally as:
A1 A2 A3 … An → B1 B2 B3 … Bn −−−−−−−−−−−−−− ①
也就是说,假如对任意两个元组在 A1 A2 A3 … An属性的取值相同,那么他们俩在B1 B2 B3 … Bn 属性的取值也肯定相同,那么我们就称 ① 式子为一个FD。
举个很简答的例子,为了减少数据的冗余,我们希望在一个叫StuInfo的表中,只有学生的id和name字段,那么对任何两个记录,只要id是相同的,那么姓名也必定相同,那么这个 id → name 就是一个FD(函数依赖).
StuInfo Table
| ID | name | hobby |
|---|---|---|
FD 的性质
假设X,Y,Z都是relation R上的一些属性。
01 Reflexivity(自反性):
如果 Y 是X的子集, 那么 X → Y. 例如:X= {ID, NAME}and Y={ID},显然, X → Y是正确的。
02 Augmentation(这个我真不知道怎么翻译):
If X → Y, then X Z → Y Z.
也就是说在FD的左右两边同时加上相同的属性,新的FD也是成立的。
03 Transitivity(传递性):
If X → Y and Y → Z, then X → Z.
03 Splitting / Combining Rule(分解/合并规则):
如果 A1A2A3…An → B1 B2 B3 … Bn,那么A1A2A3…An →B1,A1A2A3…An →B2,… A1A2A3…An →Bn都是对的,这就是split啦,反过来就是combine了。
04 Attribute Closure(属性的闭包):
所有由 A 决定的属性的集合叫做A的闭包,记为 A+.
另:如果 Y 是X的子集, 那么X → Y我们称为 trivial FD(平凡FD);
反之,如果 Y 不是 X 的子集,那么我们称之为 non-trivial FD(非平凡FD)
Keys of Relations(关系的keys)
定义如下:
如果一个属性的集合{A1A2A3…An}是一个relation的key,那么这些属性也决定了整个relation上的所有 attributes的取值。
这样可能显得有点抽象,继续采用上面StuInfo的例子,如果只有学生的id和name字段,且存在id → name 的 FD,那么显然id这个属性(也可以说是只有一个元素的集合)就决定了StuInfo这个 relation的所有属性的取值;
| ID | name | hobby |
|---|---|---|
如果还有一个hobby的字段,那么{id}就不是这个relation的key了,对,{id,hobby}就可以是key了。既然{id,hobby}是key,那{id,name,hobby}也肯定是一个字段了,
于是又引申出minimal key和superkey的概念了。
Minimal key
当一个key的属性不能再减少时,它就是一个minimal key了。
Superkey
包含minimal key的任何属性集合都叫做superkey。
是的,我们上面的例子中,{id,hobby},{id,name,hobby}都是key,并且{id,name}是minimal key,{id,name,hobby}是 superkey。
3. Closure of Attributes(属性的闭包)
在讲到FD的性质的时候,我们提到了属性的闭包这个概念,下面我换个方法,先举例子,再写定义。
继续StuInfo这个relation,现在有id,name,birthday,university,u_city,u_country这些属性,
| ID | name | hobby | birthday | u_city | u_country |
|---|---|---|---|---|---|
还有以下FDs:
id > name,birthday,university > u_city,u_city > u_country
ok,那么id的闭包就是{id,name}了,university 的闭包 closure of attributes 就是{u_city,u_country}了,看一眼你大概知道是怎么操作得来的吧?
算法:
计算属性集合的闭包
输入:
待求属性集合A={ A1 A2 A3 ... An},所有给定的FD集合S
输出:
A的闭包
如果必要,对S中的每个FD,将它的右边全部根据split规则分解成右边只有一个属性的FD。
2. 初始化X=A,X最终会是我们要求的闭包
3. 重复以下过程:
对所有 B1B2B3…Bn→C的FD,
其中B1B2B3…Bn都在X中,但是C不在X中,直到再也找不到这样的C。
由于属性个数是有限的,所有以上步骤肯定是可以在有限步骤内完成的。返回X,它就是A的闭包。
属性依赖集闭包举例:
例如,
已知关系模式 R(U,F),U={A,B,C,D,E,G},F={ AB → C, D → EG, C → A, BE → C, BC → D, AC → B, CE → AG},
求 (BD)+
解:
① (BD)+ = {BD};
② 计算(BD)+ ,
在F中扫描函数依赖,其左边为B,D或BD的函数依赖,得到一个 D → EG。
所以,(BD)+= { BDEG }。
③ 计算(BD)+,
在F中查找左部为BDEG的所有函数依赖,有两个:D → EG 和 BE → C。
所以(BD)+= {(BD) ∪ EGC} = { BCDEG }。
④ 计算 (BD)+,
在F中查找左部为BCDEG子集的函数依赖,除去已经找过的以外,
还有三个新的函数依赖:C → A , BC → D, CE → AG。
得到 (BD)+= { (BD) ∪ A D G } = {ABCDEG}。
⑤ 判断(BD) += U,算法结束。
得到(BD) += {ABCDEG}。
说明:上面说明(B,D)是该关系模式的一个超码。
属性集闭包的作用:
1:判断α是否为超码,通过计算α,看α是否包含了R中所有属性。
2:通过验证是否β⊆α*,验证函数依赖α→β是否成立(证明正则覆盖)
Rules for BCNF
一个relation满足BCNF,它必须满足以下条件:
- 它必须满足 Third Normal Form.
- 对任意 non-trivial(非平凡的) FD A → B, A 必须是个superkey。
Example
假设一个schema如下:{title,year,studioName,president,presAddr}
有以下FD:
title , year > studioName ②studioNamer > president ③president > presAddr ④
从以上我们可以得知,只有{title,year}是这个relation的key,可以简单推导验证。
那么 ② 是满足BCNF的(它的左边就是一个key),可是③④就都违反了BCNF的第二个条件了,所以上面这个relation就说明设计存在问题,会导致数据冗余。怎么办?
别急,有一个叫做BCNF Decomposition的算法,
它可以帮助我们将不满足规则的relation分解成两个或多个relations,使得它们各自满足BCNF。
BCNF Decomposition algorithm
输入:给定原始relation R0,所有给定的 FD 原始集合S0.
输出:两个或多个 relations,使得它们各自满足BCNF
检查R0是否满足BCNF条件,如果满足,直接返回R0。
找到任意一条违反BCNF的FD,
X → Y,使用属性集合的闭包算法,计算X的闭包X+。
令R1 = X+,R2包含两部分,一部分是X,另一部分是在R中但不在X+中的属性。根据 R1 和 R2 对原始FD集合S0运用projection算法进行“分割”,对应记作S1和S2。
递归地对R1和R2调用本算法,直到所有relations都满足BCNF。
关于步骤3中说的的 projection 算法 ,我就不再叙述了,给个> 链接 <,很简单的。
以上就是关于BCNF的主要内容了,当然BCNF也有一个shortcoming,以后会陆续更新,如果理解不当,还请留言指出!
Example of BCNF Decomposition algorithm
Reference
【1】 A First Course in Database System , UJeffrey D.llman, Jennifer Widom,Stanford University
Andy
2018-9-25 23:02
Canonical Cover
Computing a Canonical Cover
Fourth Normal Form (4NF)
如果一个表是满足三范式的,那么它需要满足以下条件:
- 它必须是满足BCNF的
- 它不含有多值依赖( Multi-Valued Dependency.)

————————————————
版权声明:本文为CSDN博主「Liu Zhian」的原创文章,遵循CC 4.0 BY-SA版权协议,转载请附上原文出处链接及本声明。
原文链接:https://blog.csdn.net/qq_37174526/article/details/82776291

