机器学习

实现人工智能的手段，主要研究内容为如何利用数据或经验进行学习，改善具体算法的性能
概率论、统计学、算法复杂理论
网络搜索、邮件过滤、推荐系统、广告投放、信用评价、欺诈检测、股票交易、医疗诊断
监督学习（supervised learning） 人类标注结果
无监督学习（unsupervised learning）
强化学习（reinforcement learning,增强学习）根据环境学习来做出判断
半监督学习（semi-supervised learning）
深度学习（deep learning） 深层神经网络模型

无监督学习

利用无标签的数据 学习数据的分布、数据与数据之间的关系
标签
聚类和降维
聚类：根据数据的“相似性”将数据分为多类的过程
评估两个不同样本之间的相似性，通常使用方法计算两个样本之间的距离。使用不同的方法计算样本之间的距离会关系到聚类结果的好坏。
欧式距离、曼哈顿距离（十字路口距离）、马氏距离（协方差距离）夹角余弦（两个向量的相似，用他们夹角的余弦衡量，1为最相似）
降维：保证数据所具有的代表性特性或者分布的情况下，将高维转向地位
可视化、精简数据

scikit-learn

工具集 开源 可覆盖
依赖 numpy scipy matplotlib

sklearn

依赖库：numpy scipy matplotlib

数据集

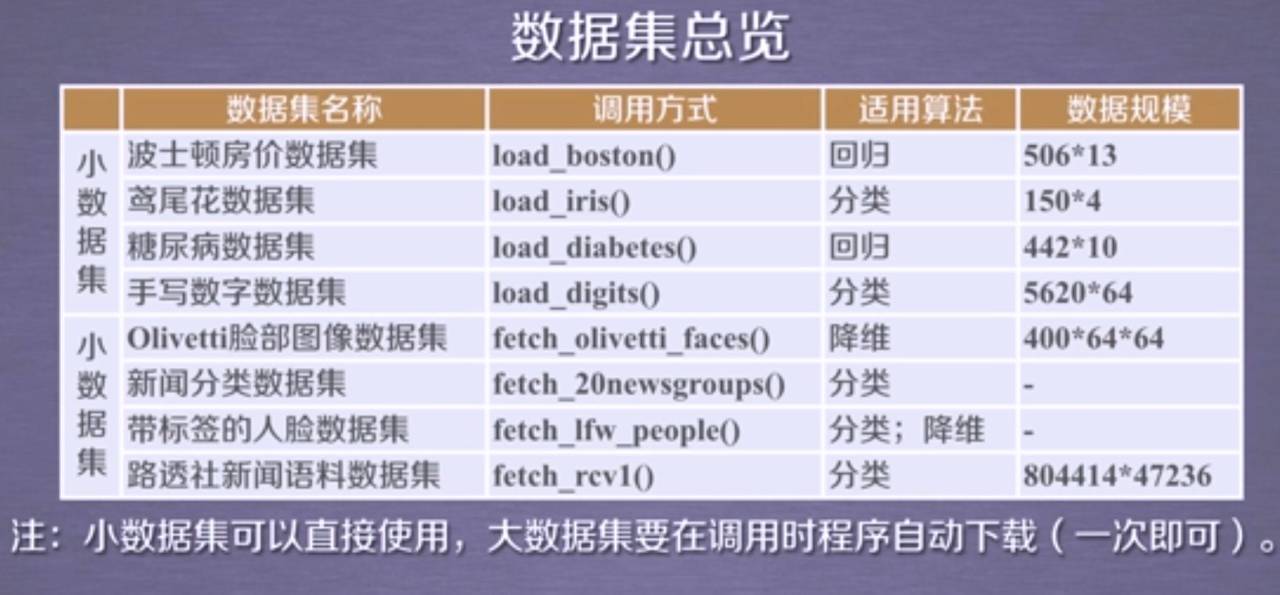
QQ图片20200317203238.jpg
波士顿房价数据集
506组信息，每条包括房屋以及房屋周围的详细信息：犯罪率、一氧化氮浓度、住宅平均房间数、到中心的加权距离、自住房平均房价。（回归问题）

  1. from sklearn.datasets import load_boston
  2. boston=load_boston()
  3. print(boston.data.shape)
  5. #(506,13)
  6. ###
  7. 重要参数：
  8. (return_X_y=True)，是否返回target(价格)
  9. 缺省为False  只返回data（属性）
  11. ###
  12. from sklearn.datasets import load_boston
  13. data,target=load_boston(return_X_y=True)
  14. print(data.shape)
  15. print(target.shape)
  17. #(506, 13)
  18. (506,)

鸢尾花数据集

  1. 重要参数：
  2. (return_X_y=True)，则以（data,target）形式返回数据；默认为False,表示以字典形式返回数据全部信息（包含data和target）
  6. from sklearn.datasets import load_iris
  7. iris=load_iris()
  8. print(iris.data.shape)
  9. print(iris.target.shape)
  10. print(list(iris.target_names))
  12. #(150, 4)
  13. (150,)
  14. ['setosa', 'versicolor', 'virginica']

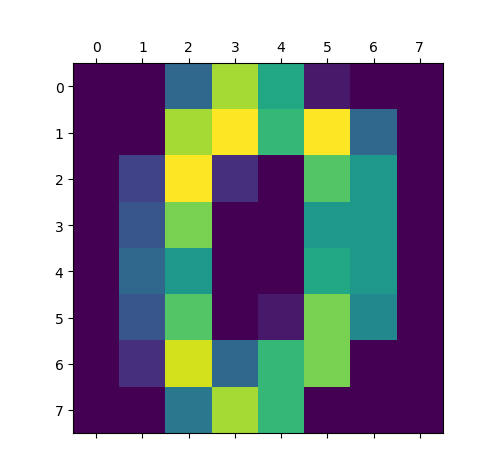
手写数字数据集
包含1797个0-9的手写数字数据，每个数字由8*8大小的矩阵构成，矩阵中值的范围是0-16，代表颜色的深度。

  1. 重要参数：
  2. (return_X_y=True)，则以（data,target）形式返回数据；默认为False,表示以字典形式返回数据全部信息（包含data和target）
  3. 特别属性
  4. n_class：表示返回数据的类别数，如n_class=5，则返回0到4的数据样本
  7. from sklearn.datasets import load_digits
  8. digits=load_digits()
  9. import matplotlib.pyplot as plt
  10. plt.matshow(digits.images[0])
  11. plt.show()

Figure_1.png

分类

异常检测、图像识别
**分类.png

聚类

图像分割、群体划分
sklearn.cluster模块
标准数据输入格式：[样本个数，特征个数]定义的矩阵形式
**聚类.png
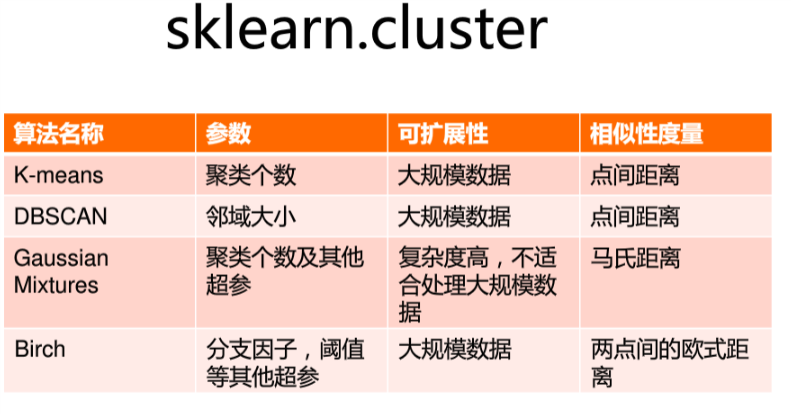
草图.png

K-means

以K为参数，把n个对象分为k个簇，使簇内具有较高的相似度，而簇间的相似度较低
随机选择K个点作为初始聚类中心
对剩下的点根据与聚类中心的距离，将其归入最近的簇
对每个簇计算所有点的均值作为新的聚类中心
重复上述两个步骤直到中心不再改变，得到最终的簇
1.png2.png3.png

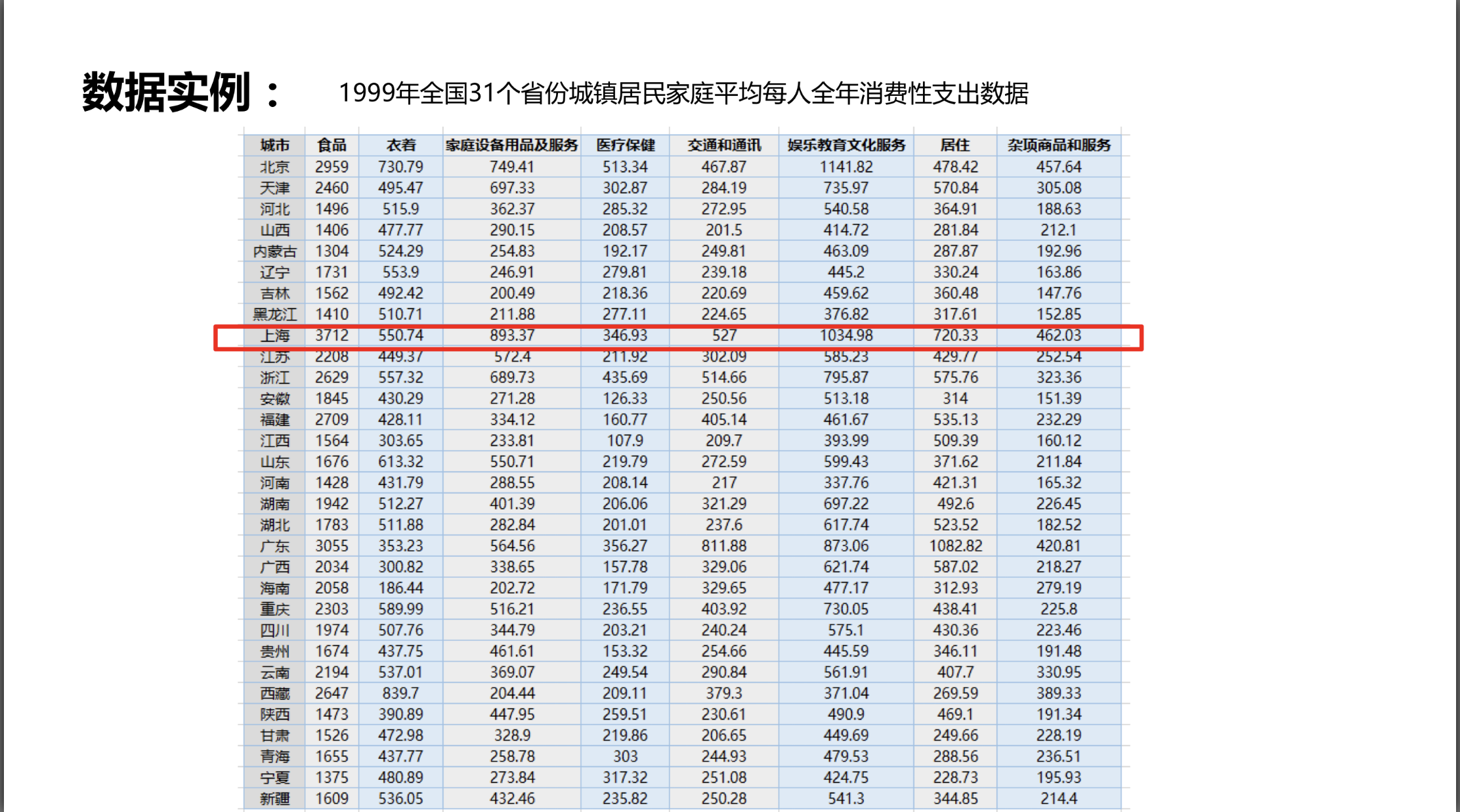
按照消费水平对城市聚类（1999）

  1. import numpy as np 
  2. from sklearn.cluster import KMeans
  3. def loadData(filePath):
  4.     fr=open(filePath,'r+',encoding='UTF-8')
  5.     lines=fr.readlines()
  6.     retData=[]
  7.     retCityName=[]
  8.     for line in lines:
  9.         items=line.strip().split(",")#去除头尾的空格，按“，”分割
  10.         retCityName.append(items[0])
  11.         retData.append([float(items[i]) for i in range(1,len(items))])        
  12.     return retData,retCityName
  17. data,cityname=loadData('D:/anaconda/workspace/baidubaike/machine_learning/city.txt')#利用loaddata方法读取数据
  18. km=KMeans(n_clusters=3)#指定聚类中心的个数
  19. #init:初始聚类中心的初始化方法
  20. #max_iter:最大迭代次数
  21. #一般init默认为k-means++,max_iter默认为300
  22. label=km.fit_predict(data)#创建KMeans方法实例进行训练，获得标签（label）
  23. #fit_predict():计算簇中心以及为簇分配序号
  24. print('label')
  25. print(label)
  26. #可以看出这里创建了0、1、2三个簇
  27. expenses=np.sum(km.cluster_centers_,axis=1)
  28. print('打印结果：')
  29. CityCluster=[[],[],[]]#分成三个簇
  30. for i in range(len(cityname)):
  31.     CityCluster[label[i]].append(cityname[i])
  32. for i in range(len(CityCluster)):
  33.     print("Expenses:%.2f"%expenses[i])
  34.     print(CityCluster[i])

得到
label
[2 1 0 0 0 0 0 0 2 1 1 0 1 0 0 0 1 0 2 1 1 1 1 0 1 1 0 0 0 0 0]
打印结果：
Expenses:3827.87
['河北', '山西', '内蒙古', '辽宁', '吉林', '黑龙江', '安徽', '江西', '山东', '河南', '湖北', '贵州', '陕西', '甘肃', '青海', '宁夏', '新疆']
Expenses:5113.54
['天津', '江苏', '浙江', '福建', '湖南', '广西', '海南', '重庆', '四川', '云南', '西藏']
Expenses:7754.66
['北京', '上海', '广东']

DBSCAN

基于密度进行聚类的算法
不需要预先指定簇的个数
最终簇的个数也不确定
将数据点分为三类：
核心点：在半径Eps内含有超过MinPts数目的点
边界点：在半径Eps内点的数量小于MinPts，但是落在核心点的领域内
噪声点：两者皆不是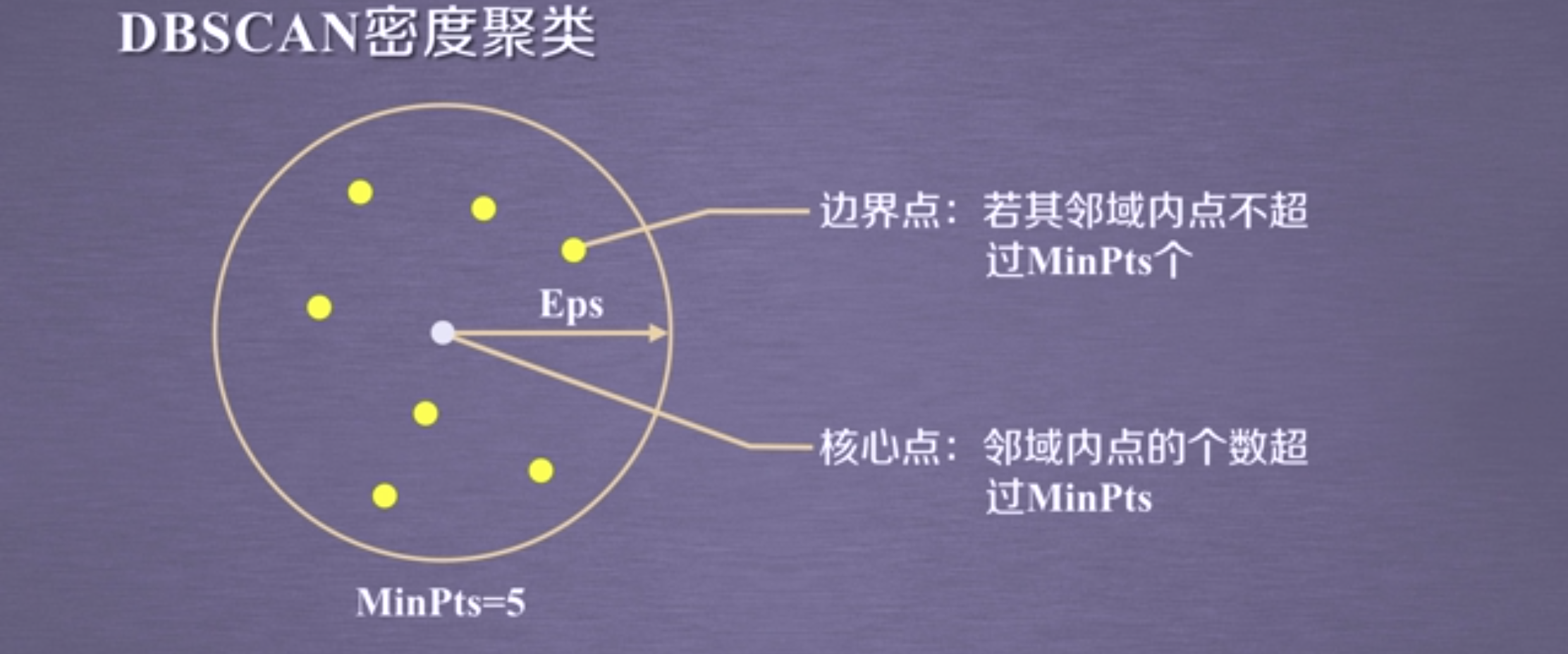
密度聚类.png
算法流程：
将所有点标记为三者之一（先确定核心点，再确定边界点和噪声点）
删除噪声点
将距离不超过Eps的点相互连接，构成一个簇，核心点领域内的点也会被加入这个簇中

分析学生上网时间和上网时长

实例.png
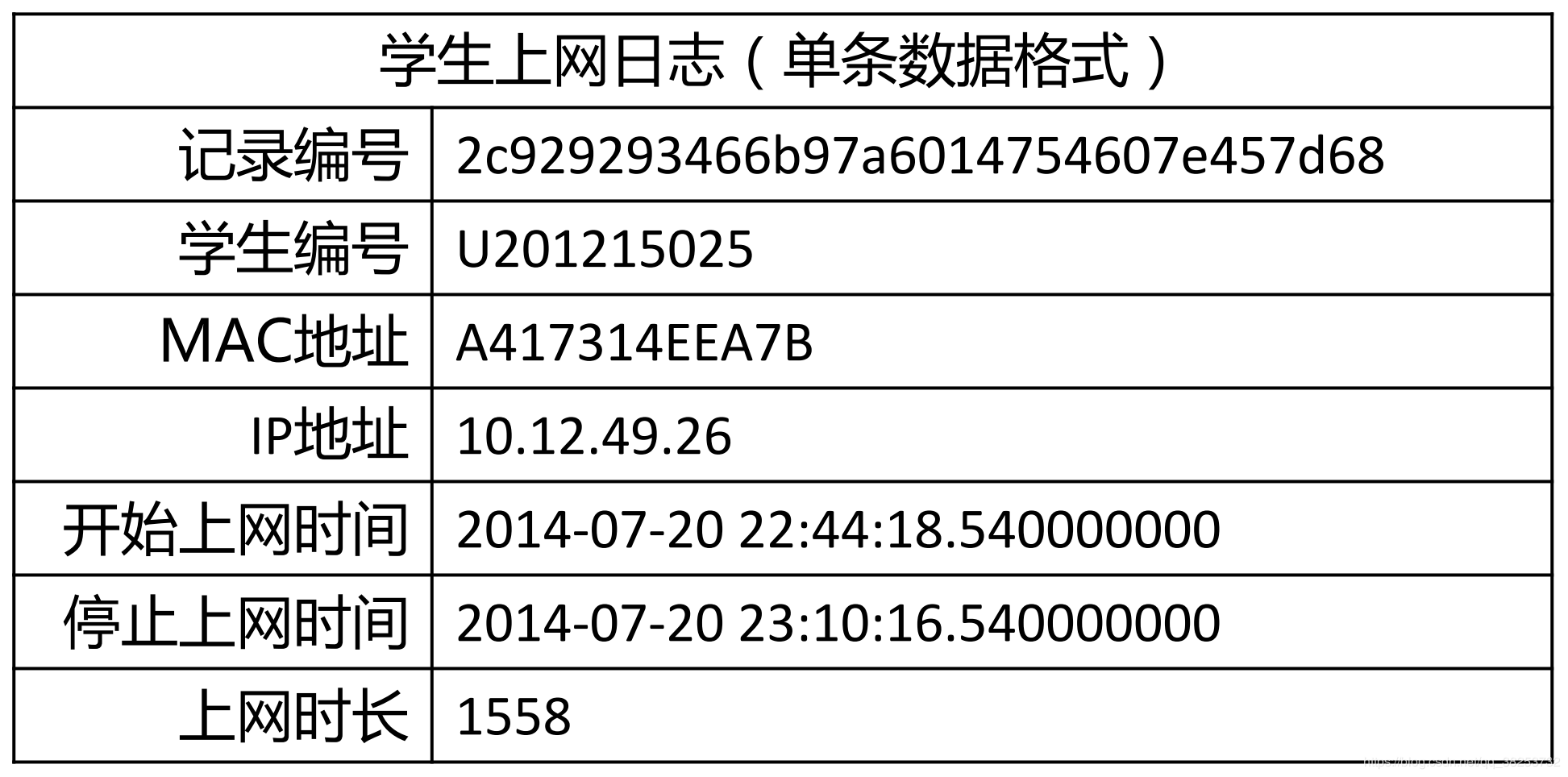
数据内容.png
对上网开始时间进行聚类

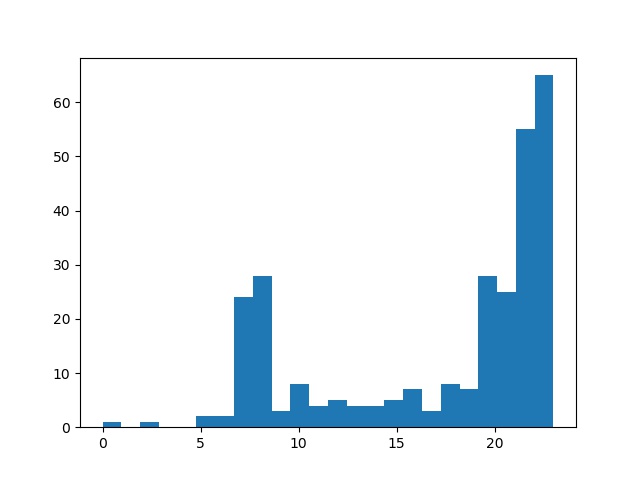
  1. import numpy as np
  2. import sklearn.cluster as skc
  3. from sklearn import metrics
  4. import matplotlib.pyplot as plt
  6. #DBSCAN主要参数：eps：两个样本被看作邻居节点的最大距离，min_samples:簇的样本数，metric；距离的计算方式（欧式距离：euclidean）
  8. mac2id=dict()
  9. onlinetimes=[]
  10. f=open('D:/anaconda/workspace/baidubaike/machine_learning/onlinetime_TestData.txt',encoding='utf-8')
  11. for line in f:
  12.     mac=line.split(',')[2]
  13.     onlinetime=int(line.split(',')[6])
  14.     starttime=int(line.split(',')[4].split(' ')[1].split(':')[0])#读取每条数据中的mac地址，开始上网时间，上网时长
  15.     if mac not in mac2id:
  16.         mac2id[mac]=len(onlinetimes)
  17.         onlinetimes.append((starttime,onlinetime))
  18.     else:
  19.         onlinetimes[mac2id[mac]]=[(starttime,onlinetime)]#mac2id是一个字典，key就是mac地址，value对应的就是上网时长和开始时间
  20. real_X=np.array(onlinetimes).reshape((-1,2))#参数-1可以自动确定行数
  22. X=real_X[:,0:1]# 截取第一列
  24. db=skc.DBSCAN(eps=0.01,min_samples=20).fit(X)
  25. labels = db.labels_#调用DBSCAN,labels为每个数据的簇标签
  27. print('Labels:')
  28. print(labels)
  29. raito=len(labels[labels[:] == -1]) / len(labels)#标签为-1，意味着其为噪声数据
  30. print('Noise raito:',format(raito, '.2%'))
  32. n_clusters_ = len(set(labels)) - (1 if -1 in labels else 0)#簇的个数
  34. print('Estimated number of clusters: %d' % n_clusters_)
  35. print("Silhouette Coefficient: %0.3f"% metrics.silhouette_score(X, labels))
  36.  #轮廓系数（Silhouette Coefficient）的值是介于 [-1,1] ，越趋近于1代表内聚度和分离度都相对较优
  37. for i in range(n_clusters_):
  38.     print('Cluster ',i,':')
  39.     print(list(X[labels == i].flatten()))
  40. # flatten()方法:将numpy对象（如array、mat）折叠成一维数组返回     
  41. plt.hist(X,24)#直方图
  42. plt.savefig('DBSCAN.jpg')

Labels:[ 0 -1 0 1 -1 1 0 1 2 -1 1 0 1 1 3 -1 -1 3 -1 1 1 -1 1 3 4 -1 1 1 2 0 2 2 -1 0 1 0 0 0 1 3 -1 0 1 1 0 0 2 -1 1 3 1 -1 3 -1 3 0 1 1 2 3 3 -1 -1 -1 0 1 2 1 -1 3 1 1 2 3 0 1 -1 2 0 0 3 2 0 1 -1 1 3 -1 4 2 -1 -1 0 -1 3 -1 0 2 1 -1 -1 2 1 1 2 0 2 1 1 3 3 0 1 2 0 1 0 -1 1 1 3 -1 2 1 3 1 1 1 2 -1 5 -1 1 3 -1 0 1 0 0 1 -1 -1 -1 2 2 0 1 1 3 0 0 0 1 4 4 -1 -1 -1 -1 4 -1 4 4 -1 4 -1 1 2 2 3 0 1 0 -1 1 0 0 1 -1 -1 0 2 1 0 2 -1 1 1 -1 -1 0 1 1 -1 3 1 1 -1 1 1 0 0 -1 0 -1 0 0 2 -1 1 -1 1 0 -1 2 1 3 1 1 -1 1 0 0 -1 0 0 3 2 0 0 5 -1 3 2 -1 5 4 4 4 -1 5 5 -1 4 0 4 4 4 5 4 4 5 5 0 5 4 -1 4 5 5 5 1 5 5 0 5 4 4 -1 4 4 5 4 0 5 4 -1 0 5 5 5 -1 4 5 5 5 5 4 4]
Noise raito:22.15%Estimated number of clusters:6Silhouette Coefficient: 0.710Cluster 0 :[22, 22, 22, 22, 22, 22, 22, 22, 22, 22, 22, 22, 22, 22, 22, 22, 22, 22, 22, 22, 22, 22, 22, 22, 22, 22, 22, 22, 22, 22, 22, 22, 22, 22, 22, 22, 22, 22, 22, 22, 22, 22, 22, 22, 22, 22, 22, 22, 22, 22, 22, 22, 22, 22, 22]
Cluster 1 :[23, 23, 23, 23, 23, 23, 23, 23, 23, 23, 23, 23, 23, 23, 23, 23, 23, 23, 23, 23, 23, 23, 23, 23, 23, 23, 23, 23, 23, 23, 23, 23, 23, 23, 23, 23, 23, 23, 23, 23, 23, 23, 23, 23, 23, 23, 23, 23, 23, 23, 23, 23, 23, 23, 23, 23, 23, 23, 23, 23, 23, 23, 23, 23, 23]
Cluster 2 :[20, 20, 20, 20, 20, 20, 20, 20, 20, 20, 20, 20, 20, 20, 20, 20, 20, 20, 20, 20, 20, 20, 20, 20, 20, 20, 20, 20]
Cluster 3 :[21, 21, 21, 21, 21, 21, 21, 21, 21, 21, 21, 21, 21, 21, 21, 21, 21, 21, 21, 21, 21, 21, 21, 21, 21]
Cluster 4 :[8, 8, 8, 8, 8, 8, 8, 8, 8, 8, 8, 8, 8, 8, 8, 8, 8, 8, 8, 8, 8, 8, 8, 8, 8, 8, 8, 8]Cluster 5 :
[7, 7, 7, 7, 7, 7, 7, 7, 7, 7, 7, 7, 7, 7, 7, 7, 7, 7, 7, 7, 7, 7, 7, 7]

DBSCAN.jpg

基于聚类的图像分割

图像分割
利用图像的灰度、颜色、纹理、形状等特征，把图像分成若 干个互不重叠的区域，并使这些特征在同一区域内呈现相似性，在不同的区 域之间存在明显的差异性。然后就可以将分割的图像中具有独特性质的区域 提取出来用于不同的研究。
图像分割常用方法
阈值分割：对图像灰度值进行度量，设置不同类别的阈值，达到分割的目的。
边缘分割：对图像边缘进行检测，即检测图像中灰度值发生跳变的地方，则为一片 区域的边缘。
直方图法：对图像的颜色建立直方图，而直方图的波峰波谷能够表示一块区域的颜 色值的范围，来达到分割 的目的。
特定理论：基于聚类分析、小波变换等理论完成图像分割。
目标
利用K-means聚类算法对图像像素点颜色进行聚类实现简单的图像分割
输出
同一聚类中的点使用相同颜色标记，不同聚类颜色不同

  1. import numpy as np
  2. import PIL.Image as image
  3. from sklearn.cluster import KMeans
  5. def loadData(filePath):
  6.     f = open(filePath,'rb')
  7.     data = []
  8.     img = image.open(f)
  9.     m,n = img.size
  10.     for i in range(m):
  11.         for j in range(n):
  12.             x,y,z = img.getpixel((i,j))
  13.             data.append([x/256.0,y/256.0,z/256.0])
  14.     f.close()
  15.     return np.mat(data),m,n
  17. imgData,row,col = loadData('D:/360MoveData/Users/lenovo/Desktop/bull.jpg')
  18. label = KMeans(n_clusters=4).fit_predict(imgData)
  20. label = label.reshape([row,col])
  21. pic_new = image.new("L", (row, col))
  22. for i in range(row):
  23.     for j in range(col):
  24.         pic_new.putpixel((i,j), int(256/(label[i][j]+1)))
  25. pic_new.save("result-bull-4.jpg", "JPEG")

结果
bull.jpgresult-bull-4.jpg

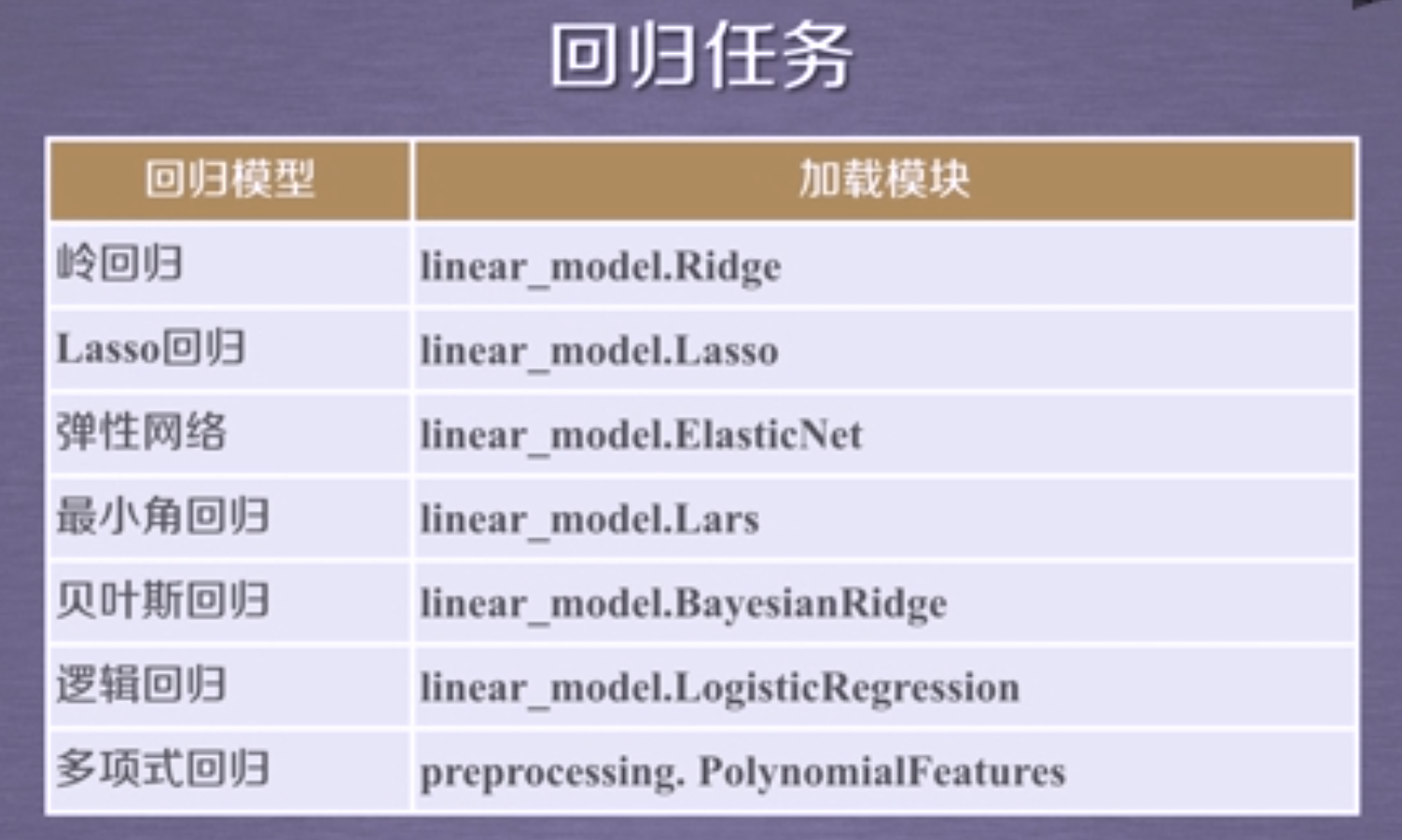
回归

价格预测、趋势预测
**回归.png

降维

可视化
降维过程可以理解为对数据集的组成成分进行分解（decomposition）的过程
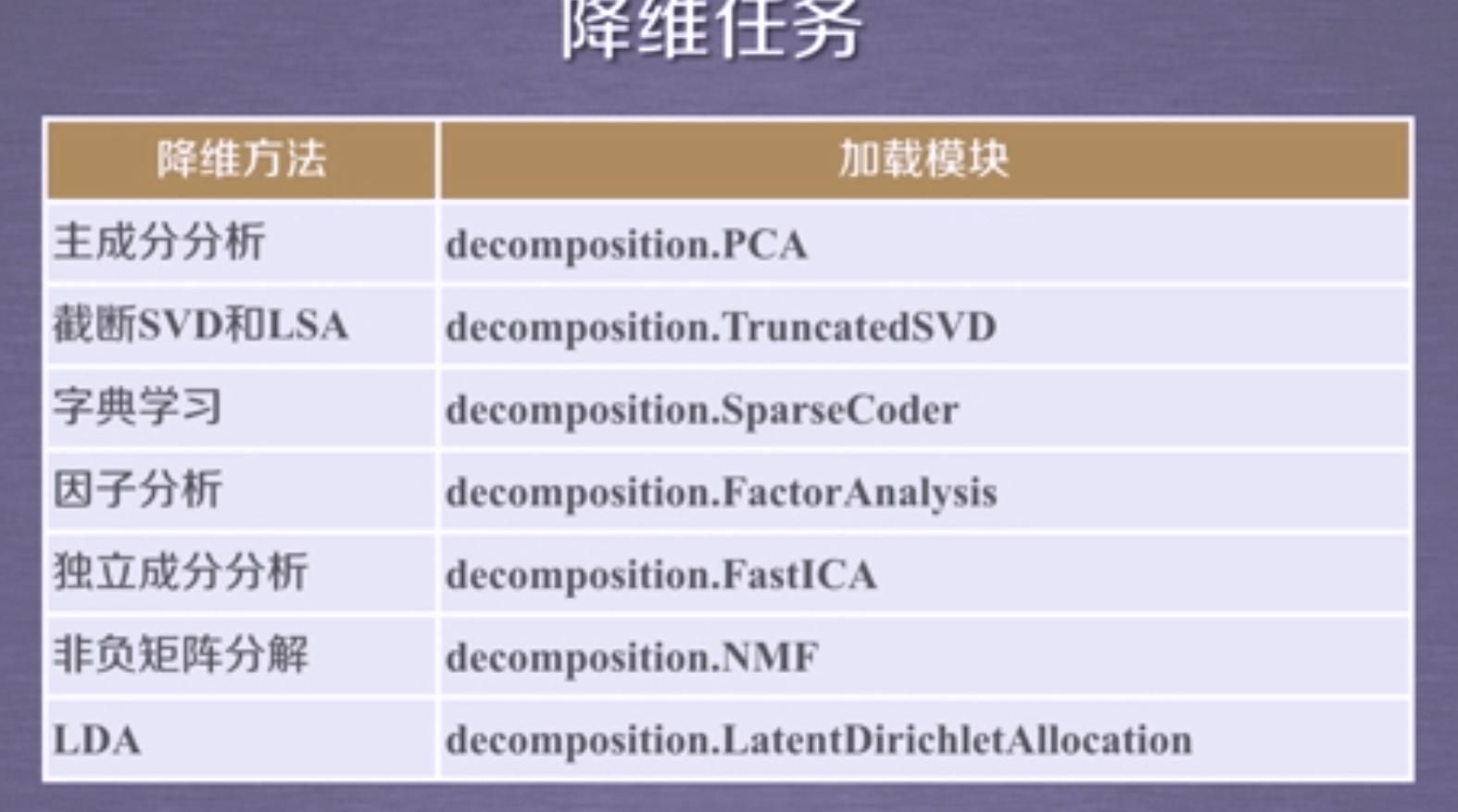
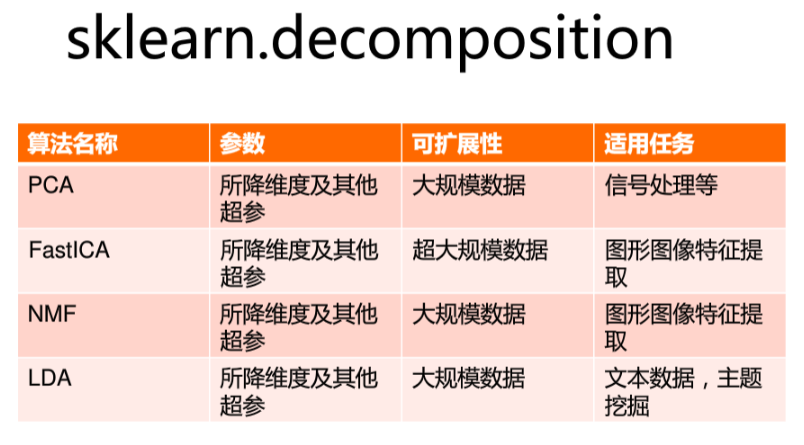
sklearn.decomposition
**降维.png
###草图.png

PCA

主成分分析（Principal Component Analysis）是常用的一种降维方法，高维数据集的探索和可视化，数据压缩和预处理
把具有相关性的高维变量合成为线性无关的低维变量，称为主成分。尽可能保留原有信息
术语：方差、协方差、特征向量
原理:矩阵的主成分就是其协方差矩阵对应的特征向量，按照对应的特征值大小进行排序，最大特征值就是第一主成分，其次为第二主成分，以此类推
算法过程
**草图.png

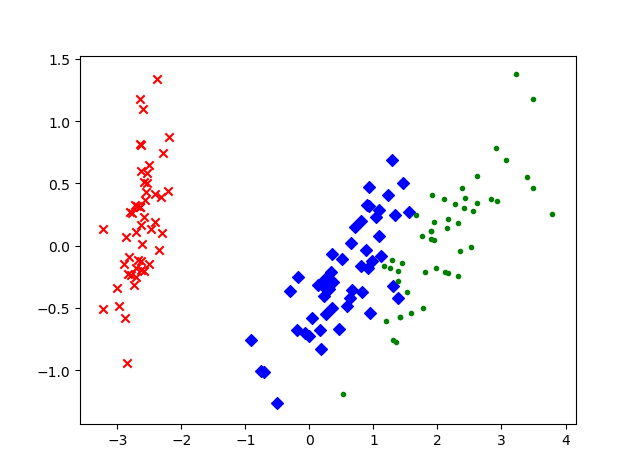
鸢尾花数据的二维平面的可视化

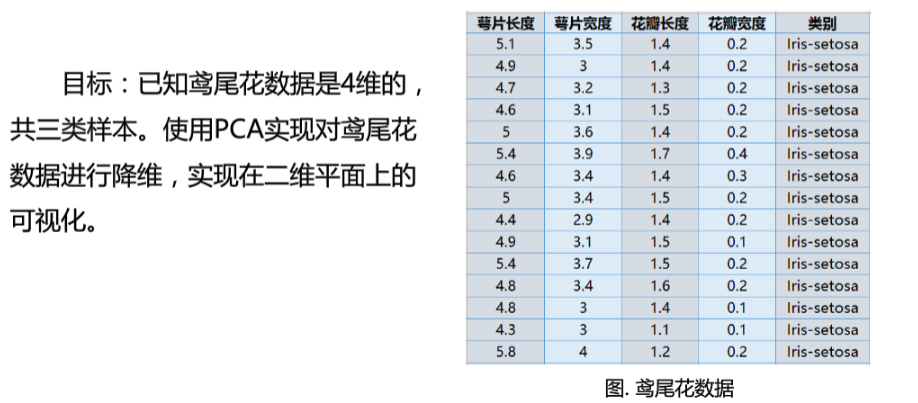
草图.png 

  1. #n_components:指定主成分的个数，即降维后数据的维度
  2. #svd_solver:设置特征值分解的方法，默认为'auto',其他：'full','arpack','randomized'
  3. import matplotlib.pyplot as plt 
  4. from sklearn.decomposition import PCA
  5. from sklearn.datasets import load_iris
  7. data = load_iris()
  8. #以字典形式加载鸢尾花数据集
  9. y = data.target #使用y表示数据集中的标签
  10. X = data.data #使用X表示数据集中的属性数据
  11. pca = PCA(n_components=2)
  12. #加载PCA算法，设置降维后主成分数目为2
  13. reduced_X = pca.fit_transform(X)
  14. #对原始数据进行降维，保存在reduced_X中
  15. red_x, red_y = [], []
  16. #第一类数据点
  17. blue_x, blue_y = [], []
  18. #第二类数据点
  19. green_x, green_y = [], []
  20. #第三类数据点
  21. for i in range(len(reduced_X)):
  22.     if y[i]==0:
  23.         red_x.append(reduced_X[i][0])
  24.         red_y.append(reduced_X[i][1])
  25.     elif y[i]==1:
  26.         blue_x.append(reduced_X[i][0])
  27.         blue_y.append(reduced_X[i][1])
  28.     else:
  29.          green_x.append(reduced_X[i][0])
  30.          green_y.append(reduced_X[i][1])   
  31. plt.scatter(red_x, red_y, c='r', marker='x')
  32. #第一类数据点
  33. plt.scatter(blue_x, blue_y, c='b', marker='D')
  34. #第二类数据点
  35. plt.scatter(green_x, green_y, c='g', marker='.')
  36. #第三类数据点
  37. plt.show()
  38. #可视化

NMF

Figure_1.png

NMF

非负矩阵分解，在矩阵中所有元素均为非负数约束条件下的矩阵分解方法
给定一个非负矩阵V,NMF能够找到一个非负矩阵W和一个非负矩阵H，使得矩阵W和H的乘积近似等于V中的值
图像分析 文本挖掘 语音处理
目标：最小化V与WH的差

人脸数据特征提取

  1. #n_components:用于指定分解后矩阵的单个维度k
  2. #init:W H的初始化方式
  3. #通过设置k的大小，设置提取的特征的数目
  5. import matplotlib.cm as cm
  6. import matplotlib.pyplot as plt
  7. from sklearn import decomposition
  8. #加载PCA算法包
  9. from  sklearn.datasets import fetch_olivetti_faces
  10. #加载人脸数据集
  11. from numpy.random import RandomState
  12. #加载RandomState用于创建随机种子
  17. n_row,n_col = 2,3
  18. #设置图像展示时的排列情况，2行三列
  19. n_components = n_row*n_col
  20. #设置提取的特征的数目
  21. image_shape = (64,64)
  22. #设置人脸数据图片的大小
  24. dataset = fetch_olivetti_faces(shuffle=True,random_state=RandomState(0))
  25. faces = dataset.data#加载数据，并打乱顺序
  27. def plot_gallery(title,images,n_col=n_col,n_row=n_row):
  28.     plt.figure(figsize=(2. * n_col,2.26 * n_row))#创建图片，并指定大小
  29.     plt.suptitle(title,size=16)#设置标题及字号大小
  30.     for i,comp in enumerate(images):
  31.         plt.subplot(n_row,n_col,i+1)#选择画制的子图
  32.         vmax = max(comp.max(),-comp.min())
  33.         plt.imshow(comp.reshape(image_shape), cmap=cm.gray,
  34.                    interpolation='nearest', vmin=-vmax, vmax=vmax)#对数值归一化，并以灰度图形式显示
  35.         plt.xticks(())
  36.         plt.yticks(())#去除子图的坐标轴标签
  37.     plt.subplots_adjust(0.01,0.05,0.99,0.93,0.04,0.)
  40. estimators=[('Eigenfaces - PCA using randomized SVD',decomposition.PCA(n_components=6,whiten=True)),('Non-negative components - NMF',decomposition.NMF(n_components=6,init='nndsvda',tol=5e-3))]
  41. #NMF和PCA实例，将它们放在一个列表中
  44. for name,estimators in estimators:#分别调用PCA和NMF
  45.     estimators.fit(faces)#调用PCA或NMF提取特征
  46.     components_=estimators.components_#获取提取特征
  47.     plot_gallery(name,components_[:n_components])
  48.     #按照固定格式进行排列
  49. plt.show()#可视化

推荐书籍

机器学习-周志华 入门书籍
PRML-Bishop 贝叶斯学派
Machine Learning-Andrew Ng Coursera
**

TIPS

解决vscode中 输出框中文乱码：在我的电脑中添加环境变量 PYTHONIOENCODING 为 UTF8
解决Rstdio的console中文乱码 Sys.setlocale(“LC_ALL”,”Chinese)