97. 交错字符串

题意：

解题思路：

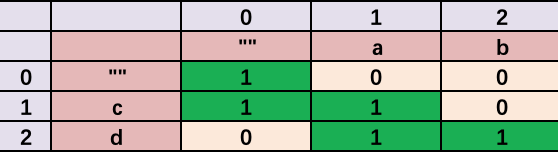
1. 状态定义：dp[i][j]表示s1的前i个字符和s2的前j个字符是否能构成s3的前i+j个字符； 
2. 初始化条件：dp[0][0] = true, s1,s2,s3的长度分别为len1,len2,len3
3. 初始化第一列dp[i][0]，遍历第一列，遍历区间[1,len1+1];
  dp[i][0] = dp[i - 1][0] && s1[i - 1] == s3[i - 1]:
  表示s1的前i位是否能构成s3的前i位,因此需要满足的条件为，前i−1位可以构成s3的前i−1位且s1的第i位          （s1[i−1]）等于s3的第i位（s3[i−1]）
  好比 s1:ab[0,1] => s3:acbd[0,1,2,3]=>
        (dp[0][0] && s1[0] == s3[0]) => dp[1][0] => true
4. 初始化第一行dp[0][j]，遍历第一行，遍历区间[1,len2+1]：
    dp[0][i]=dp[0][i−1] && s2[i−1]==s3[i−1]。
    表示s2的前i位是否能构成s3的前i位。因此需要满足的条件为，
    前i−1位可以构成s3的前i−1位且s2的第i位（s2[i-1]）等于s3的第i位（s3[i-1]）
5. 遍历dp数组，每一行i，遍历区间[1,len1+1]：
    每一列j，遍历区间[1,len2+1]
    dp[i][j] = (dp[i - 1][j] && s1[i - 1] == s3[i - 1 + j]) 
    || (dp[i][j - 1] && s2[j - 1] == s3[j - 1 + i]);
    解释：$s1前i位和s2的前j位能否组成s3的前i+j位取决于两种情况：
    s1的前i个字符和s2的前j−1个字符能否构成s3的前i+j−1位，
    且s2的第j位（s2[j−1]）是否等于s3的第i+j位（s3[i+j−1]）
    举例说明：
    s1 = 'ab' s2 = 'cd' s3 = 'acbd' =》dp[i][j - 1]=》 
    如果s1的第一个字符a等于s3的第一个字符a，那么只需要判断s2的j-1个字符c是否等于s3的j-1+i个字符
    当i,j=1的时候s2[j-1] = c, s3[j-i+1] = c,
    所以dp[1][1] = true : 表示s1的a 加s2的c能构成s3的i+j-1位字符ac

图示：

PHP代码实现：

class Solution {
    /**
     * @param String $s1
     * @param String $s2
     * @param String $s3
     * @return Boolean
     */
    function isInterleave($s1, $s2, $s3) {
        $m = strlen($s1);
        $n = strlen($s2);
        if ($m + $n != strlen($s3)) return false;
        $dp = [];
        $dp[0][0] = true;
        for ($i = 1; $i <= $m; $i++) {
            $dp[$i][0] = $dp[$i - 1][0] && $s1[$i - 1] == $s3[$i - 1];
        }
        for ($i = 1; $i <= $n; $i++) {
            $dp[0][$i] = $dp[0][$i - 1] && $s2[$i - 1] == $s3[$i - 1];
        }
        for ($i = 1; $i <= $m; $i++) {
            for ($j = 1; $j <= $n; $j++) {
                $dp[$i][$j] = ($dp[$i - 1][$j] && $s1[$i - 1] == $s3[$i - 1 + $j]) 
                    || ($dp[$i][$j - 1] && $s2[$j - 1] == $s3[$j - 1 + $i]);
            }
        }
        return $dp[$m][$n];
    }
}

GO代码实现：

func isInterleave(s1 string, s2 string, s3 string) bool {
    m, n, n3 := len(s1), len(s2), len(s3)
    if m + n != n3 {
        return false
    }
    dp := make([][]bool, m+1)
    for i := range dp {
        dp[i] = make([]bool, n+1)
    }
    dp[0][0] = true
    for i := 1; i <= m; i++ {
        dp[i][0] = dp[i-1][0] && (s1[i-1] == s3[i-1])
    }
    for j := 1; j <= n; j++ {
        dp[0][j] = dp[0][j-1] && (s2[j-1] == s3[j-1])
    }
    for i := 1; i <= m; i++ {
        for j := 1; j <= n; j++ { 
            dp[i][j] = (dp[i-1][j] && s1[i-1] == s3[i+j-1]) ||
                (dp[i][j-1] && s2[j-1] == s3[i+j-1])
        }
    }
    return dp[m][n]
}