115. 不同的子序列

题意：

图示：

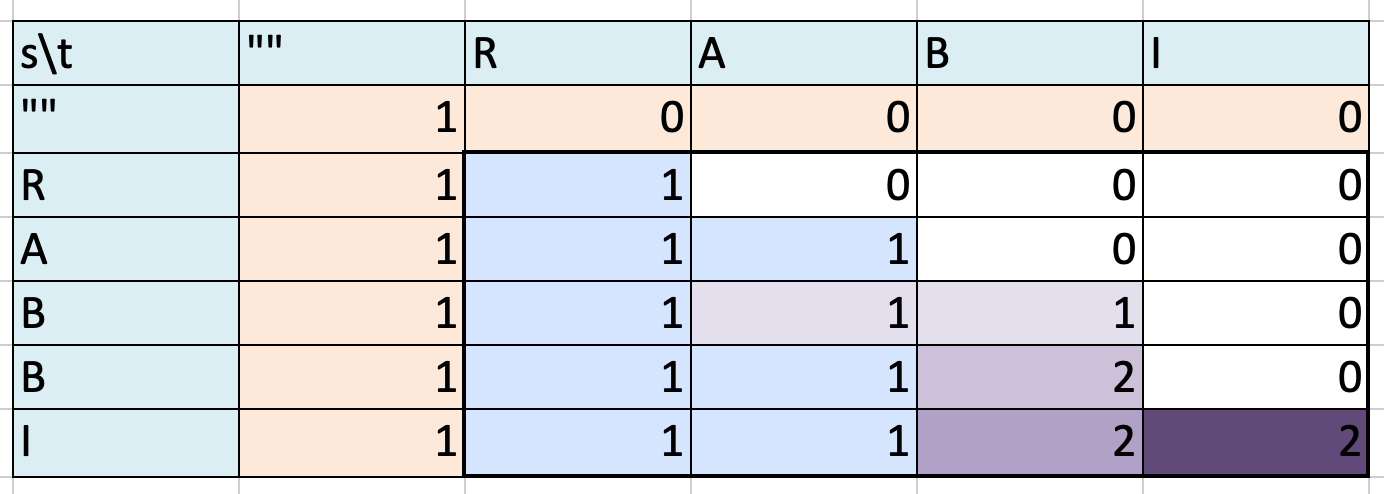
解题思路：

思路：
状态定义：dp[i][j]表示：s的前i个字符的子序列中，包含多少个t的前 j 个字符子串
转移方程：1. s[i-1]==t[j-1]时
    1.1 保留s[i-1]，有dp[i-1][j-1]种方法，即：确定s的第i个字符与t的第j个字符对应后，s的前 i-1 个字符有多少种方法变为t的前 j-1 个字符。
    1.2 比如：s = 'rabb' t = 'rab' 保留s跟t中的最后一个b，看前面s中rab是否可以组成多少个t中的ra，答案是一个
    1.3 不保留s[i-1]，有dp[i-1][j]种方法。即：不使用s的第i个字符，s的前 i-1 个字符有多少种方法变为t的前 j 个字符。
    1.4 比如：s = 'rabb' t = 'rab' 不保留s中的最后一个b，我们看s中的rab是否可以组成多少个t中的rab，答案也是一个
    最终，s[i-1]==t[j-1]时，dp[i][j] = dp[i-1][j-1]+dp[i-1][j]
2. s[i-1] != t[j-1]时，有dp[i-1][j]种方法,即：已知s的第 i 个字符不能与t的第 j 个字符对应，s的前 i-1 个字符有多少种方法变为t的前 j 个字符。
    比如 s = 'ra' t = 'r' 当s中的a不等于t中的r时，我们看s中除了a前面有几个可以组成t的可能性，即dp[i-1][j]

PHP代码实现：

class Solution {
    /**
     * @param String $s
     * @param String $t
     * @return Integer
     */
    function numDistinct($s, $t) {
        $dp = [];
        for ($i = 0; $i <= strlen($s); $i++) {
            //$t是空字符串的情况,空字符串也是s的子串
            $dp[$i][0] = 1;
        }
        for ($i = 1; $i <= strlen($t); $i++) {
            $dp[0][$i] = 0;//s为空,那就没办法匹配了
        }
        for ($i = 1; $i <= strlen($s); $i++) {
            for ($j = 1; $j <= strlen($t); $j++) {
                if ($s[$i-1] == $t[$j-1]) {
                    $dp[$i][$j] = $dp[$i - 1][$j - 1] + $dp[$i - 1][$j];
                } else {
                    $dp[$i][$j] = $dp[$i - 1][$j];
                }
            }
        }
        return $dp[strlen($s)][strlen($t)];
    }
}

GO代码实现：

func numDistinct(s string, t string) int {
    if len(s)==0  || len(s) < len(t) {
        return 0
    }
    dp := make([][]int, len(s)+1)
    for i := 0; i <= len(s); i++ {
        dp[i] = make([]int, len(s) + 1)
        dp[i][0] = 1
    }
    for i := 1;i <= len(s); i++ {
        for j := 1;j <= len(t); j++ {
            if s[i-1] == t[j-1] {
                dp[i][j] = dp[i-1][j-1] + dp[i-1][j]
            } else {
                dp[i][j] = dp[i-1][j]
            }
        }
    }
    return dp[len(s)][len(t)]
}