基于深度学习的推荐系统模型

FM模型理论

FM模型表示

普通的线性模型，我们都是将各个特征独立考虑的，并没有考虑到特征与特征之间的相互关系。但实际上，大量的特征之间是有关联的。FM主要是为了解决数据稀疏的情况下，特征怎样组合的问题。
一般的线性模型为：

显然一般的线性模型没有考虑特征间的关联。为了表述特征间的相关性，我们采用多项式模型。在多项式模型中，特征与的组合用表示：

组合部分的特征相关参数有个，在数据很稀疏时，和都不为0的情况非常少，导致无法通过训练得到。为了求解，FM的做法是把分解成两个向量<,>。直观来看，FM认为当一个特征考虑特征组合的时候，可以用一个k维向量来代表，而不需要针对所有的特征组合计算出组合参数，即通过用每一维特征的隐变量内积提取特征组合。

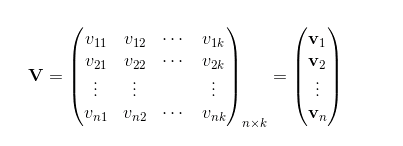
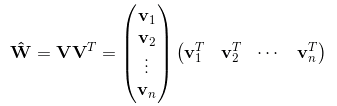
FM求解

带入y：

FFM模型理论

FFM模型中引入了field概念。简单来说，同一categorical特征经过one-hot编码生成的新特征属于同一field。
在FFM中，每一维特征，针对其他特征的每个field ，都会学习一个隐向量。因此隐向量不仅与特征有关，还有field有关。
假设样本的n个特征属于f个field，那么FM有n个隐向量，FFM有n*f个隐向量。FM可以看作FFM的特例，当所有特征都归属到一个field时，FFM即为FM。

DeepFM模型理论

基于CTR预估的推荐系统，最重要的是学习到用户点击行为背后隐含的特征组合。在不同的推荐场景中，低阶或高阶的特征组合可能都会对最终的CTR产生影响。
FM只用到了二阶特征组合，对于高阶特征组合，很自然的一个想法是通过多层神经网络即DNN去解决。

DNN的构架

对于离散特征的处理，我们使用的方法是将特征转换为one-hot向量。one-hot向量非常稀疏，如果直接输入到DNN中，会导致网络的参数过多。
解决思路是参考FFM中field的思想，将特征分field输入神经网络，经过一个嵌入层(embedding layer)，将one-hot转为低维稠密的向量。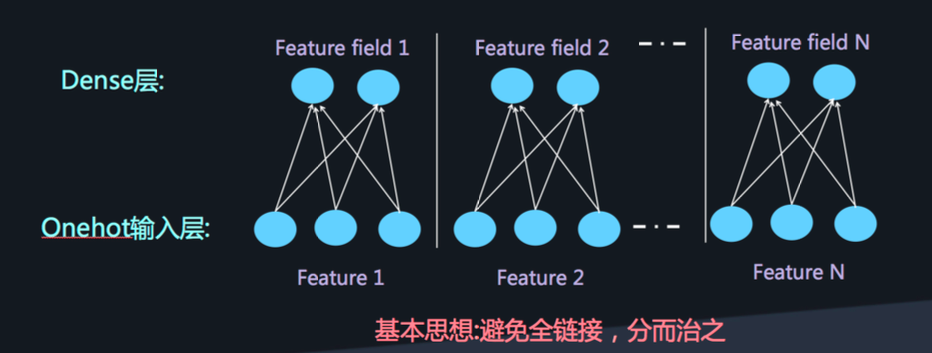

嵌入层得到的低维稠密的向量即为前馈神经网络的输入，再连接两个全连接层，就可以得到高阶特征组合。

FM+DNN

DeepFM将FM和DNN并行融合起来，FM和DNN的部分分别负责提取低阶和高阶的特征组合。这两个部分共享相同的输入，两部分输出相加后再经过一个sigmoid函数即为整个DeepFM的输出结果。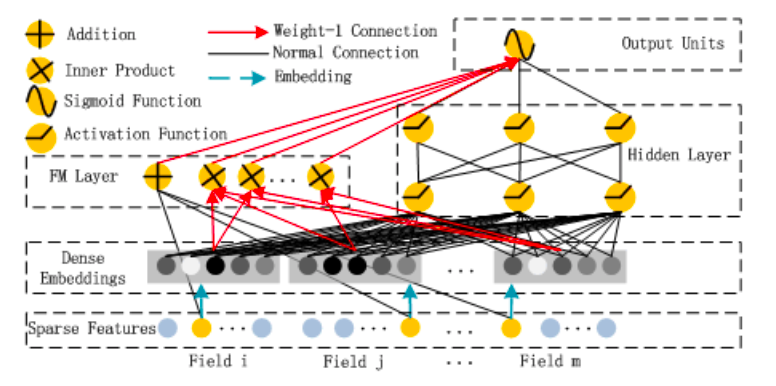

嵌入层有两个特点：

1. 尽管不同field的输入长度不同，但是embedding之后的长度均为k
2. 在FM中得到的隐变量V_ik作为了嵌入层的权重

对于第二点的理解：假设k=5，首先，对于输入的one-hot向量，同一个field 只有一个位置是1，那么在由输入到嵌入层的过程中，输入层只有一个位置的神经元被激活，得到的低维稠密向量其实就是输入层到嵌入层层该神经元相连的权重，即，，，，。这五个值组合起来就是FM中所提到的。在FM部分和DNN部分，权重是共享的，对同一个特征来说，得到的Vi是相同的。