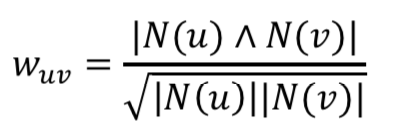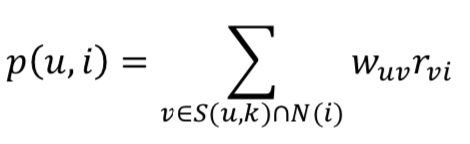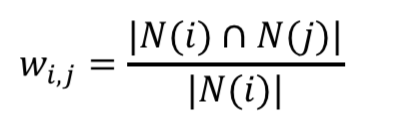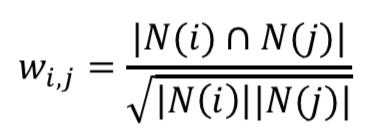用户行为分析
用户活跃度和物品流行度都呈长尾分布。且用户越活跃越倾向于浏览冷门的物品
协同过滤算法定义
用户齐心协力,通过不断和网站互动,使自己的推荐列表能够不断过滤掉自己不感兴趣的物品,从来越来越满足自己的需求
主要的协同过滤方法有:
- 基于邻域的方法:基于用户的协同过滤和基于物品的协同过滤
- 隐语义模型
-
基于邻域的算法
基于用户的协同过滤
主要步骤:
找到和目标用户兴趣相似的用户集合
找到这个集合中的用户喜欢的,且目标用户没有听说过的物品推荐给目标用户
用户相似度计算
用户u和用户v的相似度:
Jaccard相似度
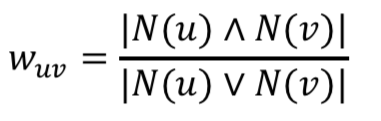
- 余弦相似度
用户对物品的感兴趣程度
用户相似度计算改进
两个用户对冷门物品采取过相同的行为更能说明他们兴趣的相似度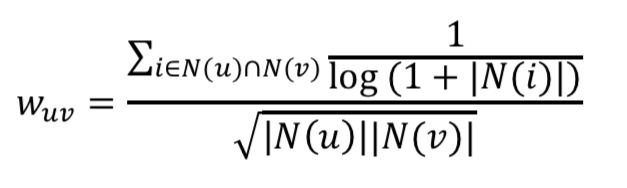
该公式惩罚了用户u和用户v共同兴趣列表中热门物品对他们相似对的影响
基于物品的协同过滤
通过分析用户的行为记录计算法物品之间的相似度。该算法认为物品A和物品B具有很大的相似度是因为喜欢物品A的用户大都也喜欢物品B。主要步骤:
活跃的用户对物品相似度的贡献应该小于不活跃的用户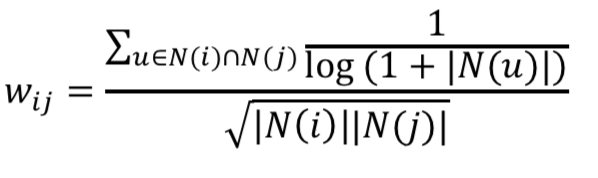
- 归一化
归一化可以提高推荐多样性和覆盖率的原因:热门的类的类内相似度一般较大,如果不进行补一化,就会偏向于推荐更加热门的类的物品
协同过滤的问题:两个不同领域的最热物品之间往往具有比较高的相似度,这时候仅靠用户的行为数据不能解决问题
代码示例
import numpy as npdef ItemSimilarity_alpha(data, alpha = 0.3):N = dict() # 书本被购买的用户数C = dict() # 书本被同时购买的用户数for u, items in data.items():for i in items.keys():if i not in N.keys():N[i] = 0N[i] += 1for j in items.keys():if i == j:continueif i not in C.keys():C[i] = dict()if j not in C[i].keys():C[i][j] = 0# 当用户购买了i和j:+1C[i][j] += 1W = dict()for i, related_items in C.items():if i not in W.keys():W[i] = dict()for j, cij in related_items.items():W[i][j] = cij / (np.power(N[i], alpha) * np.power(N[j], 1 - alpha))return W# 结合用户的喜好对物品排序def Recommend(train, user_id, W, K):rank = dict()ru = train[user_id]for i, pi in ru.items():tmp = W[i]for j, wj in sorted(tmp.items(), key=lambda d: d[1], reverse=True)[0:K]:if j in ru: # 如果用户已经购买过,则不再推荐continueif j not in rank.keys():rank[j] = 0rank[j] += pi * wj # 待推荐的物品j于用户已经购买过的物品i相似,则累加上相似的分数return rankif __name__ == '__main__':Train_Data = {'A': {'i1': 1, 'i2': 1, 'i4': 1},'B': {'i1': 1, 'i4': 1},'C': {'i1': 1, 'i2': 1, 'i5': 1},'D': {'i2': 1, 'i3': 1},'E': {'i3': 1, 'i5': 1},'F': {'i2': 1, 'i4': 1}}W = ItemSimilarity_alpha(Train_Data)rank = Recommend(Train_Data, 'C', W, 3)print(rank)
UserCF和ItemCF对比
| UserCF | ItemCF | |
|---|---|---|
| 性能 | 适用于用户较少的场合 | 适用于物品数明显少于用户数,且物品数据相对稳定的场合 |
| 领域 | 时效性强,内容更新频率高,用户个性化兴趣不太明显的领域,如新闻、博客等 | 长尾物品丰富,注重用户个性化需求的领域,如购物网站、图书、电影网站等 |
| 多样性 | UserCF的多样性不高 | ItemCF的多样性远好于UserCF,ItemCF更容易发现并推荐长尾物品 |
| 推荐解释 | 很难提供令用户信服的推荐解释 | 可以很方便地提供推荐解释,提高用户对推荐系统的信任度 |
基于矩阵分解的推荐方法
矩阵A是一个m*n的矩阵,定义矩阵A的SVD为:
在得到SVD矩阵分解之后,需要确定保留的奇异值数目,一个典型的做法是保留矩阵中90%的能量信息。如果选取最大的k个奇异值来描述矩阵A:
将AT映射到低维空间:
代码示例
import numpy as np
def loadExData():
return [[0, 0, 1, 0, 0, 2, 0, 0, 0, 0, 5],
[0, 0, 0, 5, 0, 3, 0, 0, 0, 0, 3],
[0, 0, 0, 0, 4, 1, 0, 1, 0, 4, 0],
[3, 3, 4, 0, 0, 0, 0, 2, 2, 0, 0],
[5, 4, 2, 0, 0, 0, 0, 5, 5, 0, 0],
[0, 0, 0, 0, 5, 0, 1, 0, 0, 0, 0],
[4, 1, 4, 0, 0, 0, 0, 4, 5, 0, 1],
[0, 0, 0, 4, 0, 4, 0, 0, 0, 0, 4],
[0, 0, 0, 2, 0, 2, 5, 0, 0, 1, 2],
[1, 0, 0, 4, 0, 0, 0, 1, 2, 0, 0]]
def cosSim(U_k, W_t):
num = float(U_k.T * W_t)
denom = np.linalg.norm(U_k) * np.linalg.norm(W_t)
return 0.5 + 0.5 * (num/denom)
def svdEst(userData, xformedItems, user, simMeas, item):
n = np.shape(xformedItems)[0]
simTotal = 0.0; ratSimTotal = 0.0
# 对于给定的用户,for循环所有的物品,计算与item的相似度
for j in range(n):
userRating = userData[:, j]
if userRating == 0 or j == item: continue
similarity = simMeas(xformedItems[item, :].T, xformedItems[j, :].T)
print('the %d and %d similarity is : %f ' %(item, j, similarity))
# 对相似度求和
simTotal += similarity
# 对相似度及评分值的乘积求和
ratSimTotal += similarity * userRating
if simTotal == 0: return 0
return ratSimTotal / simTotal
def recommend(dataMat, user, N=3, simMeas=cosSim, estMethod=svdEst):
U, sigma, VT = np.linalg.svd(dataMat)
# 使用奇异值构建对角矩阵
Sig4 = np.mat(np.eye(4) * sigma[:4])
# 将物品转换到低维空间
xformedItems = dataMat.T * U[:, :4] * Sig4.I
print('xformedItems=', xformedItems)
print('xformedItems的行数和列数', np.shape(xformedItems))
# np.nonzero返回数组中非零元素的索引值
unratedItems = np.nonzero(dataMat[user, :].A == 0)[1]
# 如果不存在未评分的物品,推出函数,否则在所有未评分物品上循环
if len(unratedItems) == 0:
print("you rated everything")
itemScores = []
for item in unratedItems:
print('item=', item)
# 对于每个未评分物品,通过调用standEst()来产生该物品基于相似度的预测评分
estimateScore = estMethod(dataMat[user, :], xformedItems, user, simMeas, item)
itemScores.append((item, estimateScore))
# 相似度最高的前N个未评级物品
return sorted(itemScores, key=lambda jj: jj[1], reverse=True)[:N]
if __name__ == '__main__':
myMat = np.mat(loadExData())
result = recommend(myMat, 1, estMethod=svdEst)
print('result: ', result)
隐语义分析(LFM)
基于用户行为统计自动聚类,计算出物品属于每个类的权重
LFM中用户u对物品i的兴趣:
通过优化如下损失函数来找到最合适的参数p和q: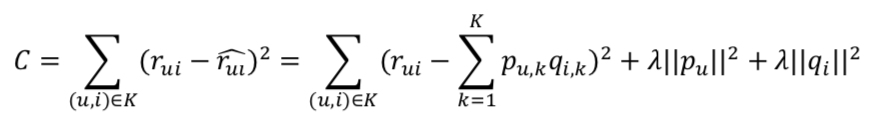
采用随机梯度下降,求参数的偏导数找到最快下降方向,通过迭代法不断优化参数直至参数收敛
隐语义分析的空间复杂度低,但是每次都需要通过梯度下降寻找最优解,因此时间复杂度高。此外,隐语义分析不能进行在线的实时推荐,也无法像基于物品的协同过滤一样提供模型的解释
基于图的模型
随机游走(PersonalRank算法)
从用户u节点开始在用户物品二分图上进行随机游走,游走到热和一个节点时,按照概率a决定继续游走,还是停止这次游走并从节点u重新游走。如果决定继续游走,那么就从当前节点中按照均匀分布随机选择一个节点作为下一个游走节点。经过多次随机游走,每个物品节点被访问到的概率会收敛到一个数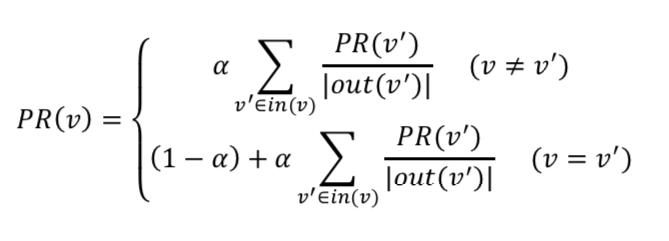
收敛的过程十分复杂,无法在线提供实时推荐,即使离线也很耗时