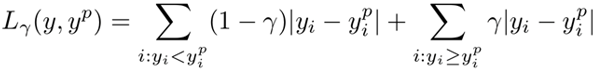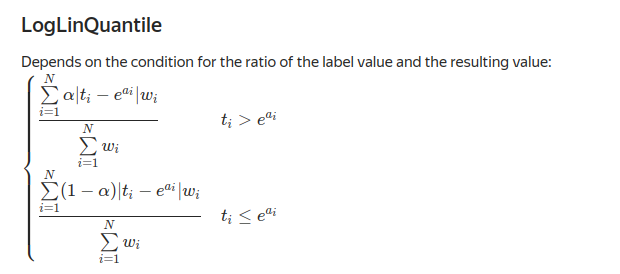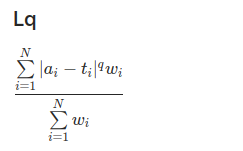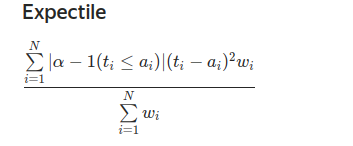- 1、均方误差:MSE(Mean Squared Error)- L2损失
- 3、平均绝对误差:MAE(Mean Absolute Error)
- 4. MAPE
- MAE vs MSE vs RMSE vs MAPE:
- 5. Huber loss -滑平均绝对误差
- 6 .Log Cosh loss:
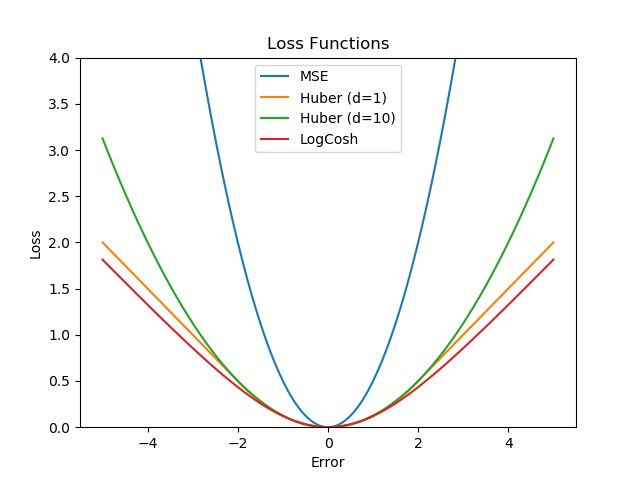
- MSE vs Huber vs Log-Cosh:
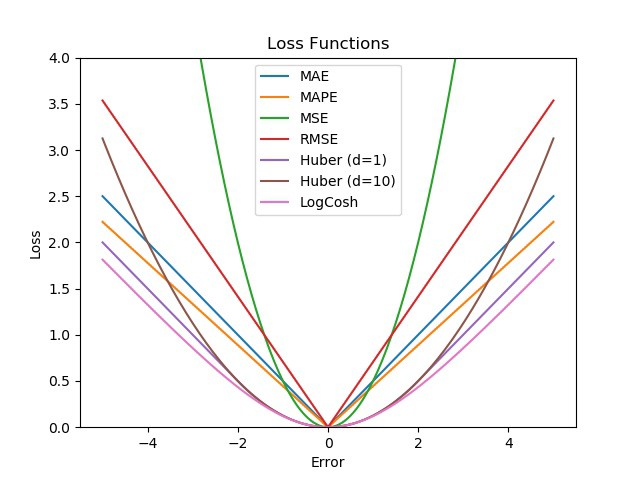
- 损失函数的超级比较:
- Quantile loss">7.分位数损失Quantile loss
- Poisson loss">8.泊松损失Poisson loss
- 9.RMSLE
- 决定系数:R2(R-Square)
- 校正决定系数(Adjusted R-Square)
- Pearson Correlation(皮尔逊相关系数)">Pearson Correlation(皮尔逊相关系数)
- other
1、均方误差:MSE(Mean Squared Error)- L2损失
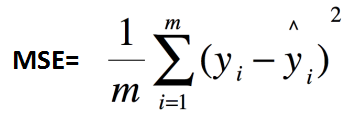
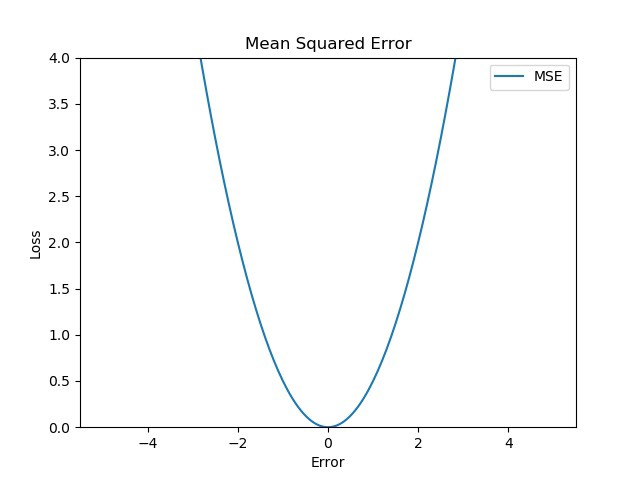
其中,为测试集上真实值-预测值。
在 MSE 中,我们计算误差的平方,然后取其平均值。这是一种二次评分方法,这意味着惩罚不是与误差成正比(如在 MAE 中),而是与误差的平方成正比,这为较大的错误/异常值赋予相对较高的权重(惩罚),同时平滑梯度较小的错误。
优势 :
对于小的误差,MSE 有助于有效地收敛到最小值,因为梯度逐渐减小。
缺点:
对值进行平方确实会提高训练率,但同时,极大的损失可能会导致反向传播期间的急剧跳跃,这是不可取的。
- MSE 对异常值也很敏感,即数据中的异常值可能会更多地影响我们的网络,因为这些异常值的损失会相当高。
2、均方根误差:RMSE(Root Mean Squard Error)
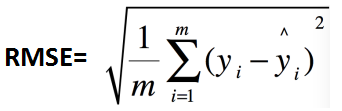
可以看出,RMSE=sqrt(MSE)。
RMSE 只是 MSE 的平方根,这意味着它又是一种线性评分方法,但仍然比 MAE 更好,因为它对较大的错误给予了相对更多的权重。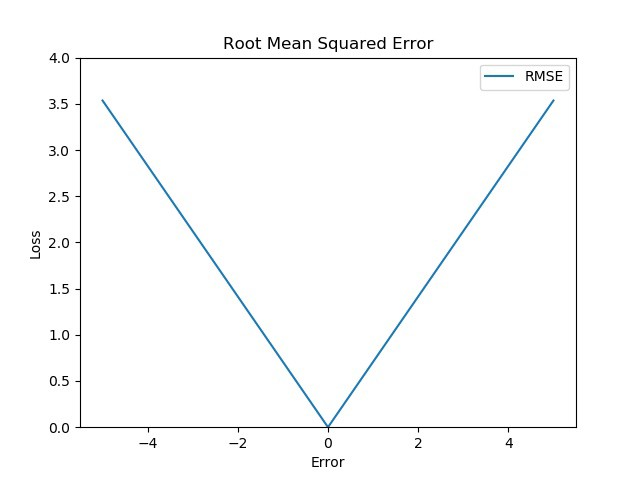
优点 :
3、平均绝对误差:MAE(Mean Absolute Error)
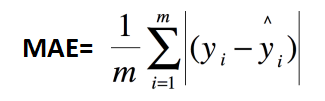
以上各指标,根据不同业务,会有不同的值大小,不具有可读性,因此还可以使用以下方式进行评测。
优点 :
- MAE 是计算损失的最简单方法。
-
缺点 :
MAE 通过考虑相同比例的所有错误来计算损失。例如,如果一个输出是百级的,而另一个是千级的,我们的网络将无法仅基于 MAE 来区分它们,因此,在反向传播期间很难改变权重。
- MAE 是一种线性评分方法,即在计算平均值时对所有误差进行同等加权。这意味着在
反向传播时,由于 MAE 的陡峭性质,我们可能会跳过最小值。
4. MAPE
MAPE 与 MAE 类似,但有一个关键区别,它以百分比计算误差,而不是原始值。因此,MAPE 与我们变量的规模无关。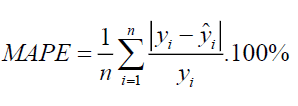

优点 :
损失是通过在一个共同的尺度(一百个)上对所有错误进行归一化来计算的。
缺点:
MAPE 方程在分母中具有预期输出,可以为零。无法计算这些损失,因为没有定义除以零。
- 同样,除法运算意味着即使对于相同的误差,实际值的大小也会导致损失的差异。例如,如果预测值为 70,实际值为 100,则损失为 0.3(30%),而实际值为 40,则损失为 0.75(75%),即使两者都有误差案件是相同的,即30。
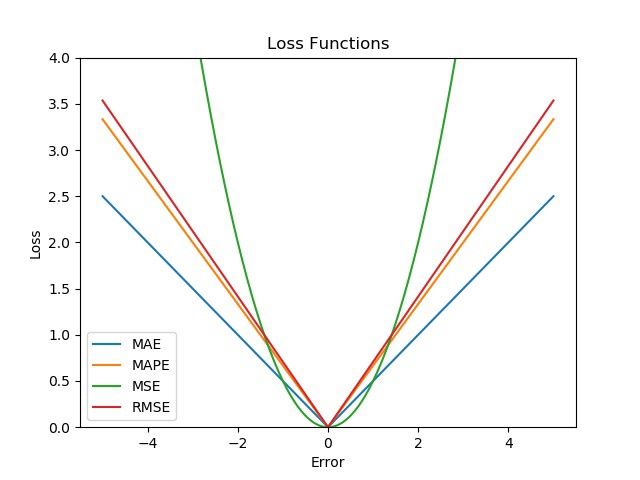
MAE vs MSE vs RMSE vs MAPE:
5. Huber loss -滑平均绝对误差
Huber 损失是线性和二次评分方法的极好组合。它有一个额外的超参数delta (δ)。对于高于 delta 的值和低于 delta 的值,损失是线性的。此参数可根据您的数据进行调整,这使得 Huber 损失变得特别。
数学方程式:
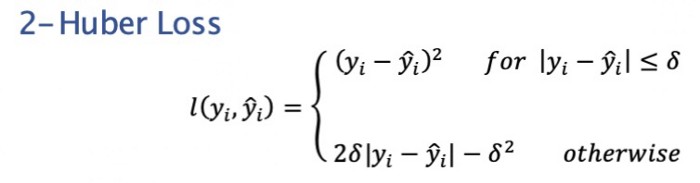
Stack Exchange中的 Huber 损失方程
图:
下图显示了不同 δ 值对误差的 Huber 损失变化。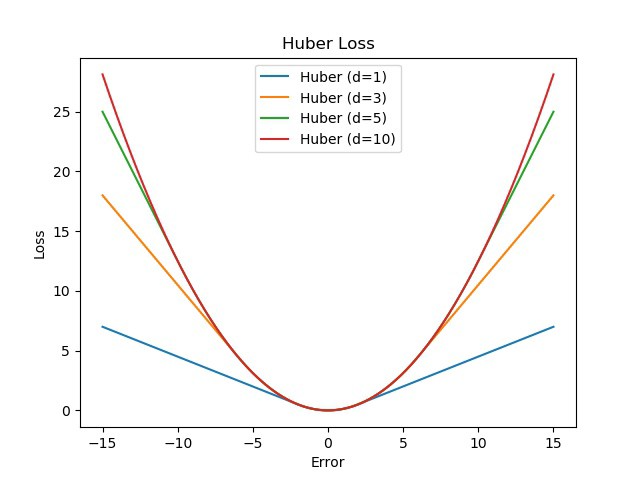
优点 :
- 可修改的超参数增量 (δ)。
- 高于 delta 的线性确保了对异常值的公平权重(不像 MSE 那样极端)。
低于 delta 的曲线特性确保了反向传播期间步长的正确长度。
缺点:
由于额外的条件和比较,Huber 损失在计算方面相对昂贵,尤其是在您的数据集很大的情况下。
- 为了得到最好的结果,δ也需要优化,这就增加了训练要求。
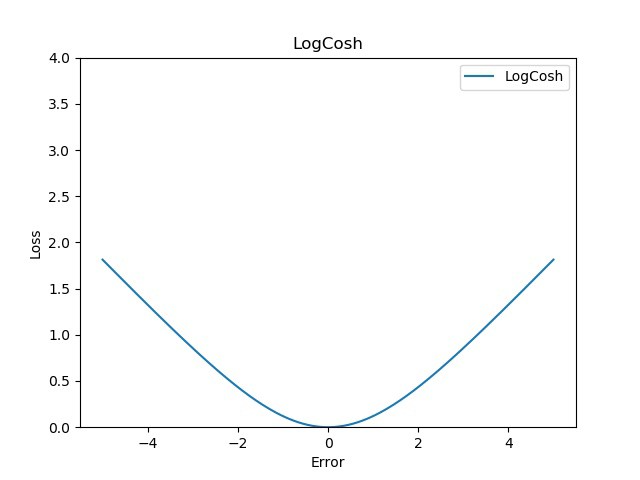
6 .Log Cosh loss:
从图形上看,Log-cosh 与 Huber 损失非常相似,因为它也是线性和二次评分的组合。使其与众不同的一个区别是它是双重可微的。一些优化算法(如 XGBoost) 更喜欢Huber 这样的函数,Huber 只能微分一次。Log-cosh 计算误差的双曲余弦的对数。数学方程式:
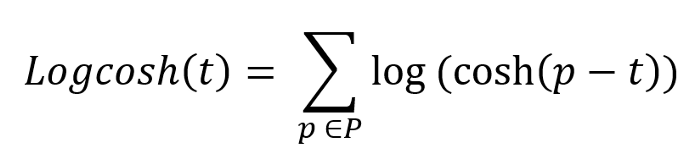
图:
优点 :
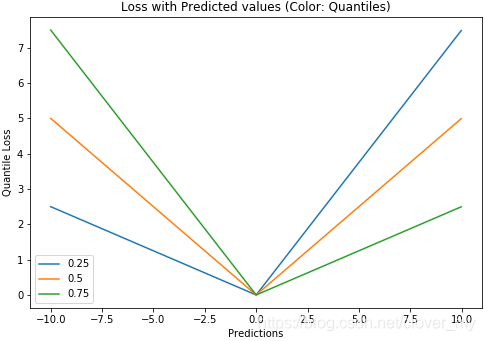
7.分位数损失Quantile loss
8.泊松损失Poisson loss
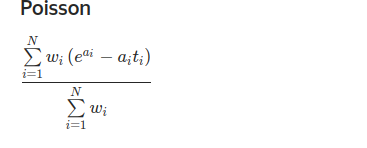
9.RMSLE
1 均方根误差 RMSE(Root Mean Squared Error)
- 均方根对数误差 RMSLE(Root Mean Squared Logarithmic Error)
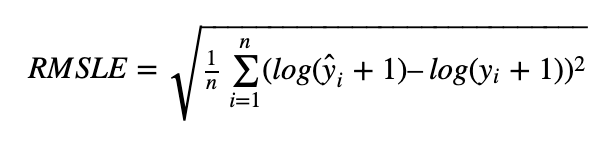
使用 RMSLE 的优点
1.RMSLE 惩罚欠预测大于过预测,适用于某些需要欠预测损失更大的场景,如预测共享单车需求。
假如真实值为 1000,若预测值为 600,那么 RMSE=400, RMSLE=0.510
假如真实值为 1000,若预测值为 1400, 那么 RMSE=400, RMSLE=0.336
可以看出来在 RMSE 相同的情况下,预测值比真实值小这种情况的 RMSLE 比较大,即对于预测值小这种情况惩罚较大。
决定系数:R2(R-Square)
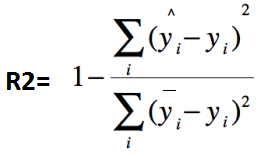
其中,分子部分表示真实值与预测值的平方差之和,类似于均方差 MSE;分母部分表示原始真实值与原始均值的平方差之和,类似于方差 Var。
根据 R-Squared 的取值,来判断模型的好坏,其取值范围为[0,1]:
如果结果是 0,说明模型拟合效果很差;
如果结果是 1,说明模型无错误。
一般来说,R-Squared 越大,表示模型拟合效果越好。R-Squared 反映的是大概有多准,因为,随着样本数量的增加,R-Square必然增加,无法真正定量说明准确程度,只能大概定量。
校正决定系数(Adjusted R-Square)
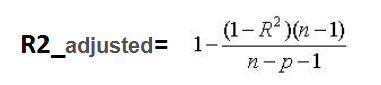
其中,n 是样本数量,p 是特征数量。
Adjusted R-Square 抵消样本数量对 R-Square的影响,做到了真正的 0~1,越大越好。
Pearson Correlation(皮尔逊相关系数)
other
RMSEWithUncertainty
LogLinQuantile
Lq
Expectile
Tweedie
- tweedie, negative log-likelihood for Tweedie regression

FairLoss
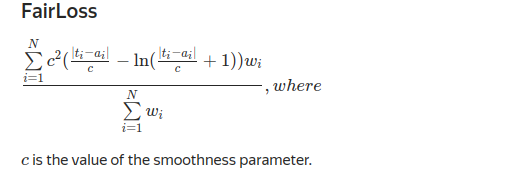
NumErrors
与标签值的差值超过指定值的预测比例 greater_than。SMAPE
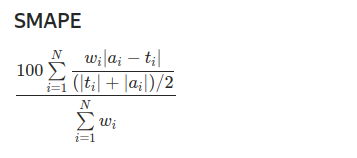
MSLE
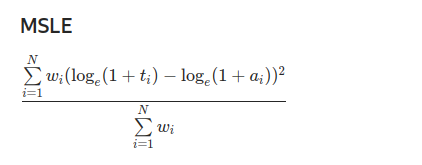
gamma
negative log-likelihood for Gamma regression
- poisson,negative log-likelihood for Poisson regression
- gamma_deviance, residual deviance for Gamma regression
- map, MAP, aliases: mean_average_precision
Regression metrics
| metrics.explained_variance_score(y_true, …) | Explained variance regression score function. | | —- | —- | | metrics.max_error(y_true, y_pred) | The max_error metric calculates the maximum residual error. | | metrics.mean_absolute_error(y_true, y_pred, ) | Mean absolute error regression loss. | | metrics.mean_squared_error(y_true, y_pred, ) | Mean squared error regression loss. | | metrics.mean_squared_log_error(y_true, y_pred, ) | Mean squared logarithmic error regression loss. | | metrics.median_absolute_error(y_true, y_pred, ) | Median absolute error regression loss. | | metrics.mean_absolute_percentage_error(…) | Mean absolute percentage error (MAPE) regression loss. | | metrics.r2_score(y_true, y_pred, [, …]) | R2 (coefficient of determination) regression score function. | | metrics.mean_poisson_deviance(y_true, y_pred, ) | Mean Poisson deviance regression loss. | | metrics.mean_gamma_deviance(y_true, y_pred, ) | Mean Gamma deviance regression loss. | | metrics.mean_tweedie_deviance(y_true, y_pred, ) | Mean Tweedie deviance regression loss. | | metrics.d2_tweedie_score(y_true, y_pred, ) | D^2 regression score function, percentage of Tweedie deviance explained. | | metrics.mean_pinball_loss(y_true, y_pred, ) | Pinball loss for quantile regression. |
https://www.zhihu.com/question/19734616
https://blog.csdn.net/u012735708/article/details/84337262
https://catboost.ai/en/docs/concepts/loss-functions-regression