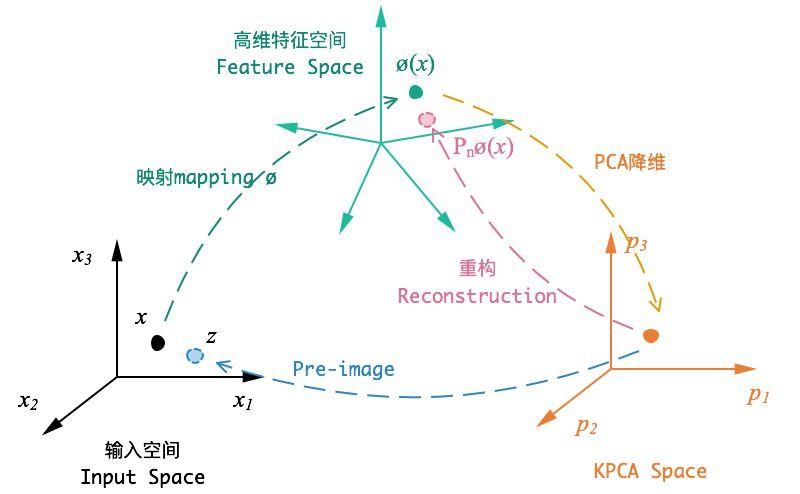
image.png
一般来说，主成分分析(Principal Components Analysis, PCA)适用于数据的线性降维。而核主成分分析(Kernel PCA, KPCA)可实现数据的非线性降维，用于处理线性不可分的数据集。
KPCA的大致思路是：对于输入空间(Input space)中的矩阵 核主成分分析(Kernel PCA, KPCA) - 图2 ，我们先用一个非线性映射把 核主成分分析(Kernel PCA, KPCA) - 图3 中的所有样本映射到一个高维甚至是无穷维的空间(称为特征空间，Feature space)，(使其线性可分)，然后在这个高维空间进行PCA降维。

核主成分分析 (KPCA) 是一种非线性数据处理方法，其核心思想是通过一个非线性映射把原始空间的数据投影到高维特征空间， 然后在高维特征空间中进行基于主成分分析 (PCA) 的数据处理。KPCA通常有以下主要应用：

  • 降维
  • 特征提取
  • 去噪
  • 故障检测

KPCA 建模流程

KPCA 的建模流程如下[1]：

  1. 获取训练数据
  2. 计算核矩阵
  3. 核矩阵中心化
  4. 特征值分解
  5. 特征向量的标准化处理
  6. 主成分个数的选取
  7. 计算非线性主成分
  8. 计算 SPE 和 T2 统计量 （用于故障检测）
  9. 计算 SPE 和 T2 统计量的控制限（用于故障检测）

通过步骤1-7可以实现数据降维或者特征提取（即非线性主成分）。另外，基于 KPCA 的数据重构一般是通过求解近似的逆映射，把所获取的非线性主成分重构到原始空间，本文参考以下资料来实现 KPCA 数据重构实现：

  1. Python 的机器学习库 Scikit-learn (sklearn)：sklearn.decomposition.KernelPCA.inverse_transform

通过步骤1-9实现故障检测模型的建立。对于测试数据，在获取 KPCA 模型的基础上，实现故障检测的流程为：

  1. 获取测试数据
  2. 计算核矩阵
  3. 核矩阵中心化
  4. 计算测试数据的非线性主成分
  5. 计算 SPE 和 T2 统计量（用于故障检测）
  6. 与 SPE 和 T2 统计量的控制限进行比较（用于故障检测）
  7. 若超过控制限，则判断为故障（用于故障检测）

对于步骤7， 通过计算故障区间的 SPE 和 T2 统计量的贡献率来实现故障诊断。本文参考以下资料来实现KPCA故障检测和故障诊断：

  1. Lee J M, Yoo C K, Choi S W, et al. Nonlinear process monitoring using kernel principal component analysis[J]. Chemical engineering science, 2004, 59(1): 223-234. （故障检测）
  2. Deng X, Tian X. A new fault isolation method based on unified contribution plots[C]//Proceedings of the 30th Chinese Control Conference. IEEE, 2011: 4280-4285. （故障诊断）

KPCA

编写了 KPCA 的 代码，主要特点有：

  • 易于使用的 API
  • 基于 KPCA 的数据降维、特征提取、数据重构
  • 基于 KPCA 的故障检测和故障诊断
  • 核函数 ( gaussian, polynomial,, laplacian){‘linear’, ‘poly’, ‘rbf’, ‘sigmoid’, ‘cosine’, ‘precomputed’}
  • 基于主元贡献率或给定数字的降维维度/主元个数选取
  1. # https://github.com/heucoder/dimensionality_reduction_alo_codes/blob/master/codes/PCA/KPCA.py
  2. from sklearn.datasets import load_iris
  3. from sklearn.decomposition import KernelPCA
  4. import numpy as np
  5. import matplotlib.pyplot as plt
  6. from scipy.spatial.distance import pdist, squareform
  8. '''
  9. author: heucoder
  10. email: 812860165@qq.com
  11. date: 2019.6.13
  12. '''
  14. def sigmoid(x, coef = 0.25):
  15.     x = np.dot(x, x.T)
  16.     return np.tanh(coef*x+1)
  18. def linear(x):
  19.     x = np.dot(x, x.T)
  20.     return x
  22. def rbf(x, gamma = 15):
  23.     sq_dists = pdist(x, 'sqeuclidean')
  24.     mat_sq_dists = squareform(sq_dists)
  25.     return np.exp(-gamma*mat_sq_dists)
  27. def kpca(data, n_dims=2, kernel = rbf):
  28.     '''
  29.     :param data: (n_samples, n_features)
  30.     :param n_dims: target n_dims
  31.     :param kernel: kernel functions
  32.     :return: (n_samples, n_dims)
  33.     '''
  34.     # 计算核矩阵
  35.     K = kernel(data)
  36.     #   核矩阵中心化
  37.     N = K.shape[0]
  38.     one_n = np.ones((N, N)) / N
  39.     K = K - one_n.dot(K) - K.dot(one_n) + one_n.dot(K).dot(one_n)
  40.     #    特征值分解
  41.     eig_values, eig_vector = np.linalg.eig(K)
  42.     # 主成分个数的选取
  43.     idx = eig_values.argsort()[::-1]
  44.     eigval = eig_values[idx][:n_dims]
  45.     eigvector = eig_vector[:, idx][:, :n_dims]
  46.     # 特征向量的标准化处理
  47.     print(eigval)
  48.     eigval = eigval**(1/2)
  49.     vi = eigvector/eigval.reshape(-1,n_dims)
  50.     #计算非线性主成分
  51.     data_n = np.dot(K, vi)
  52.     return data_n

结论

在这篇文章中，您大致了解了 KPCA 和非线性降维技术。在实践中，你应该很好地研究你的数据集，以便选择你应该使用什么算法来减少你的维度。另请注意，KPCA 比 PCA 花费更多时间。

https://github.com/JAVI897/Kernel-PCA
https://github.com/heucoder/dimensionality_reduction_alo_codes/blob/master/codes/PCA/KPCA.py
https://zhuanlan.zhihu.com/p/59775730