统计学习方法

第 0 章 说明

0.1 符号表

0.2 参考

[1] https://github.com/SmirkCao/Lihang
[2] http://www.cs.cmu.edu/~tom/mlbook/NBayesLogReg.pdf
[3] http://www.matrix67.com/blog/archives/105
[4] http://www.greenteapress.com/thinkbayes/thinkbayes.pdf
[5] http://cs231n.github.io/linear-classify/

第 1 章 统计学习方法概论

1.1 基础

1.1.1 统计学习

统计学习( statistical learning)是关于计算机基于数据构建概率统计模型并运用模型对数据进行预测与分析的一门学科.统计学习也称为统计机器学习(statistical machine learning)。
统计学习包括监督学习、非监督学习、半监督学习及强化学习。
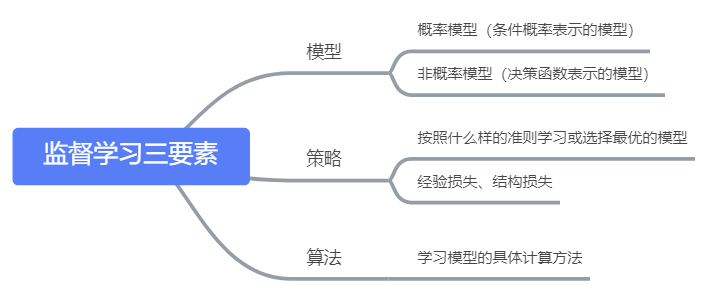
统计学习三要素：模型、策略和算法。

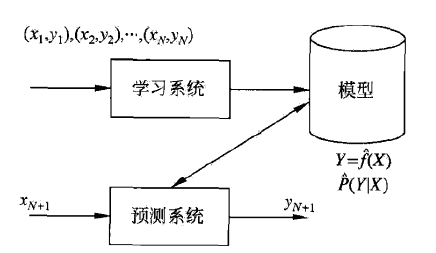
1.1.2 监督学习

任务的分类（根据输入、输出变量的不同类型对预测任务进行分类）：

  - 回归：输入变量与输出变量均为连续变量的预测问题
  - 分类：输出变量为有限个离散变量的预测问题
  - 标注：输入变量与输出变量均为变量序列的预测问题

监督学习分为学习和预测两个过程。

1.1.3 常用损失函数

• 0-1 损失函数

• 平方损失函数

• 绝对损失函数

• 对数损失函数

1.1.4 期望损失、经验损失

期望风险（expected risk）又称为期望损失（expected loss），是模型关于联合分布的期望损失

经验风险（empirical risk）又称为经验损失（empirical loss），是模型关于训练数据集的平均损失

根据大数定律，当样本容量N趋于无穷时，经验风险趋于期望风险。

1.1.5 ERM、SRM

经验风险最小化 (empirical risk minimization. ERM) 结构风险最小化 (structuzal risk minimization. SRM)

• ERM

最大似然估计就是 ERM 的一个例子。

• SRM

结构风险在经验风险上加上表示模型复杂度的正则化项（regularizer）或罚项（penalty term）.

最大后验估计就是 SRM 的一个例子。

1.1.6 训练误差、测试误差

• 训练误差

训练误差是训练的模型关于训练数据集的平均损失

• 测试误差

测试误差是训练的模型关于测试数据集的平均损失

1.1.7 泛化能力

泛化能力（generalization ability）通常指学习方法对未知数据的预测能力。泛化误差反映了学习方法的泛化能力，泛化误差越小，方法越有效。

1.1.8 正则化、交叉验证

_正则化和交叉验证都是两种常用的模型选择方法。

如果给定的样本数据充足，进行模型选择的一种简单方法是随机地将数据集切分成三部分，分别为训练集（training set），验证集（validation set）和测试集（testset）。训练集用来训练模型，验证集用于模型的选择，而测试集用于最终对学习方法的评估。在学习到的不同复杂度的模型中，选择对验证集有最小预测误差的模型。由于验证集有足够多的数据，用它对模型进行选择也是有效的。

• 正则化

正则化是结构风险最小化策略的实现。

• 交叉验证

交叉验证的基本想法是重复地使用数据；把给定的数据进行切分，将切分的数据集组合为训练集与测试集，在此基础上反复地进行训练、测试以及模型选择。
常见的交叉验证方法有：

• 简单交叉验证

随机地将己给数据分为两部分，一部分作为训练集，另一部分作为测试集（e.g. 70%的数据为训练集，30%的数据为测试集）

• S折交叉验证

应用最多的是S折交叉验证（S-fold cross validation）随机地将已给数据切分为S个互不相交的大小相同的子集，后利用S-1个子集的数据训练模型，利用余下的子集测试模型;将这一过程对可能的S种选择重复进行，最后选出S次评测中平均测试误差最小的模型。

• 留p交叉验证

留p交叉验证(leave-p-out crossvalidation）指的是使用全集X中的p个元素作为测试集，然后剩下的n-p个元素作为训练集。根据数学上的定理可以得到，p个元素的选择方法有个。在这个意义下，留p交叉验证的时间复杂度也是非常高的。当p=1的时候，留一交叉验证（Leave-one-out Cross Validation）的复杂度恰好是n。

1.2 拓展

1.2.1 生成式模型、判别式模型

• 生成式模型

生成式模型，主要学习样本的联合概率分布

• Naive Bayes（朴素贝叶斯）
  • 朴素：特征条件独立
• GMM（高斯混合模型）
• Bayesian Network
• MRF（多重参考模型）
  • 判别式模型

判别式模型，主要学习样本的条件概率分布

• Logistic Regression（逻辑回归）
• SVM（支持向量机）
• Neural Network（神经网络）

  1.2.2 大数定理、中心极限定理

• 大数定理

以统计身高为例，一次实验中，随着实验样本数量的不断增加，统计所得的样本的均值就会依概率（弱）或以概率 1 收敛到总体均值。

• 中心极限定理

以统计身高为例，重复多次实验，计算每次实验样本的身高的均值，每次实验的均值都会以总体均值为中心，呈正态分布。

1.2.3 过拟合

• 过拟合产生的原因
  • 假设过于复杂
  • 数据存在很多噪音
  • 数据规模太小
• 如何解决过拟合
  • Early Stopping
    一般的做法是，在迭代过程中，记录到目前为止最好的验证精度，如果连续十代没有提升精度，那么就认为精度不会再提高，此时便可以停止迭代。
  • 数据集扩增
    调整已有的数据，添加大量的“噪音”，或者对图像进行锐化、旋转、明暗度调整等优化。
  • 正则化在目标函数的 Cost Function 后面加上正则项。
    • L1 正则化
    • L2 正则化
  • Dropout
  • 换个模型
    对于模型的设计，目前公认的一个深度学习规律“deeper is better”。国内外各种大牛通过实验和竞赛发现，对于CNN来说，层数越多效果越好，但是也更容易产生过拟合，并且计算所耗费的时间也越长。因此对于模型的设计需要合理参考各种模型的取舍。
  • 可变化的学习率
    一个简单的方法是在人为设定的准确率范围内，达到10次范围内的波动后，依次将学习率减半，直到最终的学习率降为原始的 1/1024 时停止模型的训练。
  • BN
    据在经过卷积层之后，真正进入激活函数之前需要对其进行一次 Batch_Normalization，分批对输入的数据求取均值和方差之后重新对数据进行归一化计算。对数据进行预处理，对数据点中的误差进行掩盖，增大模型的泛化能力

1.3 总结

1.3.1 监督学习三要素

第 2 章 感知机

2.1 基础

2.1.1 感知机模型

感知机（perceptron） S（separating hyperplane）

感知是一个二分类模型，其通过定义一个超平面S，将特征空间分为两个部分。超平面定义为

其中w（weight）称为权值，是超平面的法向量，b（bias）称为偏置。通过训练数据来学习w和b。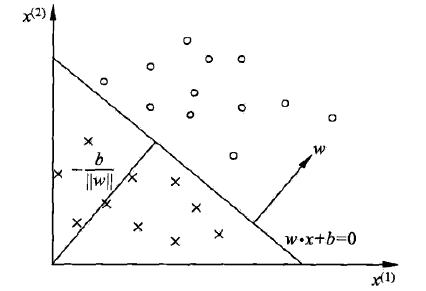

2.1.2 感知机策略

M: 超平面S的误分类点的集合

损失函数定义为误分类点到超平面S的总距离。（为什么不使用误分类点的个数作为损失函数？因为这样的损失函数不是参数w,b的连续可导函数，不可优化。）
W中所有元素到超平面S的距离为

其中是w的范数。
不考虑分子，定义感知机的损失函数（经验损失）为

2.1.3 感知机算法的原始形式

感知机学习算法是误分类驱动的，具体采用SGD（stochastic gradient descent）。

当一个实例点被误分类后，通过更新w（法向量）改变超平面的方向，通过更新b（偏置）来移动超平面。
Gradient：

Update：

2.1.4 感知机算法的对偶形式

对偶形式的基本思想是将w和b表示为实例和标记的线性组合的形式，通过求解其系数而求得w和b。

输入：

输出：

1. 初始化
2. 训练集中选取数据
3. 如果

1. 转至(2)，直至训练集中没有误分类点

   2.2 拓展

   2.2.1 矩阵范数

   参考链接：wiki

2.2.2 对偶形式

参考链接：知乎

对偶形式里面包含一个预先存储的矩阵Gram矩阵（Gram matrix），相对于之前的原始形式，在更新的时候，只要索引矩阵的元素就可以了，无需每次都重复计算。

2.3 总结

2.4 疑问

2.4.1 算法2.1（感知机学习算法的原始形式）

第 3 章 k 近邻法

3.1 基础

3.1.1 k近邻法

k近邻法（k-nearest neighbor，k-NN）

kNN是一种基本分类与回归方法。训练后的模型，在训练数据集中找到输入最邻近的k个实例，这k个实例的多数属于某个类，就把该输入分为这个类。
当k=1时，称为最近邻算法，将训练集中与x最邻近的点的类作为输入的类。

3.1.2 模型

特征空间中，对每个训练实例点，距离该点比其他点更近的所有点组成一个区域，叫作单元（cell），每一个cell中的所有点都属于类（label class），所有训练实例点的单元构成对特征空间的一个划分。
e.g.（二维特征空间）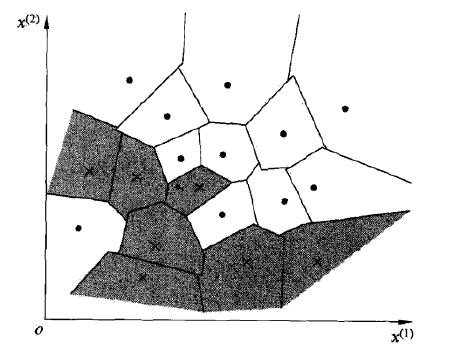

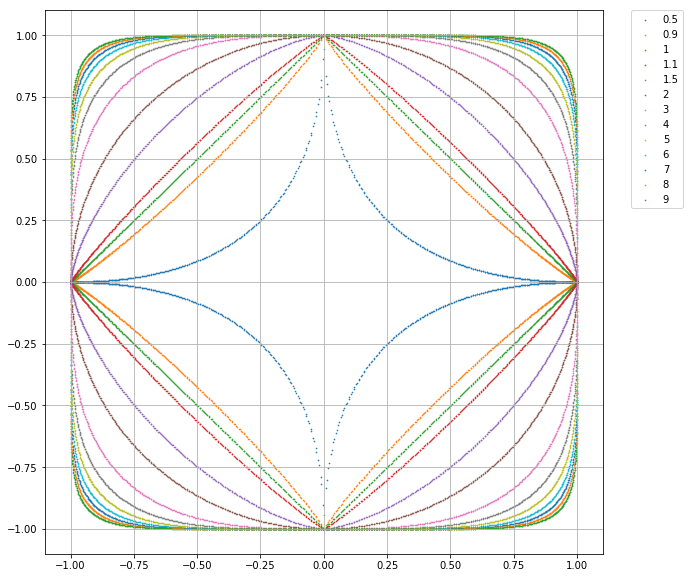
3.1.3 距离度量

特征空间中两个实例点的距离反映了两个实例点的相似程度，一般使用距离。

两个点的距离定义为

• 当时，称为曼哈顿距离（Manhattan distance）
• 当时，称为欧式距离（Euclidean distance）
• 当时，它是各个坐标距离的最大值（）

二维空间中的示例（不同p值下，与原点距离相同的点的集合）

3.1.4 k值的选择

k值越大，模型越简单，但预测的错误几率就越大；k值越小，模型越复杂，但也容易发生过拟合。在应用中，k值一般取一个比较小的数值.通常采用交叉验证法来选取最优的k值。

3.1.5 分类决策规则

多数表决规则（majority voting role），如果分类损失规则采用0-1损失函数

误分类率是

多数表决规则目的是为了使误分类率最小，即最小，即经验损失最小。

3.1.5 kd树

k近邻法最简单的实现方法是线性扫描（linear scan）。这时要计算输入实例与每一个训练实例的距离。当训练集很大时，计算非常耗时，这种方法是不可行的。
kd树是二叉树，表示对k维空间的一个划分（partition）。构造kd树相当于不断地用垂直于坐标轴的超平面将k维空间切分，构成一系列的k维超矩形区域。kd树的每个结点对应于一个k维超矩形区域。
构造（平衡）kd树的算法：

• 初始：以为坐标轴，计算所有实例在上的投影的中位数，用与垂直的超平面将根节点的超矩形区域划分为两个子区域。
• 重复：，对深度为j的节点，以为坐标轴，重复初始步骤。

e.g. 二维特征空间的划分

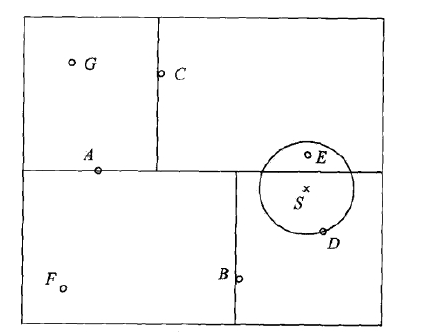
3.1.6 kd树的搜索

A是根节点，S是待分类的点，先在区域内找到D，以D作为近似最近邻开始寻找。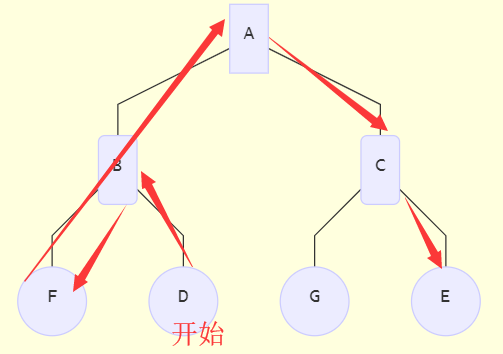

3.2 拓展

3.3 总结

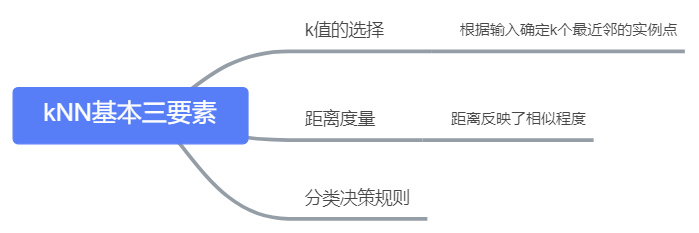
3.3.1 kNN的基本三要素

第 4 章 朴素贝叶斯

4.1 基础

4.1.1 朴素贝叶斯

朴素贝叶斯（naive Bayes）法是基于贝叶斯定理与特征条件独立假设的分类方法，属于生成式模型。

4.1.2 拉普拉斯平滑

拉普拉斯平滑（Laplace smoothing）

为了防止实际中出现某些在训练集中未出现过的特征（所要估计的概率分子分母均为0），贝叶斯估计的分子分母加上修正项。
修正后的条件概率

其中表示第个特征可能取的第个值，
修正后的先验概率

其中表示第个类，
一般正数取1，当，条件概率就是MLE。

4.2 拓展

4.2.1 贝叶斯准则

贝叶斯准则为

• ，先验概率
• ，归一化比例因子
• ，后验概率
• ，似然估计

  4.2.2 Naive Bayes与Logistic Regression的区别

  NBayesLogReg.pdf

4.3 总结

第 5 章 决策树

5.1 基础

5.1.1 决策树模型

决策树（decision tree）

分类决策树模型是一种描述对实例进行分类的树形结构。决策树由有向边（directed edge）和节点（node）组成。结点有两种类型:：内部结点（internal node）和叶结点（leaf node）。内部结点表示一个特征或属性，叶结点表示一个类。<br />如下图所示，其中圆形表示一个内部节点（特征），方形表示叶节点（类）。

在决策树算法中，寻找最优决策树是一个NP-complete问题。决策树的这一特点，说明我们无法利用计算机在多项式时间内，找出全局最优解。

5.1.2 算法——特征选择

特征选择在于选取对训练数据具有分类能力的特征，通常特征选择的准则是信息增益或信息增益比。

• 信息增益

信息增益（information gain）表示得知特征X的信息而使得类Y的信息的不确定性减少的程度，即采用X特征使训练集的熵减小的程度。
特征A对训练数据集D的信息增益g(D,A)，定义为集合D的经验熵H(D)与特征A给定条件下D的经验条件熵H(D|A)之差，即

一般的，熵和熵的差成为互信息（mutual information）

• 信息增益比

信息增益比定义为

5.1.3 算法——决策树的生成

ID3和C4.5是决策树生成的两个经典的算法。

• ID3算法

ID3算法从根节点开始，计算所有可能的特征的信息增益（information gainsd），选取最大的特征作为该节点的特征，由该特征的不同值建立子节点。再对子节点进行同样操作，知道所有特征的信息增益均很小或没有特征选择为止，最终得到一个决策树。
ID3算法只有树的生成，所以该算法生成的树容易产生过拟合。

• C4.5算法

C4.5算法与ID3算法相似，不同的是：C4.5在生成的过程中，用信息增益比来选择特征。

5.1.4 算法——决策树的剪枝

决策树的剪枝（pruning）是指为了减小决策树的复杂度，防止过拟合的出现，从已生成的树上裁掉一些字数或者叶节点的过程。
决策树学习的损失函数可以定义为

其中树T的叶结点个数为|T|，t是树T的叶结点，该结点有个样本点，其中k类的样本点有个，为叶结点t上的经验熵， 为参数。
并且

这时有

其中表示模型对训练数据的误差，|T|表示模型复杂度，参数进行加权，控制两者之间的影响比重。
关键思想：
在每个叶节点上尝试回缩，如果回缩过后的损失函数的值较小，那么就把这个叶节点裁去。

5.1.5 CART算法

• 特征选择：基尼指数（Gini index）最小化准则

CART算法在进行决策树的生成时，比较的是基尼指数。
概率分布的基尼指数定义为

• 决策树的剪枝

CART剪枝算法由两步组成：首先从生成算法产生的决策树底端开始不断剪枝，直到的根结点，形成一个子树序列；然后通过交叉验证法在独立的验证数据集上对子树序列进行测试，从中选择最优子树.

5.2 拓展

5.2.1 时间复杂度

O(1)：常数级复杂度 O(n)：线性时间复杂度 O(log n)：对数时间复杂度 O(P(n))：多项式时间复杂度（e.g. ）

时间复杂度用来描述一个算法的运行时间，但并不是表示一个算法解决问题需要花多少时间，而是当问题规模扩大后，程序需要的时间长度增长得有多快。

5.2.2 约化

约化（reducibility，归约）

在可计算性理论与计算复杂性理论中，所谓的归约是将某个计算问题转换为另一个问题的过程。简单点来说，一个问题A可以约化（归约）为问题B的含义即是可以用问题B的解法解决问题A。
「问题A可约化为问题B」有一个重要的直观意义：B的时间复杂度高于或者等于A的时间复杂度。
e.g. 一元一次方程和一元二次方程
求解一个一元一次方程的问题（A）可以归约为求解一个一元二次方程。

5.2.2 P、NP、NP-H、NP-C问题

P（polynomial） NP（nondeterministic polynomial） NP-H（NP-hard） NP-C（NP-complete ）

上面的时间复杂度和归约都是为了这个问题服务。
首先，这几个问题的包含所属关系如下图所示。所有P问题都是NP问题，反之则不一定。NP-complete问题是NP问题的子集。如果找到一个多项式内能被解决的NP-complete问题的解决方法，那么P=NP。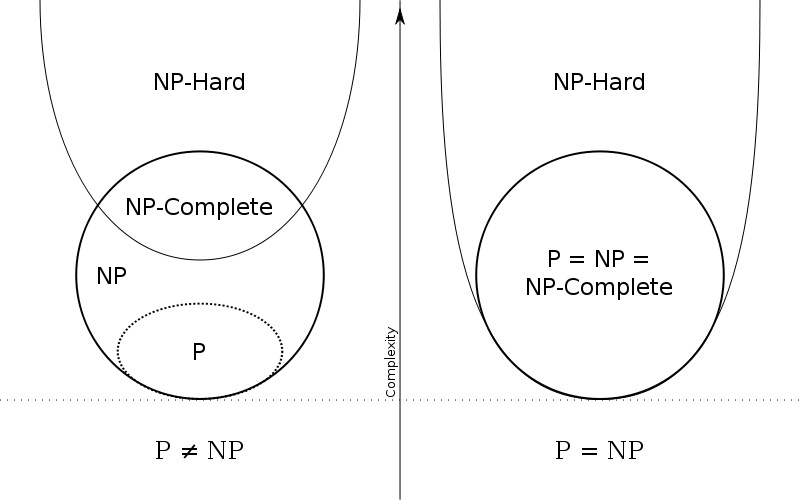

其次，解释各个问题的具体定义。

• P 问题

如果一个问题可以找到一个能在多项式的时间里解决它的算法，那么这个问题就属于P问题。

• NP 问题

NP问题是指可以在多项式的时间里验证（猜出）一个解的问题。
NP问题不是非P类问题，之所以要定义NP问题，是因为通常只有NP问题才可能找到多项式的算法。

• NP-complex 问题

NP-C的定义是：

• 是一个NP问题
• 所有的NP问题都可以归约到这个问题

即存在这样一个NP问题，所有的NP问题都可以约化成它。换句话说，只要解决了这个问题，那么所有的NP问题都解决了。

• NP-hard 问题

NP-hard问题只需要满足NP-complete问题的第二点，即存在一个问题，所有的NP问题都可以归约到这个问题。

5.3 总结

第 6 章 Logistic Regression 和最大熵模型

6.1 基础

6.1.1 LR （模型）

二阶LR模型（binomial logistic regression model）

Logistic Distribution 的数学表达为：

其中，当表达式中的时，其就变成了常见的激活函数Sigmoid。
二项LR模型定义为如下的条件概率分布：

若是将bias加到weight上，并给x增加一个元素1，则可以将变成
在这里引入 6.2.1 中的几率（odds），再取个对数（log odds），此时就可以将概率分布映射到输入的线性组合上，即可以通过训练参数，对输入实体（的特征）进行线性组合，得到事件发生的条件概率。
几率：

对数几率：

对于二项LR模型，有：

对于多项LR模型（multi-nominal logistic regression model），有：

6.1.2 参数估计（算法）

在得到二项LR模型之后，唯一需要确定的就是参数，一般应用MLE（极大似然估计）估计模型参数。
这里，为了书写简洁，定义

采用对数似然函数，有：

即：

需要注意的是，上面的前提是二项LR模型，当多项分类目标时，可以采用指数似然函数

6.1.3 最大熵

6.2 拓展

6.2.1 几率

几率（odds）

在我们想要去表示一件事情发生的可能性时，一般会采用一个0-1的数（概率）。除此之外，为了更好的表示某些事件，类似于比赛谁赢谁输，AB之间选择时，我们可以采用一种新的表示方法：几率（odds），简单来说，就是一件事情发生的概率与它不发生的概率的比值。当然，除此之外，结合贝叶斯公式（“Think Bayes”Chapter 5）即某些应用（LR）来看，几率可能是一个更好的方法。
几率（odds）定义为：

值得注意的是，当几率和贝叶斯定理结合在一起时，可以帮助我们节省一些不必要的步骤（如evidence的计算）。
对于bayes公式：

若有，则有：

若我们只关注D情况下P(A)和P(B)的大小，如上式，显然几率的作用更大一些，并且省去了计算P(D)。
thinkbayes.pdf

6.2.2 各类熵

6.2.3 基于MCC的可变步长自适应滤波器

下面的PPT是自适应课程所做的论文阅读报告。
基于MCC的可变步长自适应滤波器.pdf

6.3 总结

第 7 章 SVM

7.1 基础

7.1.1 函数间隔、几何间隔

函数间隔（functional margin） 几何间隔（geometric margin）

• 函数间隔

对于给定数据集和超平面，定义超平面关于样本点的函数间隔为

定义超平面关于训练数据集的函数间隔为超平面关于中所有样本点的函数间隔之最小值，即

函数间隔可以表示分类预测的正确性及确信度。

• 几何间隔

参考函数间隔，集合间隔定义为

其中是的二范数。
同样的，定义最小几何间隔为

函数间隔和几何间隔的者的数学关系如下所示

• 总结

超平面的参数w（weight）可以看作是超平面的法向量，一个实例与超平面的函数间隔相当于是其与法向量w的内积，而几何间隔就相当于是实例在法向量上的投影。之所以会有，是因为可以决定这个实例是在超平面所划分的正负空间的哪一部分（也可以说是在超平面上面还是下面）。

7.1.2 硬间隔、软间隔

7.1.3 线性可分 SVM

线性可分 SVM（linear support vector machine in linearly separable case）

线性可分SVM的模型的思想和感知机一样，都是找到一个超平面将特征空间中的实例区分开来，但线性可分SVM主要是通过硬间隔最大化构造一个约束最优化问题，通过求解这个问题得到唯一确定的超平面，此超平面不仅将正负实例分割开来，同时将最难分的实例点，即与超平面几何间隔最小的点以最大的确信度进行区分。（why not 函数间隔？猜测是因为防止在训练时为了使距离很小从而使得w和b变得很小）
约束最优化问题为

因为在优化过程中当我们找到距离超平面最近的点时，可调的参数就只有w和b，因此

• 最大化支持向量和超平面的几何间隔
• 最大化支持向量在法向量上面的投影
• 固定函数间隔，最大化，即最小化

这几个方法是等价的，所以上面的最优化问题（第1个）可以等价于下面的最优化问题（第3个，设函数间隔为1），需要注意的是，等价于

这就是线性可分SVM的算法，通过解这个问题我们可得到线性可分SVM的超平面。因此我们的决策函数为。

7.1.4 线性 SVM

线性 SVM（linear SVM）

当遇到线性不可分的数据集时，即某些特例点（outlier）不能满足不等式，线性可分SVM就不再适用。
要是还想应用SVM去解决，可以给每一个样本点都增加一个松弛变量，这样不等式变为，同样的，损失函数变为（前半部分代表间隔最大，后半部分代表减小误分类点的个数）。

7.1.5 非线性SVM

非线性 SVM（non-linear SVM）

7.1.6 对偶问题

这里的SVM的对偶思想与之前感知机的对偶思想是一样的，都是为了减少实际计算中的复杂度，提前计算储存一个Gram矩阵，用一个参数的更新代替参数的更新。为什么可以这样做的原因是因为通过数学推导，分别对w和b求导并令其等于0可以将w表示成x和y的函数，代入原函数可以得到的形式。

7.2 拓展

7.2.1 凸二次规划

凸二次规划（convex quadratic programming）

7.2.2 SVM versus Perceptron

• 不同点
  • Perceptron（感知机）通过不断输入训练集，从而调整超平面，使得超平面可以将正负实例分割开来。因此若输入的训练集顺序重排（主要是初值？），最终得到的超平面就有可能发生变化，这也表明了满足Perceptron的超平面不是唯一的。
  • SVM（支持向量机）通过最靠近超平面的点（支持向量）的距离构造了一个约束最优化问题，通过训练集来求解最优化问题，这样得到的超平面是唯一的，其满足间隔最大化。
  • 如下图所示，从loss function来看，Perceptron只要分类正确，损失就是0，而SVM不但要求分类正确，还要求确信度高，此时损失函数才能是0。

7.2.3 SVM versus Softmax

参考了 CS231n 的 note

下面是SVM分类器和Softmax分类器对一个实例的处理过程的对比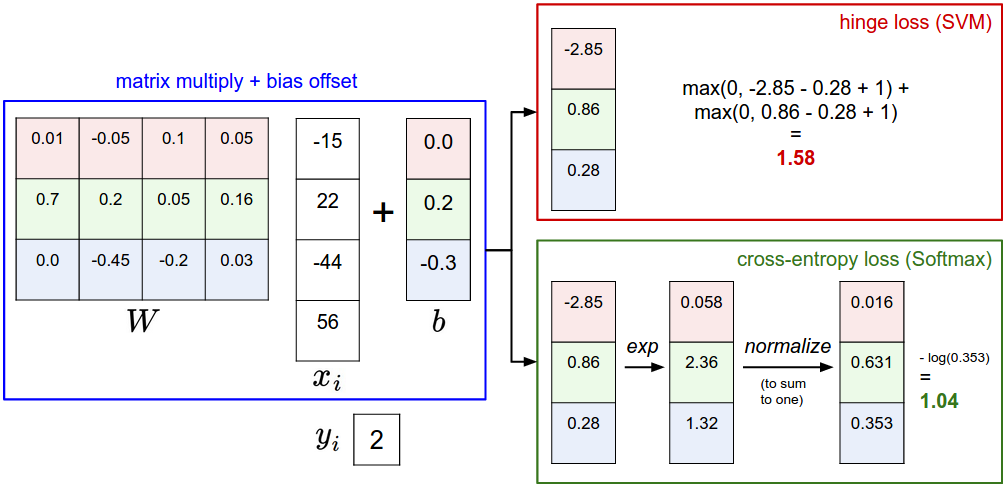

7.2.3 对 bias 的理解

SVM中超平面的b（bias）相当于是给超平面增加了自由度（如二维空间中如果没有b，即，则此时超平面必须经过原点，这样超平面可适应的情况就少了），神经网络中的b可以看作是一个阈值（如采用Relu激活函数，若无b，0是确定的分界线；若有b，可以通过训练找到一个更好的阈值）或者是对分别对各个类别的偏置。

7.2.4 Hard or Soft margins

参考Stack Overflow中的第一个回答

7.3 总结

7.3.1 SVM

7.3.2 Loss

几种方法（0-1，SVM，Softmax，Perceptron）的Loss如下图所示。
其中，Softmax取了六个点设置为六个类（-1，-0.5，0，0.5，1，1.5）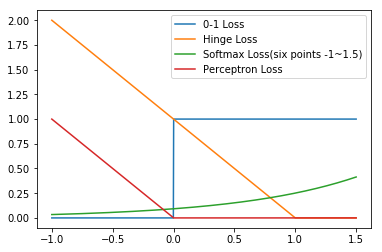

第 8 章 提升方法

书中主要介绍的提升（Boosting）方法为 AdaBoost

8.1 基础

8.1.1 Boosting

PAC：概率近似正确（probably approximately correct，PAC）

因为 Schapire 证明了强可学习方法和若可学习方法是等价的，即互为充要条件。因此，当我们找到了一个弱可学习算法，就可以将他提升（Boost）为强可学习算法。
具体的，对于分类问题，我们可以将很多粗糙的弱分类器组合成为一个强分类器。在这个过程中，我们需要解决两个问题：

• 训练集大小是一定的，我们如何才能得到很多不同的弱分类器

AdaBoost 提高那些被前一轮弱分类器错误分类样本的权值而降低那些被正确分类样本的权值，这样一来，那些没有得到正确分类的数据由于其权值的加大而受到后一轮的弱分类器的更大关注。

• 如何将这些弱分类器合并成为一个强分类器

AdaBoost采取加权多数表决的方法，即加大（减小）分类误差率小（大）的弱分类器的权值，使其在表决中起较大（小）的作用。

8.1.2 AdaBoost 算法

AdaBoost 最终得到的分类器如下所示

其中

  - ![](https://cdn.nlark.com/yuque/__latex/5d09697085e8b2d48446837da84789a3.svg#card=math&code=G%28x%29&height=24&width=34)：最终得到的强分类器
  - ![](https://cdn.nlark.com/yuque/__latex/edeb5520c7164b5f94eb2c06a833f9a4.svg#card=math&code=G_m%28x%29&height=24&width=46)：第 m 个弱分类器
  - ![](https://cdn.nlark.com/yuque/__latex/9fdca6a007df796b924aa43bd2937fdc.svg#card=math&code=%5Calpha_m&height=24&width=22)：第 m 个弱分类器在组合成![](https://cdn.nlark.com/yuque/__latex/dc021d92950d56c8d3447705c258d4fa.svg#card=math&code=G%28m%29&height=24&width=40)时所占的比重

具体的更新过程为

• 初始化（）

初始化第一个分类器中各个训练实体的权值，得到训练数据的初始权值分布（均匀分布）：

由改训练数据训练得到第一个弱分类器。

• 迭代（ ）

通过第m个弱分类器，得到输出结果，计算该分类器的分类错误率

由错误率得到该分类器在最终的强分类器中的系数

由计算得到的系数以及所对应的的训练数据的权值分布来更新新的权值系数从而得到

• 最终结果

值得注意的是，随着不断更新迭代，似乎错误率会一直下降，但实际上存在一个误差下界，随着不断迭代，错误率曲线会无限逼近错误下界。
AdaBoost 算法最终分类器的训练误差界定义为

同时，下面的这个推论证明了AdaBoost的训练误差是以指数速率下降的。
如果存在，对所有 有，则

8.1.3 AdaBoost 的解释

可以认为 AdaBoost 算法是模型为加法模型，损失函数为指数函数，学习算法为前向分步算法的二分类学习方法。
加法模型（additive model）

基本学习算法

前向分步算法
前向分步算法的思想与前文的 AdaBoost 学习算法基本一致，都是从一个基函数（弱分类器）开始，在每一步优化如下损失函数得到基函数参数，随着不断输入基函数，每一步得到的模型都是之前的输入的基函数的加权得到，这样不断更新，直到用完所有的基函数并得到最终的模型。

具体步骤

• 初始化
• 对
• 极小化损失函数
  

• 更新

• 得到加法模型

AdaBoost 算法
用加法模型来解释AdaBoost，每一个基函数对应的就是学习加权后输入数据得到的弱分类器，采用的损失函数是指数函数。

8.1.4 提升树

提升树（Boosting Tree）

以决策树为基函数的提升方法称为提升树。提升树模型如下所示，其中表示决策树，为决策树的参数，M 为树的个数。

当采用平方损失函数来解决回归问题时，具体步骤为

• 初始化

• 对

  1. 计算残差

     

  2. 拟合残差学习一个回归树，得到

  3. 更新

  

• 得到回归问题提升树

8.1.5 梯度提升

梯度提升（gradient boosting）

梯度提升方法主要体现在对残差的处理中，是为了处理不易优化的损失函数。相对于上面的平方损失函数，梯度提升方法在得到每一步的回归树之后会在回归树的叶节点区域搜索可以使损失函数最小化的值，以此来更新回归树。
具体的步骤为

• 初始化

• 
  • 对，计算

  - 对![](https://cdn.nlark.com/yuque/__latex/7657683495075760cd15e2f50f2de376.svg#card=math&code=r_%7Bmi%7D&height=24&width=23)拟合一个回归树，得到第m棵树的叶节点区域![](https://cdn.nlark.com/yuque/__latex/e59665ac17b41ebce527d2532314e8a3.svg#card=math&code=R_%7Bmj%7D%2C%20j%3D1%2C2%2C%5Cdots%2CJ&height=25&width=134)
  - 对![](https://cdn.nlark.com/yuque/__latex/6773309b7de73049b480d52cb6aa5394.svg#card=math&code=j%3D1%2C2%2C%5Cdots%2CJ&height=24&width=98)，计算

  - 更新<br />

• 得到回归树
  

8.2 拓展

8.2.1 SRN-Deblur

SRN-Deblur貌似就是采用的这种思想，不过那里训练的网络就是一个网络，即只训练一个基函数，并不进行加权。其通过对输入数据进行不同速率的下采样得到不同输入数据，并把前一组的输出和本组图片进行组合作为本组模型的输入。

8.2.2 常见分类和回归损失函数

参考知乎一回答

需要思考的问题是：损失函数的不同是否决定了你要解决的问题种类的不同（回归 or 分类）？

8.3 总结

8.3.1 AdaBoost 算法

尝试从加法模型的角度去理解 AdaBoost 函数的错误率下界，当给定的训练集一定时，从这个训练集得到的经过系数加权的训练集不可能每个都是完全不同的，换言之，这些衍生出来的数据集不是正交的，因此尽管加权得到的训练集的数目可能无穷多，但是数量的增多只能让模型尽可能多学会原输入特征空间的特征，并不会产生新的特征，所以最终一定会到达一个极限。这个极限，就是错误率下界存在的原因。

第 9 章 EM 算法及推广

9.1 基础

9.1.1 EM 算法

EM 算法：期望极大算法（Expectation Maximizationg algorithm） 观测变量（observable variable） 潜在变量（latent variable）

EM 算法就是含有隐变量的概率模型参数的极大似然估计或极大后验估计。

形象理解EM算法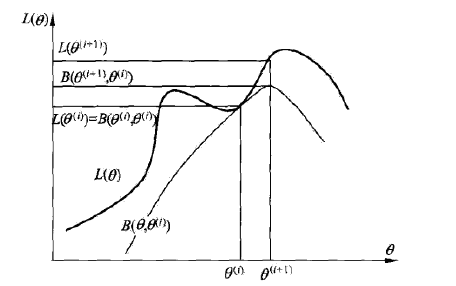

从图中我们不难发现，ＥＭ算法容易陷入局部最优解．

9.1.2 收敛性

• 定理 1

• 定理 2

设为观测数据的对数似然函数，为EM算法得到的参数估计序列，为对应的对数似然函数序列。
（1）如果有上界，则收敛到某一值；
（2）在函数与满足一定条件下，由 EM 算法得到的参数估计序列的收敛值是的稳定点。

9.1.3 高斯混合模型

高斯混合模型（Gaussian misture model）

高斯混合模型定义为如下形式的概率分布模型

很容易理解，是第k个分（高斯）模型的参数，表示的是在总共K个分模型中第k个分模型出现的概率，所以自然会有。其中。
高斯混合模型的EM算法，具体步骤如下

• 确定模型参数初始值并开始迭代
• E 步：依据当前模型参数，计算分模型 k 对观测数据 的响应度

• M 步：计算新一轮迭代的模型参数

• 重复 E 步和 M 步，直到收敛。

  9.1.4 EM 算法的推广

  GEM：广义EM算法（Generalized Expectation maximization）

9.2 拓展

9.2.1 Gradient

参考：wiki-梯度（Gradient）

• 对向量的梯度
  • 以n×1实向量x为变元的实标量函数f(x)相对于x的梯度为一n×1列向量x，定义为

• m维行向量函数相对于n维实向量x的梯度为一n×m矩阵，定义为

• 对矩阵的梯度
  • 实标量函数相对于m×n实矩阵A的梯度为一m×n矩阵，简称梯度矩阵，定义为

9.3 总结

第 10 章 隐马尔科夫模型

10.1 基础

10.2 拓展

10.3 总结