【Matlab】

[toc]

A 特殊矩阵

A.a 通用性矩阵

以上函数调用格式相同，以zeros为例：

例题：

A.b 用于专门学科的特殊矩阵

例题：

rat:有理数

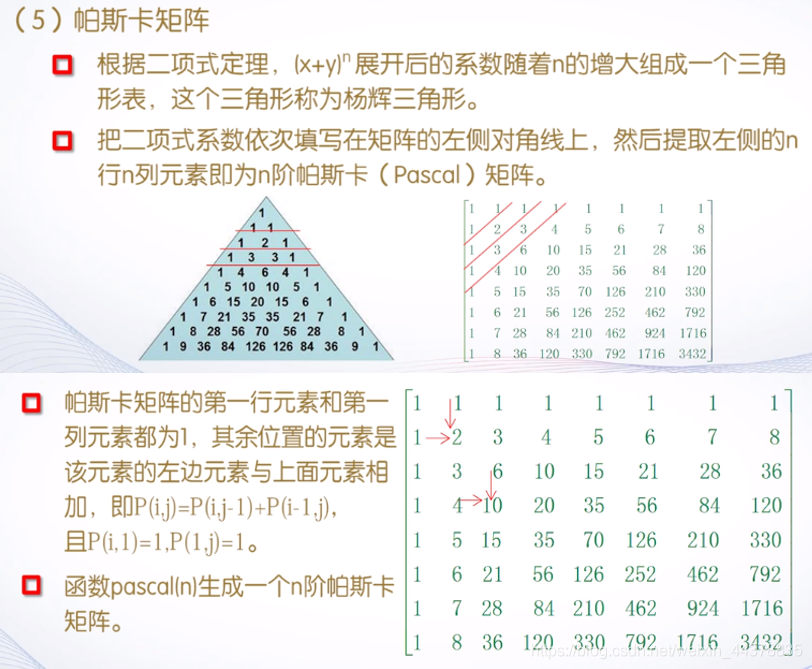
例子：

B 矩阵变换

B.a 对角阵

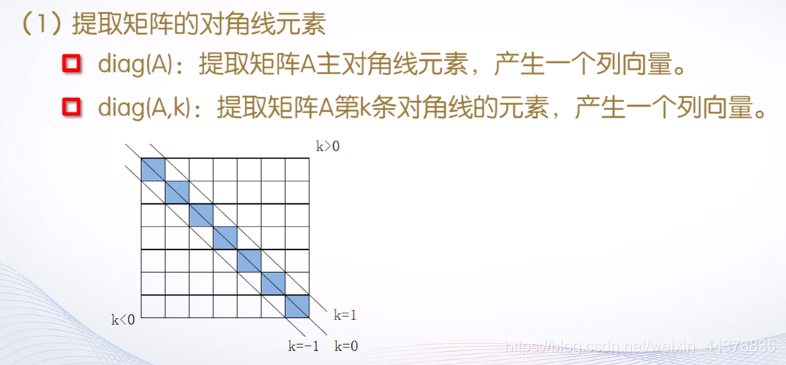
例题：

B.b 三角阵

B.c 矩阵的转置

例子：

B.d 矩阵的旋转

B.e 矩阵的翻转

B.f 矩阵的求逆

例题：

C 矩阵求值

C.a 矩阵的行列式

例题：

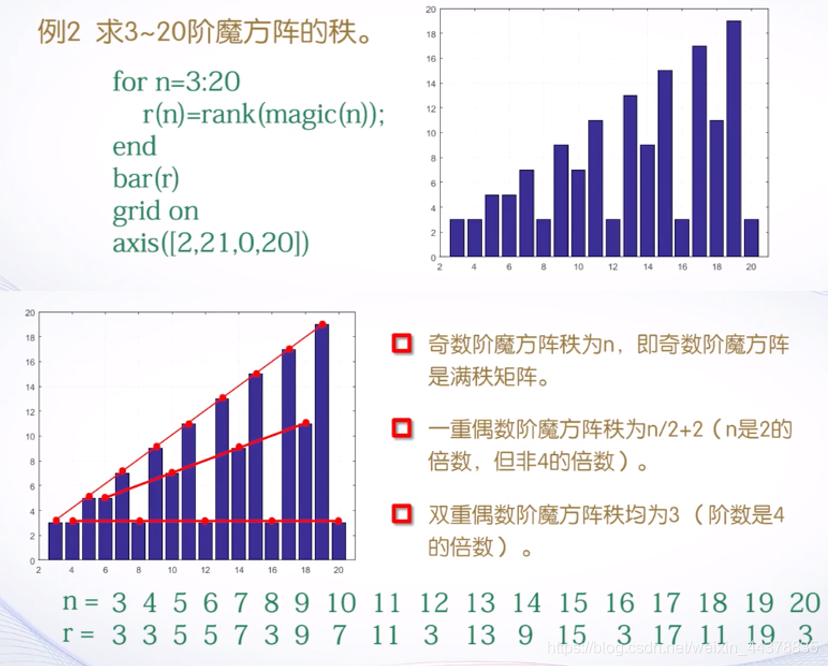
C.b 矩阵的秩

例题：

C.c 矩阵的迹

例子：

C.d 向量和矩阵的范数

矩阵或向量的范数用来度量矩阵或向量在某种意义下的长度。

C.e 矩阵的条件数

例题：

D 矩阵的特征值与特征向量

D.a 矩阵特征值的数学定义

D.b 求矩阵的特征值和特征向量

例子：A_X(:,1)=D(1)_X(:,1)

例题：

X3对角为X1和X2，

D.c 特征值的几何意义

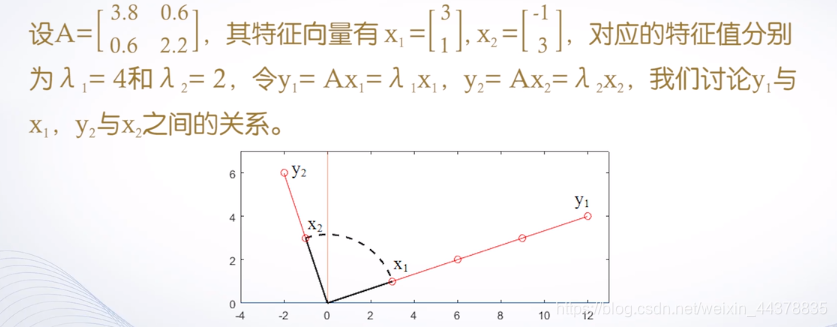
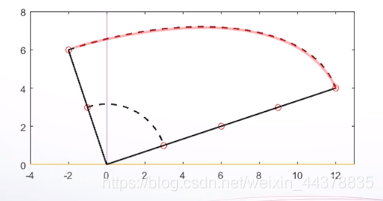
y1和y2分别是x1和x2经过A矩阵变换得到的。把当作伸缩因子，y1和y2是x1和x2经过伸缩以后的结果，如图所示。
更进一步地，连续取单位向量x，让它大小保持唯一，那么Ax就将圆弧拉伸，变成椭圆弧。

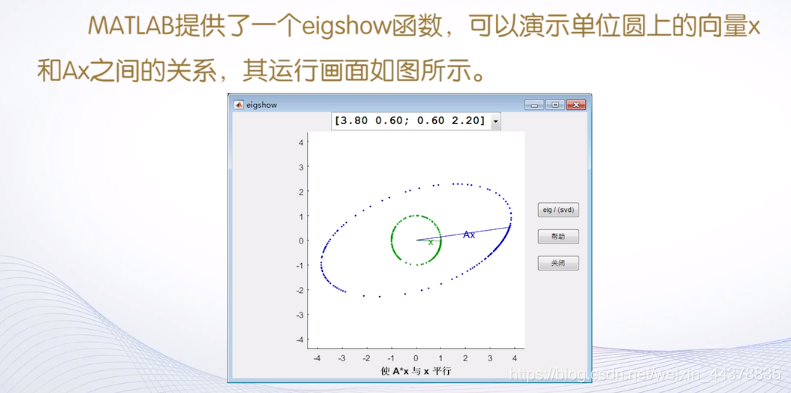
E 稀疏矩阵

稀疏矩阵指的是零元素个数远远多于非零元素个数的矩阵，如果将大量的零元素也存储起来，必将导致存储空间的浪费。为此，MATLAB为稀疏矩阵提供特殊的存储方式。

E.a矩阵的存储方式

例子：

E.b 稀疏存储方式的产生

例子：

例子：

用A的一行元素表示一个稀疏矩阵的元素，相当于A每一行的每个元素是相应的稀疏矩阵元素的一个信息。这些信息组合经过spconvert就可以得到相应的稀疏矩阵元素。
例子：
A描述的稀疏矩阵：[2，2，1：第二行第二列的1；2，1，-1：第二行第一列的-1；2，4，3：第二行第四列的3；其他为0。]经过spconvert实现A描述的稀疏矩阵。

例子：

A的稀疏存储：

E.c 稀疏矩阵应用举例

clc;clear
kf1= [1;1;2;1;0];     % 主对角线以下第一条元素
k0 = [2;4;6;6;1];     % 主对角线元素
k1 = [0;3;1;4;2];     % 主对角线以上第一条元素
B = [kf1,k0,k1];
d = [-1;0;1];
A = spdiags(B,d,5,5); % 产生稀疏存储的稀疏矩阵
f = [0;3;2;1;5];
x = A\f               %求出解

图片来源：
https://www.icourse163.org/search.htm?search=中南大学 Matlab#/