【Matlab】

[toc]

A 符号对象

A.a 符号对象的建立

• sym函数
• syms命令

<1> sym函数
sym函数用于建立单个符号对象，其常用调用格式为：符号对象名=sym(A)
将由A来建立符号对象。其中，A可以是一个数值常量、数值矩阵或数值表达式（不加单引号），此时符号对象为一个符号常量；A也可以是一个变量名（加单引号），这是符号对象为一个符号常量。

例子（符号常量）：

)#card=math&code=sin%28sym%28pi%2F3%29%29)得到的是一个表达式，而#card=math&code=sin%28pi%2F3%29)得到的是一个数值。
例子（符号变量）：

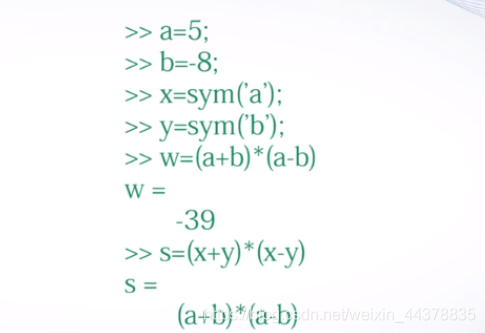
结论：符号计算的结果是一个精确的数学表达式。数值计算的结果是一个数值。

将符号表达式转化为数值结果，使用eval()

sym一次只能定义单个符号对象，如果符号对象很多，就不方便。

<2>syms命令
syms命令可以一次定义多个符号变量，其一般调用格式如下：
syms 符号变量1 符号变量2 ... 符号变量n
其中，变量名不能加单引号，相互之间用空格隔开。如：

建立完符号对象，再用符号运算符连接起来，就组成了符号表达式。

A.b 符号对象的运算

<1>四则运算
符号表达式的四则运算与数值运算一样，用+、-、*、/运算符实现，其运算结果依然是一个符号表达式。

<2>关系运算

• 6种关系运算符：<、<=、>、>=、==、~=。
• 对应的6个函数：lt()、le()、gt()、ge()、ge()、eq()、ne()。

若参与运算的是符号表达式，其结果是一个符号关系表达式；若参与运算的是符号矩阵，其结果是由符号关系表达式组成的矩阵。

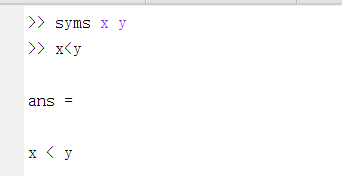
在进行符号对象的运算前，可用assume函数对符号对象设置域，函数调用格式为：
assume(condition)
assume(expr, set)

第一种格式指定变量满足条件condition，第二种格式指定表达式expr属于set

<3>逻辑运算

• 3种逻辑运算符：&(与)、|(或)和~(非)
• 4个逻辑运算函数：and()、or()、not()和xor()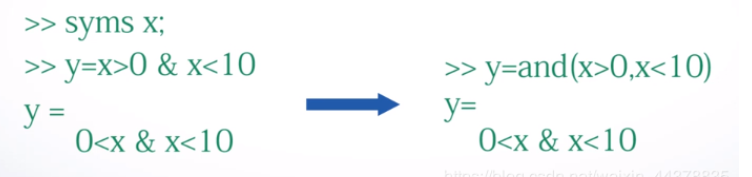
• 

<4>因式分解与展开运算
MATLAB提供了对符号表达式进行因式分解、展开、合并的函数，函数的调用格式为：
fator(s)：对符号表达式s分解因式。

expand(s)：对符号表达式s进行展开。
collect(s)：对符号表达式s合并同类项。
collect(s, v)：对符号表达式s按变量v合并同类项。

<5>其他计算

• 1 提取有理分式的分子分母：[n, d]=numden(s)
  
• 2 提取符号表达式的系数(低位到高位)：c=coeffs(s, x)
  
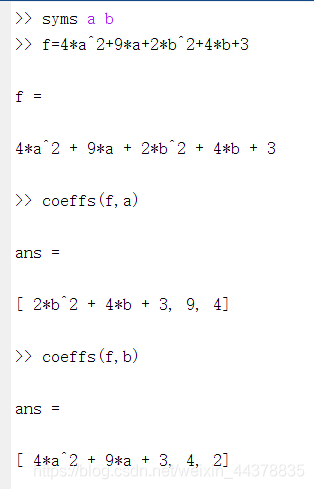
• 3 符号表达式化简：simplify(s)
• 4符号多项式与多项式系数向量之间的转换：
  符号多项式转换为多项式系数向量：p=sym2poly(s)
  多项式系数向量转换为符号多项式：s=ploy2sum()
  
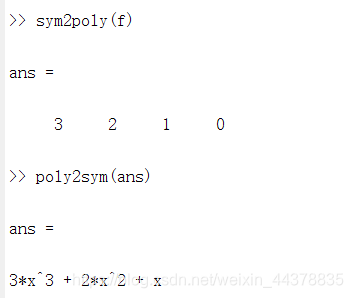
  f只能有一种符号变量

例子：

<6>符号运算中变量的确定

• 如果没有明确指定自变量，MATLAB将按以下原则确定主变量并对其进行相应运算：
  寻找除了i、j之外，在字母顺序上最接近x的小写字母。
  若表达式中有两个符号变量与x的距离相等，则ASCII码大者优先。

• symvar()函数可以用于查找一个符号表达式中的符号变量，函数的调用格式为：symvar(s,n)。函数返回符号符号表达式s中的n个符号变量。因此，可以用symvar(s, 1)查找表达式s的主变量。

A.c 符号矩阵

符号矩阵也是一种符号表达式，所以符号表达式运算都可以在矩阵意义下进行。
注意：这些函数作用于符号矩阵时，是分别作用于矩阵的每一个元素。

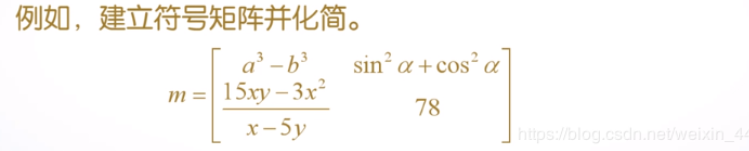
由于符号矩阵也是矩阵，所以有关矩阵的函数也可以使用。

B 符号微积分

B.a 符号函数的极限

<1>符号函数的极限

• 求符号函数极限的命令limit，其调用格式为：limit(f, X, a)即求函数f关于变量x在a点的极限。若x省略，则采用系统默认的自变量。a的默认值为0。
• limit函数的另一种功能是求单边极限，其调用格式为：
  limit(f, x, a, 'right')
limit(f,x,a,'left')

B.b 符号函数的导数

MATLAB中的求导函数为：diff(f, x, n)
即求函数f关于变量x的n阶导数。参数x的用法同求极限函数limit，可以缺省，默认值与limit相同，n的默认值是1。

极限、导数、微分的概念是紧密关联的。有极限是可导的前提，而导数是微分之商，因此导数也称为微商。

B.c 符号函数的积分

<1>不定积分

在MATLAB中，求不定积分的函数是int，其常用调用格式为：int(f, x)求函数f对变量x的不定积分。

<2>定积分
在MATLAB中，定积分的计算也使用int命令，但调用格式有区别：
int(f, a, b)
其中，a、b分别表示定积分的下限和上限。

• 当函数关于变量x在闭区间[a, b]可积时，函数返回一个定积分的结果。
• 当a、b中有一个是inf时，函数返回一个广义积分。
• 当a、b中有一个是符号表达式时，函数返回一个符号函数。

C 级数

C.a 级数求和

例子：


hypergeom:超几何函数

C.b 泰勒级数

例子：

D 符号方程求解

D.a 代数方程

例子：
solve所得到的结果可能不准确：

D.b 常微分方程

注意单引号。