数据结构：堆

  • 完全二叉树
  • parent >= children(大顶堆)、parent <= children(小顶堆)

堆排序平均时间复杂度：O(nlogn)

1-保证一个父节点是其子节点的最大值

完全二叉树可以由数组表示，坐标从0开始，对应树从上到下，从左往右

完全二叉树在数组中的特性，节点下标为 i，则：

  • 父节点在 (i - 1)/2 只保留整数部分
  • 左子节点 2i + 1
  • 右子节点 2i + 2

由此节点可构建一个小堆，这个过程可以称为 heapify

  1. public static void heapify(int[] tree, int length, int i) {
  2.     if (i >= length) {
  3.         return;
  4.     }
  5.     // 左子节点
  6.     int c1 = 2 * i + 1;
  7.     // 右子节点
  8.     int c2 = 2 * i + 2;
  9.     // 假设该父节点临时是最大值
  10.     int max = i;
  11.     // c1，c2 有可能不存在，也就是下标溢出
  12.     if (c1 < length && tree[c1] > tree[max]) {
  13.         max = c1;
  14.     }
  15.     if (c2 < length && tree[c2] > tree[max]) {
  16.         max = c2;
  17.     }
  18.     // 如果该父节点不是最大值，最大值与其交换位置，从而构建一个局部堆
  19.     if (max != i) {
  20.         swap(tree, i, max);
  21.     }
  22. }

2-将乱序完全二叉树构建成堆

从倒数第二层开始构建局部堆，由下至上，能够保证其子节点就是以下最大的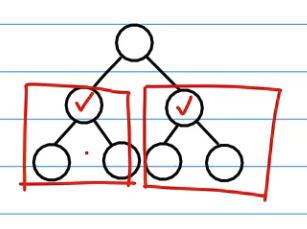
image.png
根据父节点的下标规律可知，某个父节点的上一个父节点在数组中的下标是 i—
由以上特性构建一个大顶堆

  1. public static void  buildHeap(int[] tree, int length) {
  2.     // 最后一个节点
  3.     int lastNode = length - 1;
  4.     // 最后一个父节点
  5.     int parent = (lastNode - 1) / 2;
  6.     while (parent >= 0) {
  7.         // 保证与其子节点构成堆结构
  8.         heapify(tree, length, parent);
  9.         // 上一个父节点是 index--
  10.         parent--;
  11.     }
  12. }

堆顶即当前堆的最大元素

3-堆顶与最后一个节点交换位置，截掉最后节点，重新构建堆

截取到最后一个节点，数组就有序了

  1. public static void heapSort(int[] tree) {
  2.     buildHeap(tree, tree.length);
  3.     for (int i = tree.length - 1; i >= 0; i--) {
  4.         swap(tree, i, 0);
  5.         buildHeap(tree, i);
  6.     }
  7. }

堆排序完整代码

  1. public class HeapSort {
  2.     public static void swap(int[] tree, int a, int b) {
  3.         int temp = tree[a];
  4.         tree[a] = tree[b];
  5.         tree[b] = temp;
  6.     }
  8.     public static void heapify(int[] tree, int length, int i) {
  9.         if (i >= length) {
  10.             return;
  11.         }
  12.         int c1 = 2 * i + 1;
  13.         int c2 = 2 * i + 2;
  14.         int max = i;
  15.         if (c1 < length && tree[c1] > tree[max]) {
  16.             max = c1;
  17.         }
  18.         if (c2 < length && tree[c2] > tree[max]) {
  19.             max = c2;
  20.         }
  21.         if (max != i) {
  22.             swap(tree, i, max);
  23.         }
  24.     }
  26.     public static void  buildHeap(int[] tree, int length) {
  27.         // 从最底层父节点 heapify，最底层父节点也是 index 最大的父节点，上一个父节点是 index--
  28.         int lastNode = length - 1;
  29.         int parent = (lastNode - 1) / 2;
  30.         while (parent >= 0) {
  31.             heapify(tree, length, parent);
  32.             parent--;
  33.         }
  34.     }
  36.     public static void heapSort(int[] tree) {
  37.         buildHeap(tree, tree.length);
  38.         for (int i = tree.length - 1; i >= 0; i--) {
  39.             swap(tree, i, 0);
  40.             buildHeap(tree, i);
  41.         }
  42.     }
  44.     public static void main(String[] args) {
  45.         int[] arr = {4, 9, 3, 5, 1, 2, 12, 5, 11, 44, 55, 13, 6};
  46.         HeapSort.heapSort(arr);
  47.         System.out.println(Arrays.toString(arr));
  48.     }
  50. }

满二叉树、完全二叉树、平衡二叉树、最优二叉树

满二叉树

一棵二叉树的结点要么是叶子结点，要么它有两个子结点
（如果一个二叉树的层数为K，且结点总数是(2^k) -1，则它就是满二叉树。）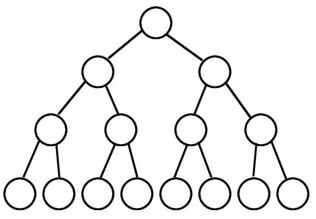
image.png

完全二叉树

若设二叉树的深度为k，除第 k 层外，其它各层 (1～k-1) 的结点数都达到最大个数，
第k 层所有的结点都 连续集中在最左边，这就是完全二叉树。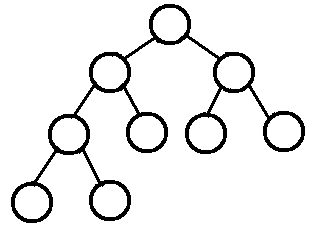
image.png

平衡二叉树

它或者是一颗空树，或它的左子树和右子树的深度之差(平衡因子)的绝对值不超过1，且它的左子树和右子树都是一颗平衡二叉树。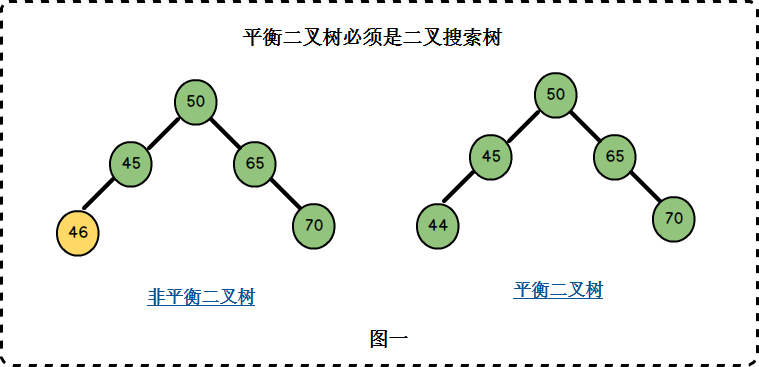
image.png

最优二叉树(哈夫曼树)

树的带权路径长度达到最小，称这样的二叉树为最优二叉树，也称为哈夫曼树(Huffman Tree)。哈夫曼树是带权路径长度最短的树，权值较大的结点离根较近。