我们在字符串 A 中查找字符串 B,那字符串 A 就是主串,字符串 B 就是模式串。我们把主串的长度记作 n,模式串的长度记作 m。因为我们是在主串中查找模式串,所以 n>m。
1.BF算法, Brute (暴力) Force(武力)
而且一般需要第一时间考虑的,因为肯定能解决问题.
主要思路就是 我们在主串中,检查起始位置分别是 0、1、2…n-m 且长度为 m 的 n-m+1 个子串,看有没有跟模式串匹配的。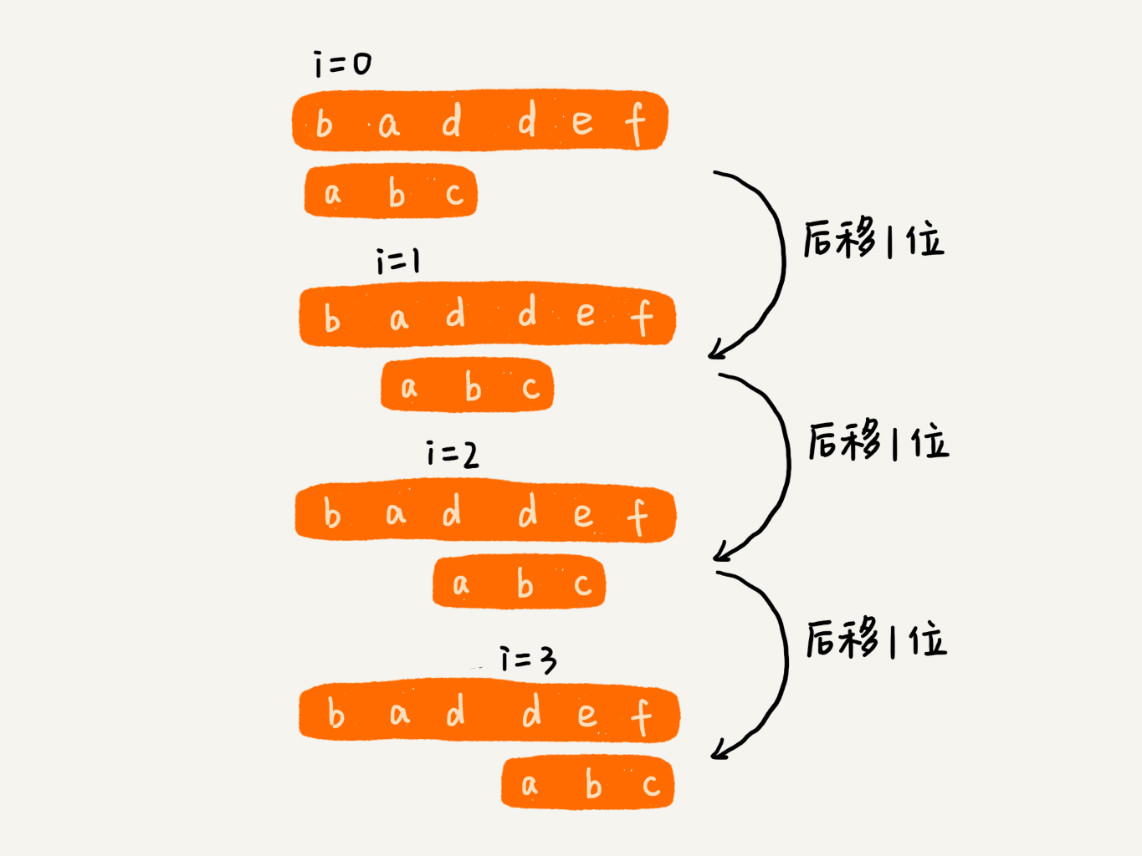
时间复杂度就是 O(n*m)
2.RK算法 Rabin-Karp (由它的两位发明者 Rabin 和 Karp 的名字来命名的)
主要思想就是运用哈希.(就不需要模式串一个一个匹配,可以打包匹配)
RK 算法的思路是这样的:我们通过哈希算法对主串中的 n-m+1 个子串分别求哈希值,然后逐个与模式串的哈希值比较大小。如果某个子串的哈希值与模式串相等,那就说明对应的子串和模式串匹配了(这里先不考虑哈希冲突的问题,后面我们会讲到)。因为哈希值是一个数字,数字之间比较是否相等是非常快速的,所以模式串和子串比较的效率就提高了。
同时会涉及到如何涉及哈希的问题,(哈希,将一段字符串使用一定的规则生成一串数字)
简单的来说,就可以使用 a-z 对应 1-26 ,然后相加,虽然会冲突,但是 再使用一个一个比较就好了.
1.遍历在主串中计算和模式串同样长度的的字符串的哈希值 ,这个时候会花O(n)的时间复杂度
2.然后模式串和这些子串比较,时间复杂度也是O(n)
3.BM算法(Boyer-Moore)算法 ,性能是KMP算法的3-4倍
坏字符策略:
BF算法的升级版本.主要思路是这样的 , 匹配的时候倒着顺序匹配,主串中匹配的最后一位 ,如果再模式串中不存在,然后说明整一串都不会存在,那么直接略过这一串. (都不存在了,肯定无法匹配)
如果存在,那么就把这个字符串进行对齐. 再来一次
好后缀策略:
是上面RK 的升级版 ,我就不计算哈希 ,我直接 用两个支付串去匹配.O(n)
如果匹配到了,那么我再把整个字符串移动过去进行全部匹配.
4.KMP算法,(目前还没完全看懂)
https://www.youtube.com/watch?v=dgPabAsTFa8

